【opencv-python】SeamCarving

SeamCarving中Seam的计算过程

• 给出能量矩阵，计算Seam

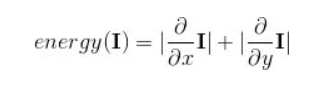
原理
给出能量矩阵，计算seam
能量矩阵：八联通，第一行值不变，从第二行开始找出能够到达该节点的最小和，采用动态规划，不断计算下一个值，直至最后一行。
实例
假设能量矩阵如下（深蓝色标记是已经计算的结果），
举例：对于第一个图到第二个图，5、8、12都与 2 是联通的，其中最小值为（5+2），故2 更新为 7，依此类推，如下：

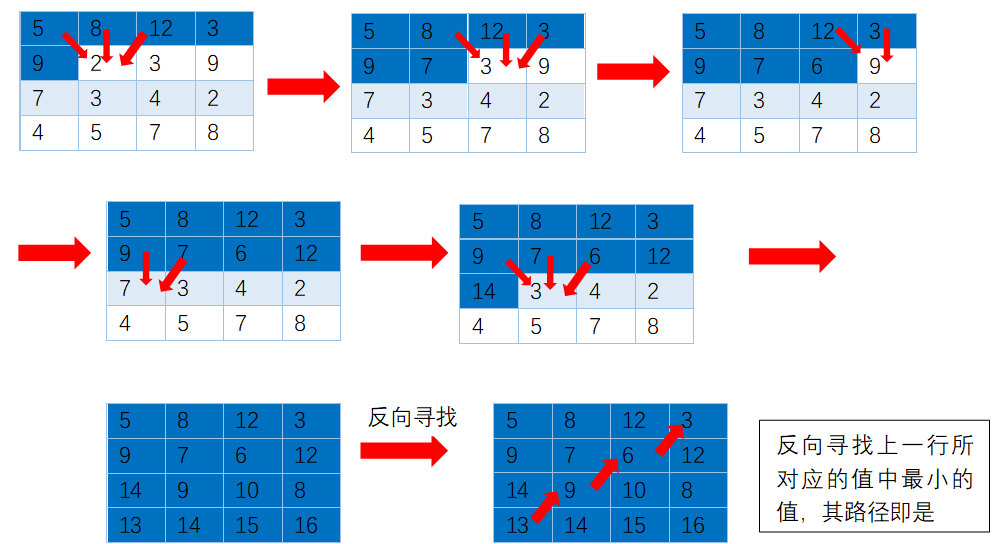
动态规划

import time

import cv2
import numpy as np


def energy_map(Image):
    """计算能量图"""
    # 对BGR三通道分别计算横向和纵向梯度值
    b, g, r = cv2.split(Image)
    b_energy = np.absolute(cv2.Sobel(b, -1, 1, 0)) + np.absolute(cv2.Sobel(b, -1, 0, 1))
    g_energy = np.absolute(cv2.Sobel(g, -1, 1, 0)) + np.absolute(cv2.Sobel(g, -1, 0, 1))
    r_energy = np.absolute(cv2.Sobel(r, -1, 1, 0)) + np.absolute(cv2.Sobel(r, -1, 0, 1))
    # 三通道相加得到能量值
    return b_energy + g_energy + r_energy


def find_seam(energy):
    """动态规划求最小能量值"""
    h, w = energy.shape
    seam = np.zeros(energy.shape)
    for i in range(1, h):
        for j in range(0, w):
            if j == 0:
                min_index = np.argmin(energy[i - 1, j:j + 1]) + j
                energy[i, j] += int(energy[i - 1, min_index])
                seam[i, j] = min_index
            else:
                min_index = np.argmin(energy[i - 1, j - 1:j + 1]) + j - 1
                energy[i, j] += int(energy[i - 1, min_index])
                seam[i, j] = min_index
    # 返回路径
    return energy, seam


def delete_seam(Image, seam, Energy):
    h, w, _ = Image.shape
    output = np.zeros((h, w - 1, 3))
    # 回溯求路径
    j = np.argmin(Energy[-1])
    for i in range(h - 1, 0, -1):
        for k in range(3):
            output[i, :, k] = np.delete(Image[i, :, k], [j])    # 逐行删除对应能量值最小的像素点
            j = int(seam[i][j])
    return output


def seam_carving(Image, delta):
    """
    循环多次剪切
    :param Image:
    :param delta: 删除的像素条数
    :return:
    """
    time_start = time.time()
    for t in range(delta):
        energy = energy_map(Image)
        Energy, seam = find_seam(energy)
        Image = delete_seam(Image, seam, Energy)
        print(delta - t)
    time_end = time.time()
    print('time cost:', time_end - time_start, 's')
    return Image


if __name__ == '__main__':
    image = cv2.imread('imgs/kangna.jpg')
    E = energy_map(image)
    cv2.imwrite('energy.jpg', E)
    output_image = seam_carving(image, 300)
    cv2.imwrite('cut_image.jpg', output_image)

最后

以上就是动人书本为你收集整理的【opencv-python】SeamCarving的全部内容，希望文章能够帮你解决【opencv-python】SeamCarving所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。