DFT圆周对称性

将DFS排列在$0\le n\le N-1$的圆周上,序列是关于圆周对称的.所以得到的DFS前$\frac{N}{2}$项表示区间$[0,\frac{fs}{2}]$上的频率分量,而后$\frac{N}{2}$项表示区间$[-\frac{fs}{2},0]$上的频率分量.

DFT圆周对称性的根本原因来自于实序列DTFT的对称性

实序列的Fourier变换$X(e^{j\omega })$满足共轭对称性
$$X(e^{j\omega })=X^{\ast }(e^{-j\omega })$$
也就是说,$X(e^{j\omega })$的
实部满足偶对称关系,虚部满足奇对称关系
模满足偶对称关系,相位满足奇对称关系

DFT后横轴的量纲

我们在对有限长采样序列进行DFT后，得到的是一组无量纲的DFS系数，所以现在问题就在于如何关联到频率，进行频率分析.
对于周期信号,一个周期内的相移为$2\pi$,将一个周期分为N个采样点,那么相邻两个点之间应该有相位差$\frac{2\pi }{N}$,采样时间为$\frac{1}{f_s}$,所以可知两采样点频率间隔为$\frac{f_s}{N}$.
其他解释

频率分辨率

DFT可认为是对DTFT主值周期的抽样，而抽样的间隔正是两采样点频率间隔为$\frac{f_s}{N}$,因此频谱会存在一个最小分辨间距，若两个频率分量的峰值小于这个间距，则不能被识别.

频谱混叠失真

当抽样频率f_s不满足抽样定理时,频域的周期延拓会产生混叠,导致频谱的混叠失真.
在选择f_s时,应保证$f\le \frac{f_s}{2}$内包含98%的能量,在$f_s=(3\sim 6)f_h$内选择.

频谱泄露

时域相乘，频域卷积.在对时域截短近似时,可视作原序列与窗函数相乘,由于窗函数频谱的特性,原序列的频谱将发生非线性变化(产生新的频谱分量)

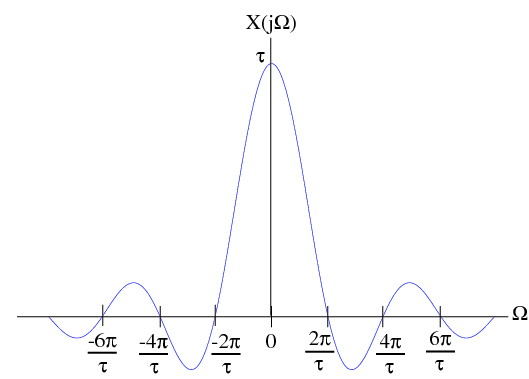
频谱泄露将产生一下几点问题

1. 谱线展宽，降低频率分辨率
   以正弦型函数为例，频谱应当为脉冲，但实际截短后，频谱能量主要分布在矩形窗频谱的主瓣内，相当于使原来的频谱展宽.因此,当两频率分量相隔小于主瓣宽度的一半$\frac{2\pi }{\tau }$,由于频谱泄露，导致叠加后不能分辨.
   所以,矩形窗的主瓣宽度决定了相邻频率的分辨能力,因而将主瓣宽度的一半定义为矩形窗的频率分辨率
   $$\Delta f=\frac{1}{N}$$
2. 谱间串扰
   由于截短后产生很多旁瓣，可能使强信号的旁瓣掩盖弱信号的主瓣，降低分辨率

为了减轻截断效应，可以

1. 采用缓变型窗函数，使旁瓣快速衰减
2. 增加取样点数N，使主瓣更窄

栅栏效应

在用DFT进行频谱分析时，根据上文可知，得到的频谱是有分辨率的，也就是说，我们实际看到的只是连续频谱的相隔$\frac{f_s}{N}$的抽样,在抽样点外的信息我们是看不见的.
为了减小栅栏效应,可以

1. 在数据长度不变(截取时间不变)的情况下,增加采样频率，获得更多的采样点数.
2. 在有效数据中补零,增加DFT的计算点数.

关于高密度谱与高分辨谱的说明：
高密度谱:频域一个周期内计算点数更多，从而使频谱更加平滑.
高分辨谱:拥有更高的分辨能力,通常对应更多的采样点数
虽然补零后使一个周期内的点数增加，样点间隔更近，但是补零比没有添加有用的信息，所以补零不能提高分辨率.
通俗一点说,把64点补成256点 和 128点补成256点,虽然点数一样了，能看见绝对不一样,而且64点看不到的补成512点还是看不到,但是它两看起来都很圆润.
增加频谱分辨率的唯一方法只有增加采样点数N

最后

以上就是高挑小蘑菇为你收集整理的DFT对模拟信号作频谱分析出现的问题DFT圆周对称性DFT后横轴的量纲频率分辨率频谱混叠失真频谱泄露栅栏效应的全部内容，希望文章能够帮你解决DFT对模拟信号作频谱分析出现的问题DFT圆周对称性DFT后横轴的量纲频率分辨率频谱混叠失真频谱泄露栅栏效应所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。