基于粒子群算法(PSO)的PID参数优化(源代码+详细注释—小白入门)
【无需积分哦!第一次发帖,纰漏之处还请谅解。另外,本文附带所有文件会在下一个博客发出(第一次发帖,不知道附件总么一同上传)】
链接: link.https://download.csdn.net/download/meyyyy/16623575
一、pso原理
二、matlab的.m程序实现
三、pos算法检验
本文分三部分讲解:pso原理+matlab的.m程序实现+验证
(前序知识:离散化的增量式pid原理及其matlab函数的实现。注:程序块(二)运用到增量式pid)
一、pso原理(智能控制里比较简单的一个算法)
一、pso原理(智能控制里比较简单的一个算法)




二、matlab的.m程序实现
程序块(一)
%基于PSO算法的PID参数优化
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口
%% 参数设置
w = 0.6; % 惯性因子 (0~1之间,不宜过大或过小)
c1 = 2; % 加速常数
c2 = 2; % 加速常数
Dim = 3; % 维数
SwarmSize =100; % 粒子群规模
MaxIter = 100; % 最大迭代次数
MinFit = 0.1; % 最小适应值
Vmax = 1;
Vmin = -1;%对速度范围进行限制
Ub = [50 50 50];
Lb = [0 0 0];%对位置进行限制
%% 粒子群初始化(每个粒子的位置和速度都是一个1行3列的矩阵,共100个粒子
%即整体的位置和速度均为为100行3列的矩阵 )
Range = ones(SwarmSize,1)*(Ub-Lb);%100行1列 乘以 1行3列得 100行3列元素均为50的矩阵
Swarm = rand(SwarmSize,Dim).*Range + ones(SwarmSize,1)*Lb; % 初始化粒子群(是一个位置信息100行3列)
%内部元素均为0~50之间
VStep = rand(SwarmSize,Dim)*(Vmax-Vmin) + Vmin; % 初始化速度(100行3列,每个元素在-1~1之间)
%矩阵加常值默认为每个元素都加Vmin
%亦可为VStep = rand(SwarmSize,Dim)*(Vmax-Vmin) +ones(SwarmSize,Dim)* Vmin;
fSwarm = zeros(SwarmSize,1);%产生一个元素均为0得100行1列得矩阵
%可认为为“空”矩阵,用于存放后续迭代得到的100个粒子的适应值
for i=1:SwarmSize%依次求出每个粒子的适应值
fSwarm(i,:) = pid_pso(Swarm(i,:)); % 粒子群的适应值
%此适应度函数由另一个文件编写,也可以和该程序合为一个程序
end
%% 个体极值和群体极值
[bestf,bestindex]=min(fSwarm);%fswarm中每列最小元素为bestf,最小元素的位置为(每列由上到下)bestindex)
%fswarm为100行1列的矩阵,bestindex属于0~100,即第bestindex个粒子经过100次迭代取得全局最小适应度值bestf;
zbest=Swarm(bestindex,:); % 全局最佳。100个粒子经过100次迭代,第bestindex个粒子(fSwarm值最小)对应位置,3行1列。
gbest=Swarm; % 个体最佳。第一个最佳值由初始化随机产生,若后来迭代出有更小值,用该值取代之。
%第i个粒子经过100次迭代中使第i个粒子适应值最小的位置。(只和自己适应值比较,不和其他99个比较)
fgbest=fSwarm; % 个体最佳适应值。100个粒子经过100次迭代,每,100行1列
fzbest=bestf; % 全局最佳适应值。100个粒子产生各自的最小适应值中再比较选出全局最小适应值
%(需要知道那个粒子(第bestindex个)对应该全局最小适应值及该粒子对应位置信息(zbest))
%% 迭代寻优
iter = 0;%第零次迭代(未迭代)
y_fitness = zeros(1,MaxIter); % 本行及以下3行预先产生4个“空”(元素为零)矩阵(1列100行)
K_p = zeros(1,MaxIter); %用于放100次迭代产生的前全局最佳位置对应的三维行向量第一个值
K_i = zeros(1,MaxIter);%用于放100次迭代产生的前全局最佳位置对应的三维行向量第二个值
K_d = zeros(1,MaxIter);%用于放100次迭代产生的前全局最佳位置对应的三维行向量第三个值
while( (iter < MaxIter) && (fzbest > MinFit) )%迭代次数不到100次并且全局最佳值(指适应度值)大于0.1才执行。否则跳出循环。
for j=1:SwarmSize%对100个粒子,每一次迭代依次对每个粒子的位置、速度、适应值进行更新
% 速度更新
VStep(j,:) = w*VStep(j,:) + c1*rand*(gbest(j,:) - Swarm(j,:)) + c2*rand*(zbest - Swarm(j,:));
%rand-等概率的产生一个0~1之间的数(以增加对个体最佳和全局最佳的搜索)
if VStep(j,:)>Vmax, VStep(j,:)=Vmax; end%若第j个粒子速度超过最大速度,令该粒子速度等于最大速度
if VStep(j,:)<Vmin, VStep(j,:)=Vmin; end%若第j个粒子速度低于最小速度,令该粒子速度等于最小速度
% 位置更新
Swarm(j,:)=Swarm(j,:)+VStep(j,:);%位置为什么等于先前位置加速度而不是加VStep(j,:)*T呢?
%可以这样理解:间隔迭代时间为T(这个T理解为单位时间,同现实中单位时间为1s含义一样,只不过T不等于1s)
%每个粒子每隔T走一步(一步一迭代),即单位时间内走一步,所以距离等于速度(值得注意的是粒子速度是阶跃的,阶跃的距离是随机的)
for k=1:Dim
if Swarm(j,k)>Ub(k), Swarm(j,k)=Ub(k); end%若第j个粒子位置超过最大位置边界值,令该粒子位置等于最大位置边界值
if Swarm(j,k)<Lb(k), Swarm(j,k)=Lb(k); end%若第j个粒子位置低于最小位置边界值,令该粒子位置等于最小位置边界值
end
% 适应值
fSwarm(j,:) =pid_pso(Swarm(j,:));
% 个体最优更新
if fSwarm(j) < fgbest(j)%若第j个粒子当前适应值小于先前个体最佳适应值
gbest(j,:) = Swarm(j,:);%令第j个粒子位置取代先前个体最佳位置(gbest(j,:) 用于“个体”记录位置信息,当这个“个体”取得全局最佳时,gbest(j,:)就给了 zbest )
fgbest(j) = fSwarm(j);%则令j个粒子当前适应值取代先前个体最佳适应值成为新的个体最佳适应值,否则先前个体最佳适应值不变(不断寻“小”的过程)
end
% 群体最优更新
if fSwarm(j) < fzbest%再已迭代步数的粒子中(每一次迭代,100个粒子的速度、位置、适应值fSwarm(j) 同时变化,fSwarm(j)与先前全局最佳适应值作比较 )
%若第j个粒子当前适应值小于先前全局最佳适应值
zbest = Swarm(j,:);%令第j个粒子位置取代先前全局最佳位置
fzbest = fSwarm(j);%则令j个粒子当前适应值取代先前全局最佳适应值成为新的全局最佳适应值,否则先前全局最佳适应值不变
end %%%要强调的是:第j个粒子当前适应值既要和 先前个体最佳适应值 作比较,又要和 先前全局最佳适应值 作比较。以保证全局最佳和个体最佳为“真”
end
iter = iter+1; % 迭代次数更新
y_fitness(1,iter) = fzbest; % 为绘图做准备 每一次迭代更新的fzbest(100个值)存放在 y_fitness(1,iter) (1行iter列)中,运行完毕后 y_fitness为1行100列
%zbest记录,每一步产生一个三维行向量。100步运行完毕后产生100行3列矩阵(100个3维向量)
K_p(1,iter) = zbest(1); %每一步当前全局最佳位置对应的三维向量(行向量)的第一个值给 K_p(1,iter) , 整体的K_p(1,iter)描述了zbest第一列元素的跨度
K_i(1,iter) = zbest(2);%每一步当前全局最佳位置对应的三维向量(行向量)的第二个值给 K_i(1,iter) ,整体的K_i(1,iter)描述了zbest第二列元素的跨度
K_d(1,iter) = zbest(3);%每一步当前全局最佳位置对应的三维向量(行向量)的第一个值给 K_d(1,iter) ,整体的K_p(1,iter)描述了zbest第三列元素的跨度
end
%%绘图
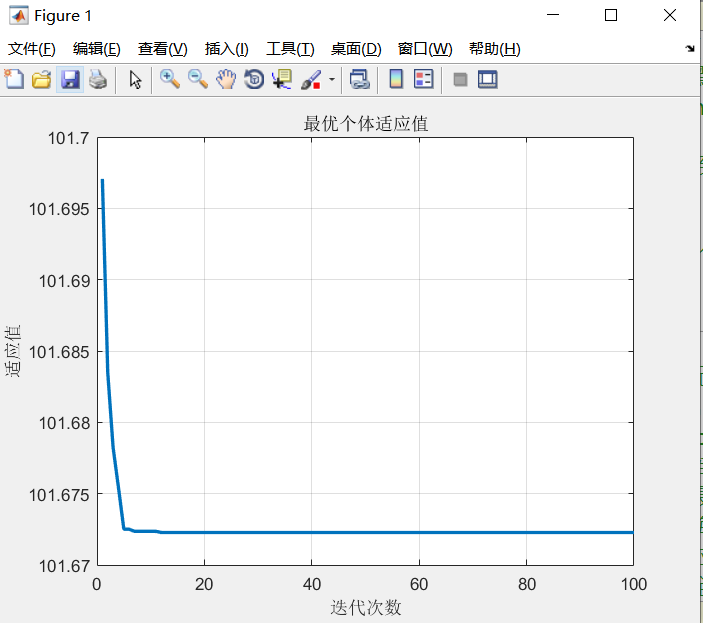
figure(1) % 绘制性能指标ITAE的变化曲线
plot(y_fitness,'LineWidth',2)
title('最优个体适应值','fontsize',10);
xlabel('迭代次数','fontsize',10);ylabel('适应值','fontsize',10);
set(gca,'Fontsize',10);
grid on
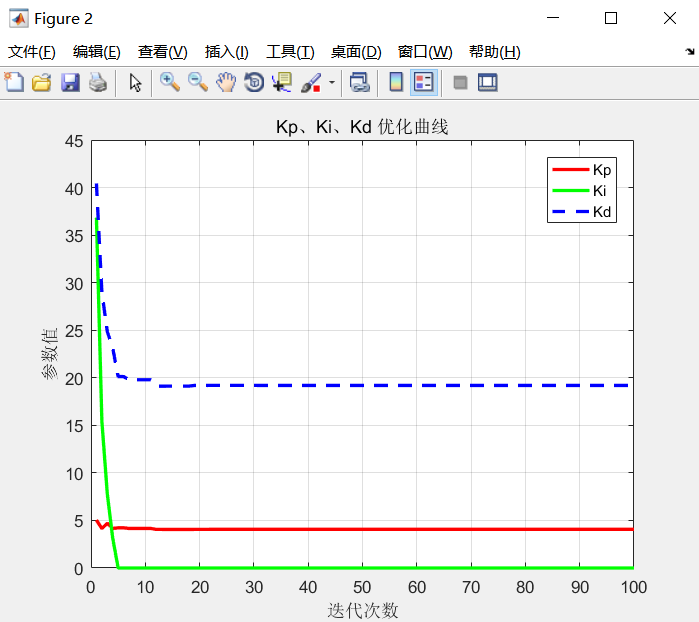
figure(2) % 绘制PID控制器参数变化曲线
plot(K_p,'r','LineWidth',2)
hold on
plot(K_i,'g','LineWidth',2)
plot(K_d,'--b','LineWidth',2)
title('Kp、Ki、Kd 优化曲线','fontsize',10);
xlabel('迭代次数','fontsize',10);ylabel('参数值','fontsize',10);
set(gca,'Fontsize',10);
legend('Kp','Ki','Kd');
grid on
save kpid.mat K_p K_i K_d
程序块(2)
(结合程序(1)使用,两个程序块分两个.m文件储存)
function BsJ=pid_pso(Kpidi)
ts=0.001;
sys=tf([1.6],[1 1.5 1.6],'inputdelay',0.1);
dsys=c2d(sys,ts,'z');
[num,den]=tfdata(dsys,'v');
u_1=0.0;u_2=0.0;
y_1=0.0;y_2=0.0;
x=[0,0,0]';
B=0;
error_1=0;
tu=1;
s=0;
P=100;
for k=1:1:P
timef(k)=k*ts;
r(k)=1;
u(k)=Kpidi(1)*x(1)+Kpidi(2)*x(3)+Kpidi(3)*x(2);
if u(k)>=10
u(k)=10;
end
if u(k)<=-10
u(k)=-10;
end
yout(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2;
error(k)=r(k)-yout(k);
%Return of PID parameters
u_2=u_1;u_1=u(k);
y_2=y_1;y_1=yout(k);
x(1)=error(k); % Calculating P
x(2)=(error(k)-error_1)/ts; % D
x(3)=x(3)+error(k)*ts; % I
error_2=error_1;
error_1=error(k);
if s==0
if yout(k)>0.95&yout(k)<1.05
tu=timef(k);
s=1;
end
end
end
for i=1:1:P
Ji(i)=0.999*abs(error(i))+0.01*u(i)^2*0.1;
B=B+Ji(i);
if i>1
erry(i)=yout(i)-yout(i-1);
if erry(i)<0
B=B+100*abs(erry(i));
end
end
end
BsJ=B+0.2*tu*10;
程序块(1)输出波形
三、pos算法检验(自建simulink模型)
模型一(在被控对象输入处给阶跃扰动,误差验证,如下图)
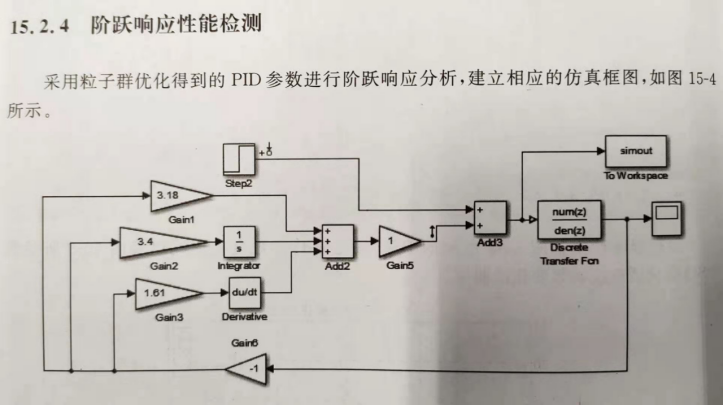
模型一输出误差曲线如下图
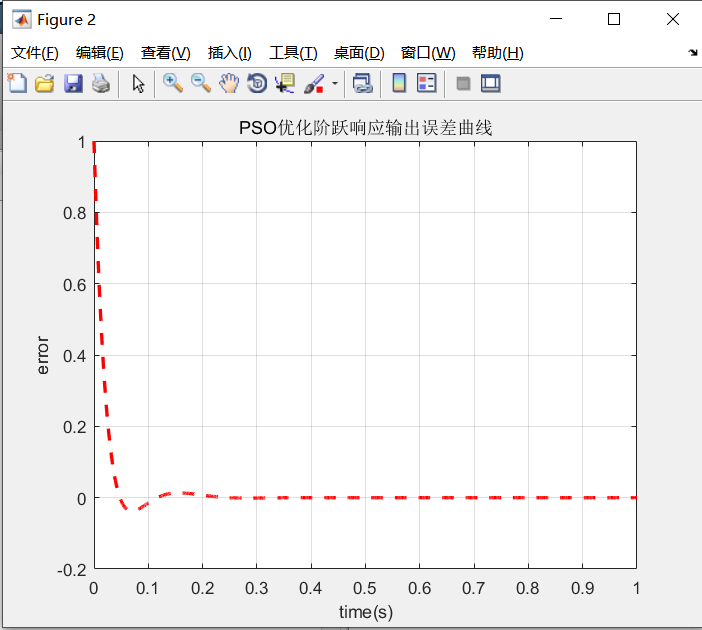
模型二(阶跃响应输入,验证误差及输出响应,如下图)
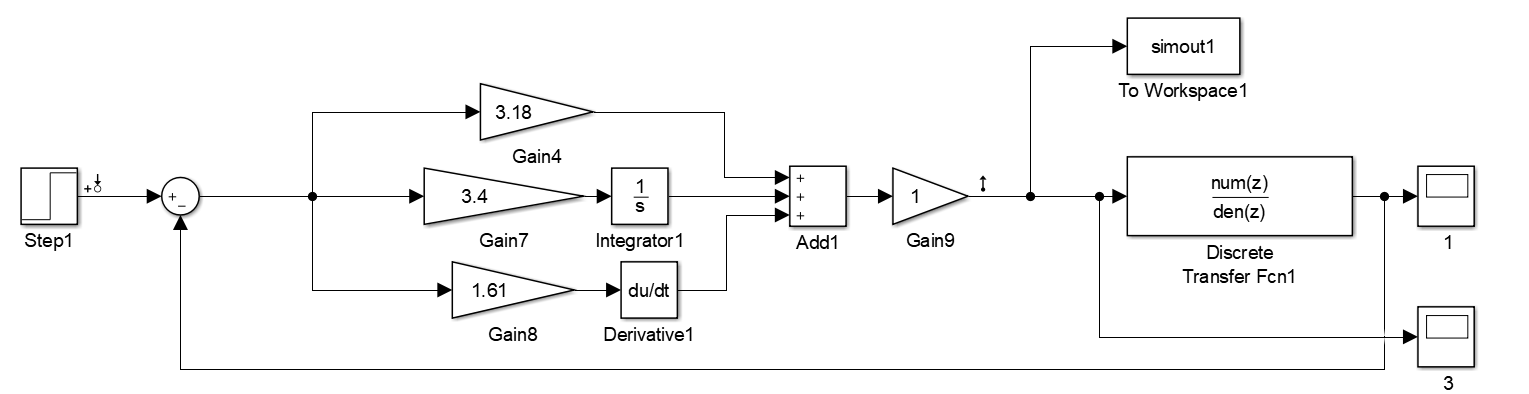
Discrete Transfer Fcn 为闭环传递函数G1(S),前文已给出。模型二输出误差
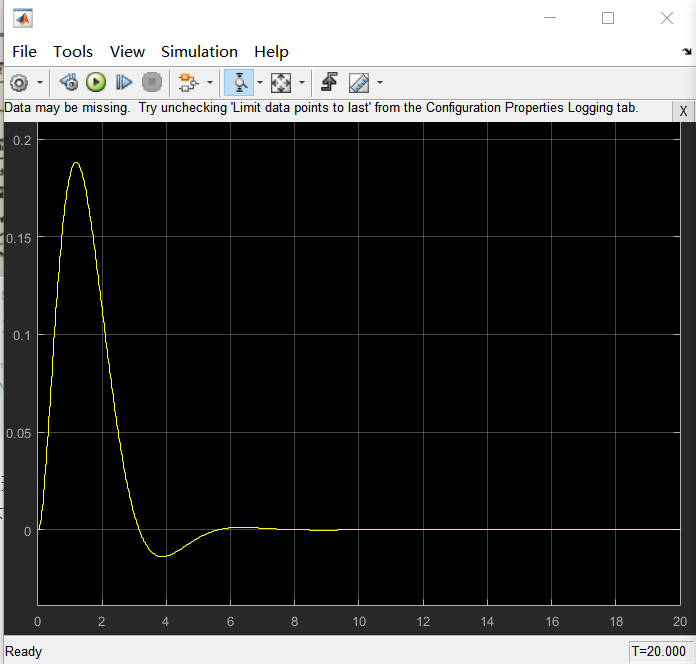
以上误差曲线(1.6秒后)与模型一误差输出曲线走势基本一致
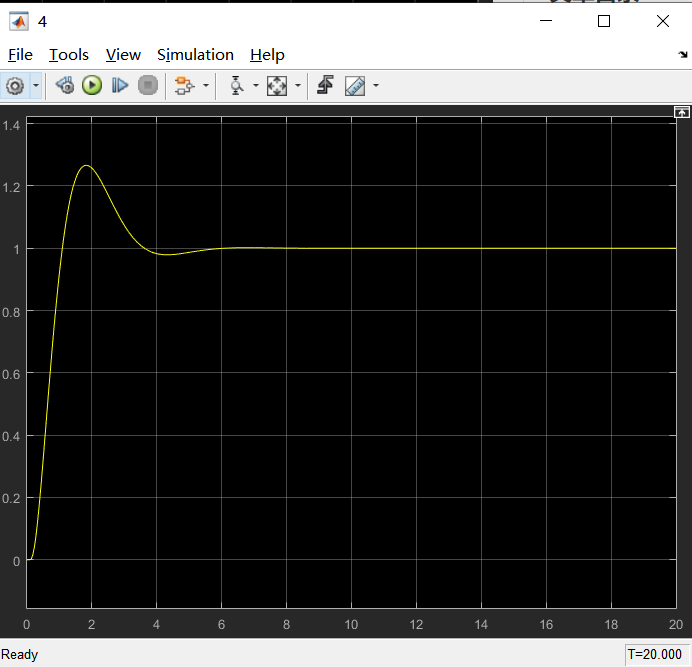
以上阶跃响应曲线
输出波形说明pso优化的pid控制系统稳定性较好。运用:如电机控制中,常用的比如滞环、foc、dtc控制,pi控制器参数可以用pso寻优,省去繁琐的计算过程。
最后
以上就是悲凉酸奶最近收集整理的关于2021-04-11基于粒子群算法(PSO)的PID参数优化(源代码+详细注释—小白入门)的全部内容,更多相关2021-04-11基于粒子群算法(PSO)内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复