机器学习之Softmax（Matlab仿真）

69 阅读 0 评论 46 点赞

我是靠谱客的博主健康皮带，最近开发中收集的这篇文章主要介绍机器学习之Softmax（Matlab仿真），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

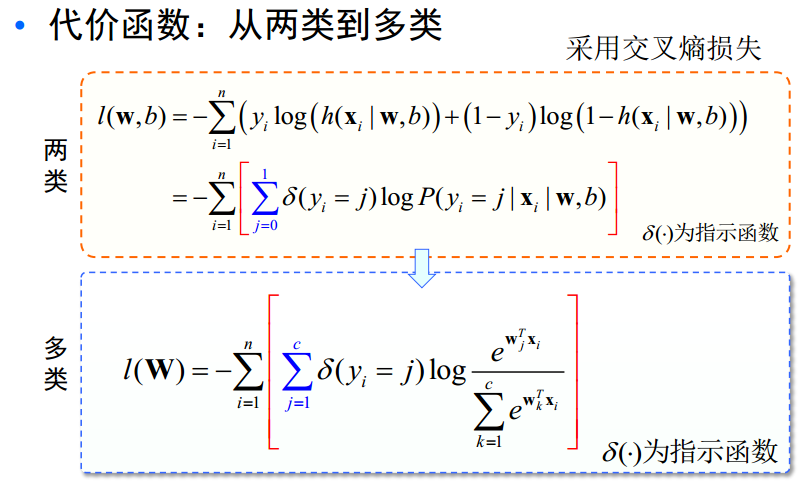
在这里插入图片描述

首先，使用 Matlab 生成如下数据集：

Sigma = [1, 0; 0, 1];
mu1 = [1, -1];
x1 = mvnrnd(mu1, Sigma, 200);
mu2 = [5, -4];
x2 = mvnrnd(mu2, Sigma, 200);
mu3 = [1, 4];
x3 = mvnrnd(mu3, Sigma, 200);
mu4 = [6, 4.5];
x4 = mvnrnd(mu4, Sigma, 200);
mu5 = [7.5, 0.0];
x5 = mvnrnd(mu5, Sigma, 200);
% Show the data points
plot(x1(:,1), x1(:,2), 'r.'); hold on;
plot(x2(:,1), x2(:,2), 'b.');
plot(x3(:,1), x3(:,2), 'k.');
plot(x4(:,1), x4(:,2), 'g.');
plot(x5(:,1), x5(:,2), 'm.');

生成的图像如下：

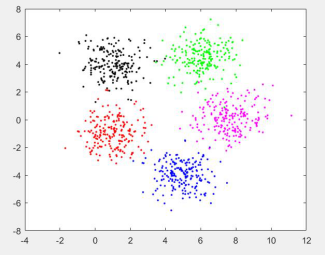
现在假定 x1 中的 200 个点属于第一类， x2 中的 200 个点属于第二类， x3 中的 200 个点属于第三类， x4 中的 200 个点属于第四类， x5 中的 200 个点属于第五类。请编写一个 Matlab 程序，采用正则化 softmax 回归方法来实现分类。

因为共有五类输出，设计参数theta矩阵有（5-1）*3=12个元素，初始化为均值为1，方差为1的随机数。根据学习模型建立损失函数和梯度函数。值得注意的是，图片中的梯度更新应直接加在原梯度上，而不能用减号！（这个坑我花了半天才发现）
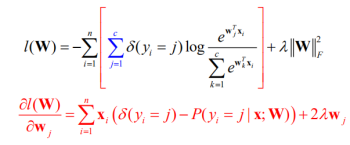
在这里插入图片描述
本次仿真中，Lambda值为1e-4，learning rate值为1e-3。每更新10万次，learning rate会减小至原来幅值的0.1。当循环到梯度的二范数小于0.001时停止。最终训练出来的损失函数值为15，测试集的正确率为98%，此时theta参数如下：
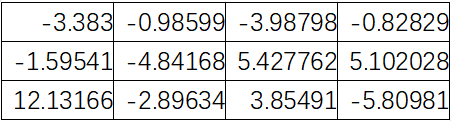
在这里插入图片描述
附代码：

Sigma = [1,0; 0,1];  %协方差，互不相关
mu1 = [1, -1];
x1 = mvnrnd(mu1, Sigma, 200);  %多元随机正态分布
mu2 = [5, -4];
x2 = mvnrnd(mu2, Sigma, 200);
mu3 = [1, 4];
x3 = mvnrnd(mu3, Sigma, 200);
mu4 = [6, 4.5];
x4 = mvnrnd(mu4, Sigma, 200);
mu5 = [7.5, 0.0];
x5 = mvnrnd(mu5, Sigma, 200);
 
lambda = 1e-4;
learning_rate = 0.001;
 
%显示数据点
plot(x1(:,1), x1(:,2), 'r.');hold on;
plot(x2(:,1), x2(:,2), 'b.');
plot(x3(:,1), x3(:,2), 'k.');
plot(x4(:,1), x4(:,2), 'g.');
plot(x5(:,1), x5(:,2), 'm.');
 
%划分测试集和训练集
x1_train = x1(1:120,:)';
x1_train(3, :) = 1;
x1_test = x1(121:200,:)';
x1_test(3, :) = 1;
 
x2_train = x2(1:120,:)';
x2_train(3, :) = 1;
x2_test = x2(121:200,:)';
x2_test(3, :) = 1;
 
x3_train = x3(1:120,:)';
x3_train(3, :) = 1;
x3_test = x3(121:200,:)';
x3_test(3, :) = 1;
 
x4_train = x4(1:120,:)';
x4_train(3, :) = 1;
x4_test = x4(121:200,:)';
x4_test(3, :) = 1;
 
x5_train = x5(1:120,:)';
x5_train(3, :) = 1;
x5_test = x5(121:200,:)';
x5_test(3, :) = 1;
 
train_set = [x1_train, x2_train, x3_train, x4_train, x5_train];
%train_set = cat(3, x1_train, x2_train, x3_train, x4_train, x5_train);
test_set = [x1_test, x2_test, x3_test, x4_test, x5_test];
 
%分类
A =  zeros(5, 600);
A(1, 1:120) = 1;
A(2, 121:240) = 1;
A(3, 241:360) = 1;
A(4, 361:480) = 1;
A(5, 481:600) = 1;
 
T = zeros(5, 400);
T(1, 1:80) = 1;
T(2, 81:160) = 1;
T(3, 161:240) = 1;
T(4, 241:320) = 1;
T(5, 321:400) = 1;
 
%定义参数θ
theta = mvnrnd([1,1], Sigma, 4)';
theta(3, :) = 0;
 
%梯度下降
gradient = ones(size(theta));
i = 0;
while sum(gradient(:) .^ 2) >= 0.001
    i = i+1;
    b=theta' * train_set;
    b(size(b,1)+1,:)=0;
    a=exp(b);
    sum_col = sum(a);
    P=bsxfun(@rdivide,a,sum_col);
 
    P_log = log(P);
    loss = -sum(sum(P_log.*A)) + lambda/2 * sum(theta(:) .^ 2);
    %fprintf('%fn', loss)
    %梯度
    gradient = 1/20. * train_set * (A(1:4, :) - P(1:4, :))' + lambda*theta;
    theta = theta + learning_rate * gradient * (0.1^floor(i/100000)) ;
end
 
fprintf('训练集交叉损失熵为：%3dn', loss);
lines = bsxfun(@rdivide,theta(2:3 ,:),-theta(1, :));
for i = 1:4
    refline(lines(1, i), lines(2, i));
end
 
%测试
y = theta'* test_set;
y(5, :) = 0;
y = exp(y);
P_test = bsxfun(@rdivide,y,sum(y));
[v, location] = max(P_test);
I = sub2ind(size(P_test), location, 1:size(test_set, 2));
B = zeros(size(P_test));
B(I) = 1;
AC = sum(sum(B.*T)) / 400;
fprintf('测试集正确率为：%3dn', AC);