研究项目
模糊PID(Fuzzy)的仿真测试
研究内容
本篇文章主要研究如何通过matlab软件实现模糊PID(Fuzzy)的仿真测试。
研究材料
- matlab 2017a软件
- 基本概念和定义
- 模糊量:如E、EC;
- 论域(上下限):-240~240;
- 划分区间:-240 ~ -180;-180 ~ -120 ;-120 ~ -60;-60 ~ 0;0 ~ 60;60 ~ 120;120 ~ 180;180 ~ 240;
- 隶属度:隶属于某个模糊子集的隶属度,程度;
- 模糊子集:
- 负大NB(Negative Big)
- 负中NM(NegativeMedium)
- 负小NS(NegativeSmall)
- 零ZE或ZO(Zero)
- 正小PS(PositiveSmall)
- 正中PM(PositiveMedium)
- 正大PB(Positive Big)
- 隶属度函数:用于求解隶属度,有线性的、非线性的。
研究方法
利用matlab模糊控制工具箱为模糊控制的设计提供了一种非常便捷的途径,通过它我们不需要进行复杂的模糊化、模糊推理及反模糊化运算,只需要设定相应的参数,就可以很快得到我们所需要的控制器,而且修改也非常方便。下面将根据模糊控制器设计步骤,一步一步利用Matlab工具箱设计模糊控制器。
-
模糊控制工具箱使用
首先我们在Matlab的命令窗口(command window)中输入“fuzzy”,回车就会弹出fuzzy模糊控制器窗口(window)。
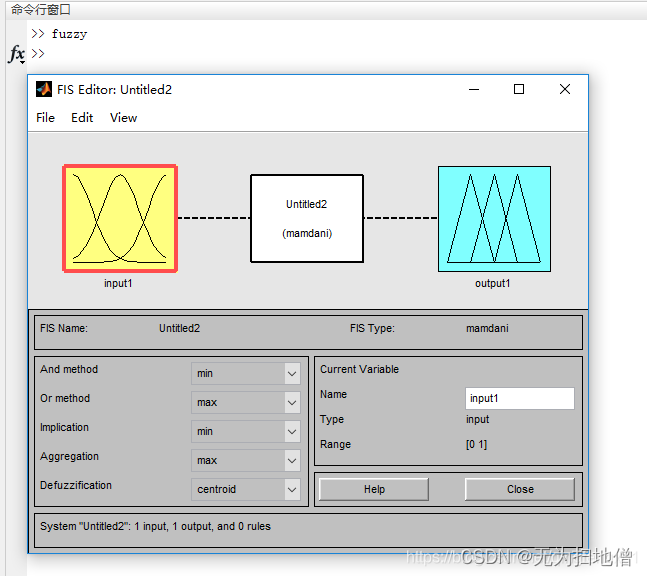
接下来我们都是在这个窗口中进行fuzzy模糊控制器的设计。-
确定fuzzy模糊控制器结构:即根据具体的系统确定输入、输出量。
我们选择标准的二维控制结构,即输入为误差e和误差变化ec,输出量为控制量u。注意这里的变量还都是精确量。相应的模糊量为E,EC和U,我们可以选择增加输入(Edit->Add Variable)来实现双输入单出结构。
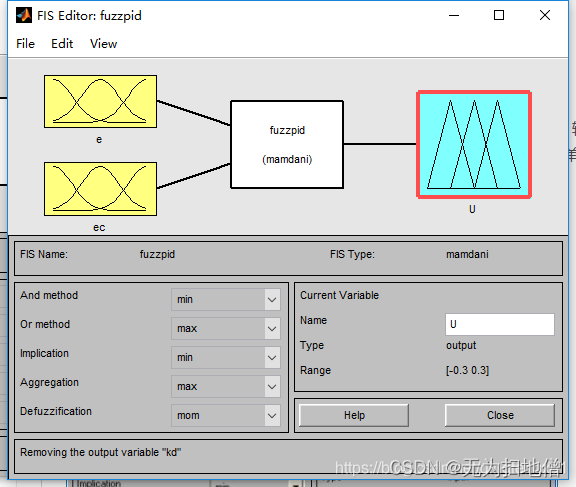
-
输入输出变量的模糊化:即把输入/输出的精确量转化为对应语言的模糊集合。
首先确定描述输入输出变量语言的模糊子集,如{NB,NM,NS,ZO,PS,PM,PB},并设置输入/输出变量的论域,例如我们可以设置误差E(此时为模糊量)、误差变化EC、控制量U的论域均为{-3,-2,-1,0,1,2,3};然后为模糊语言选取相应的隶属度函数。
在模糊控制工具箱中,我们在Edit->MemberShip Function 中即可完成这些步骤。首先打开Edit->MemberShip Function窗口。
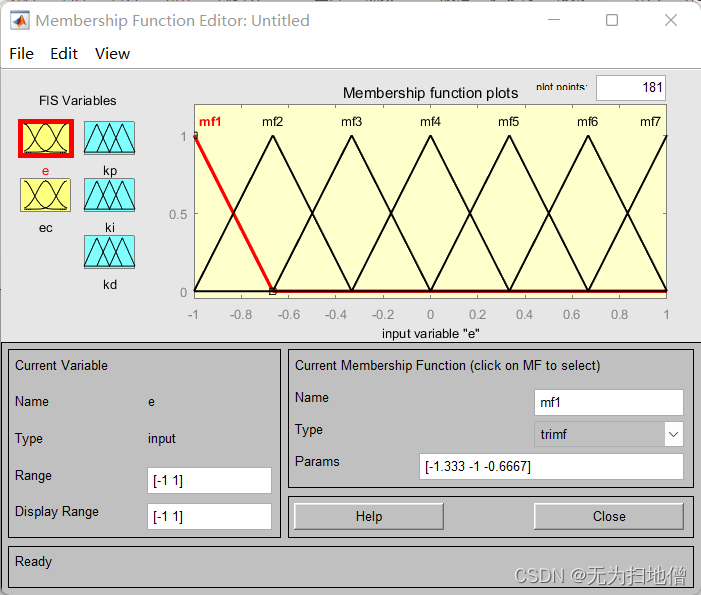
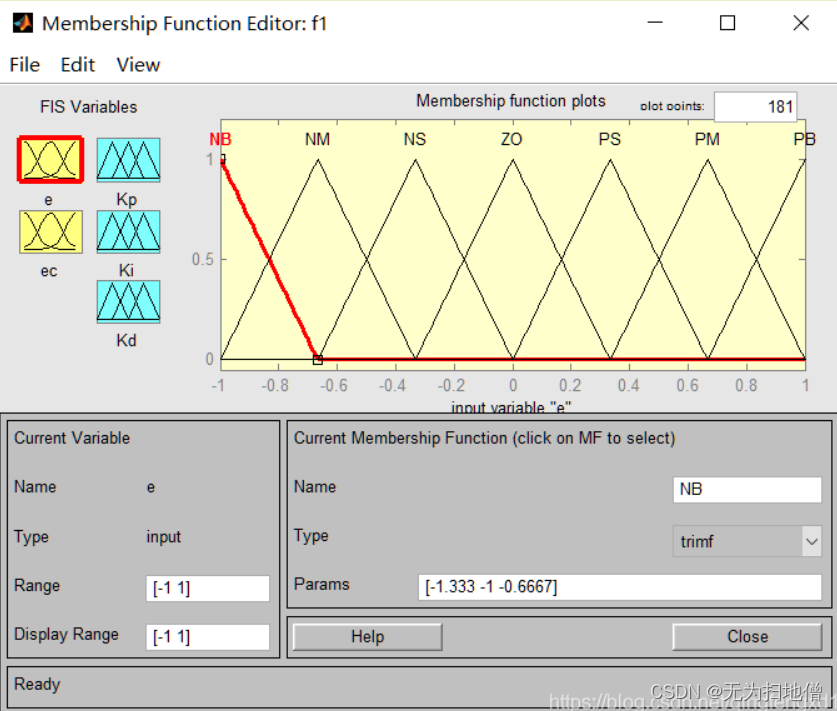
然后分别对输入/输出变量定义论域范围,添加隶属函数(Edit->MFs),以E为例,设置论域范围 为[-1 1],隶属函数的类型为:trimf(三角函数),添加隶属函数的个数为7。
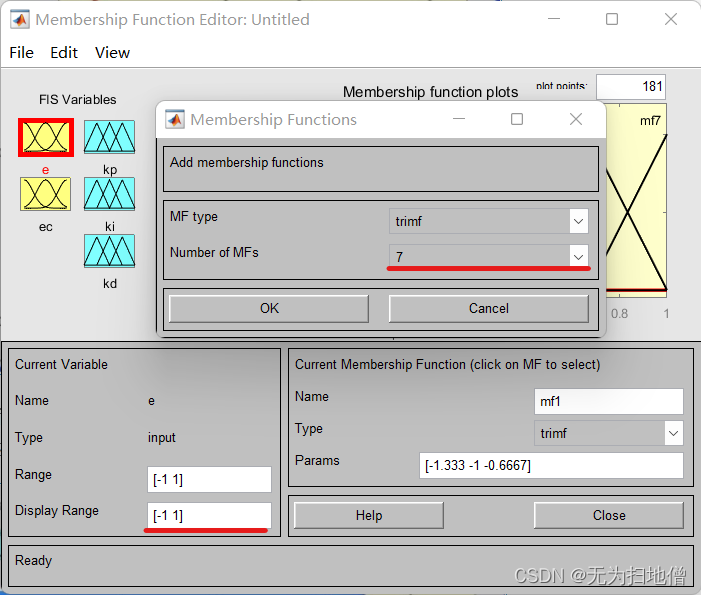
接着根据设计要求分别对这些隶属函数进行修改,包括对应的语言变量,隶属函数类型。
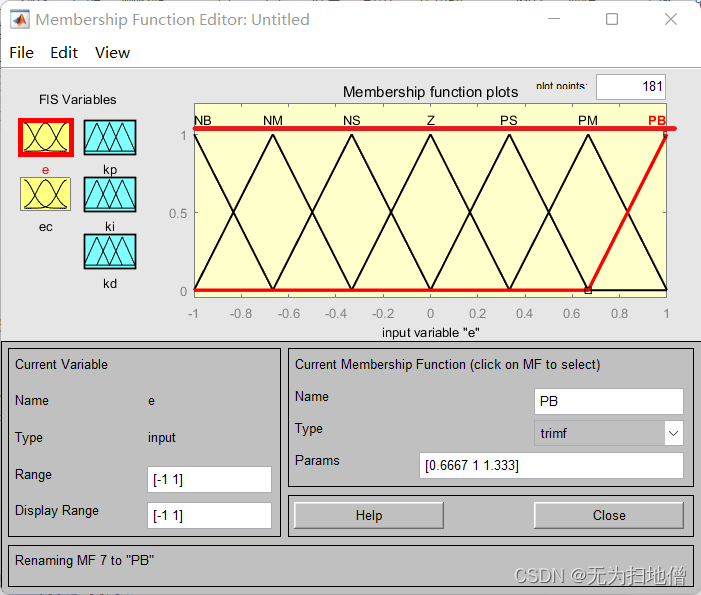
-
模糊推理决策算法设计:根据模糊控制规则进行模糊推理,并决策出模糊输出量。
首先要确定模糊规则,即专家经验。对于我们这个二维控制结构以及相应的输入模糊集,我们可以制定49条模糊控制规则(双击“fuzzy pid”控制器)(一般来说,这些规则都是现成的,很多教科书上都有),如图。
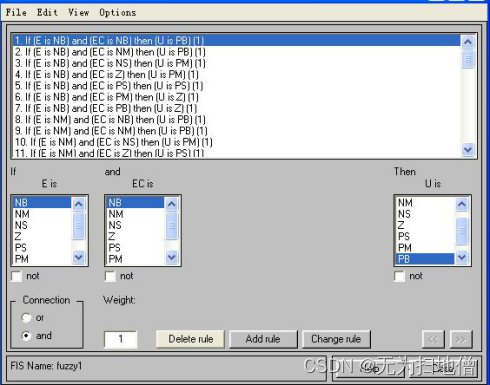
制定完决策之后,会形成一个模糊控制规则矩阵,然后根据模糊输入量按照相对应的模糊推理算法完成计算,并决策模糊输出量。 -
对输出模糊量的解模糊:模糊控制器的输出量是一个模糊集合,通过反模糊化方法判决出一个确切的精确量,凡模糊化方法很多,我们这里选择重心法。
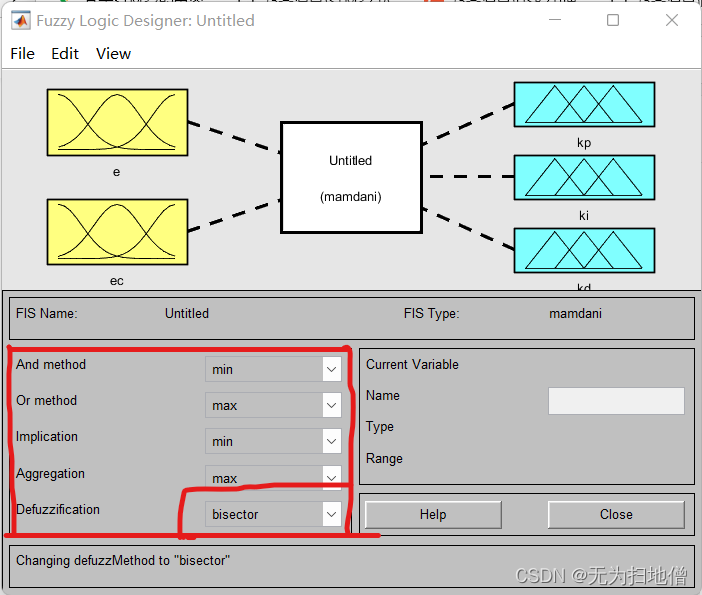
-
然后File->Export->To File,即可得到一个.fis文件,这就是你所设计的模糊控制器。
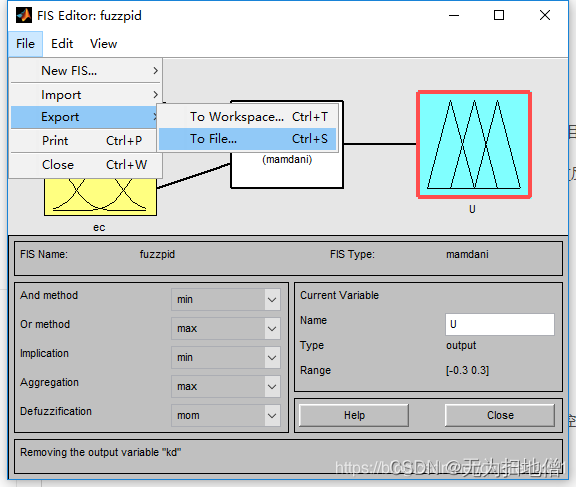
-
simulink中使用fis文件,首先加入fuzzy模块,然后写入模糊文件,注意应用格式加单引号:“fuzzypid.fis”
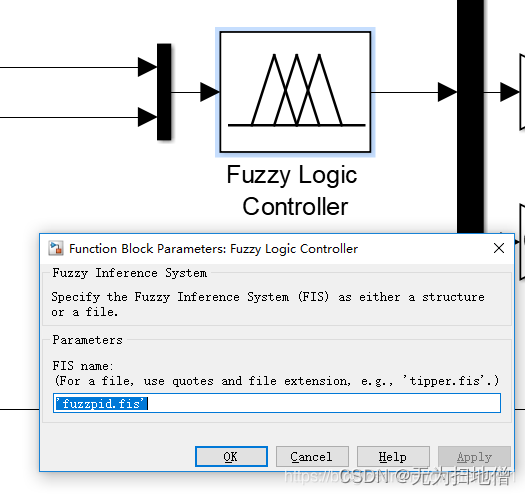
-
研究例子
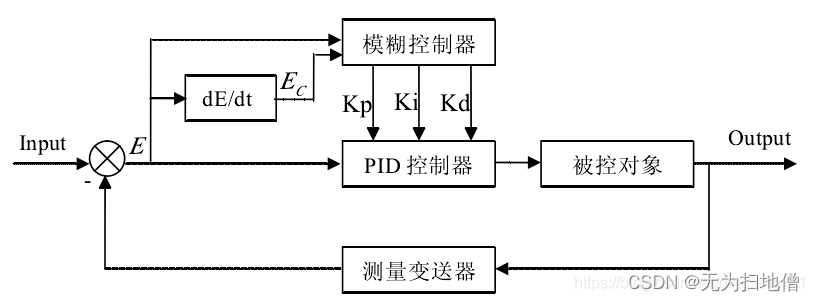
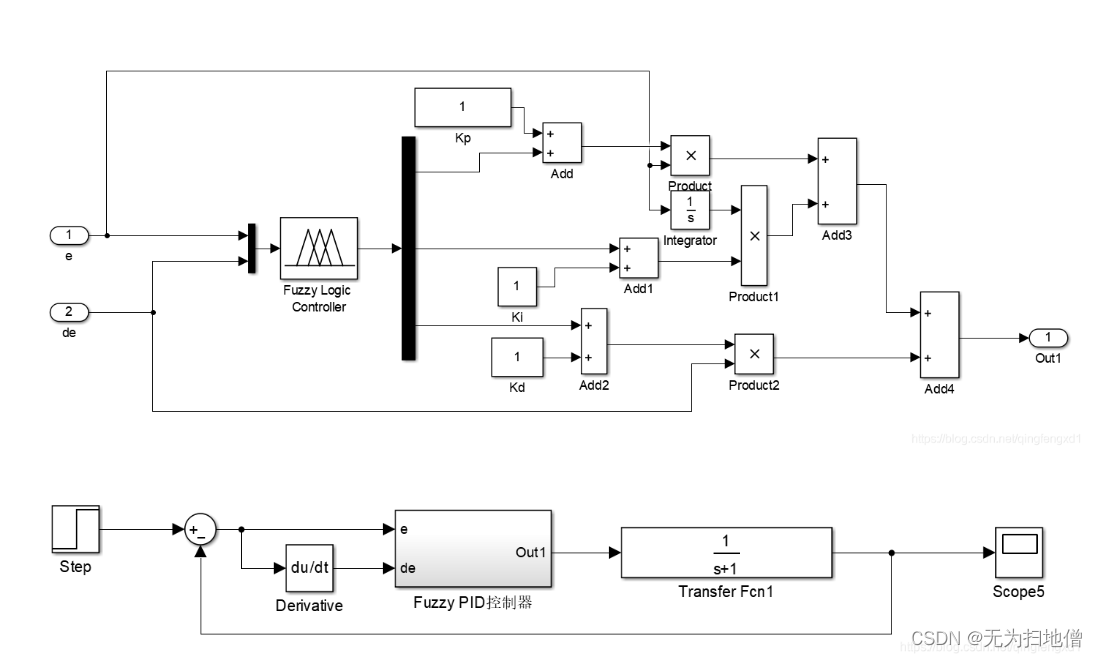
模糊PID控制,即利用模糊逻辑并根据一定的模糊规则对PID的参数进行实时的优化,以克服传统PID参数无法实时调整PID参数的缺点。模糊PID控制包括模糊化,确定模糊规则,解模糊等组成部分。例如小车通过传感器采集赛道信息,确定当前距赛道中线的偏差E及当前偏差和上次偏差的变化EC,根据给定的模糊规则进行模糊推理,最后对模糊参数进行解模糊,输出PID控制参数。
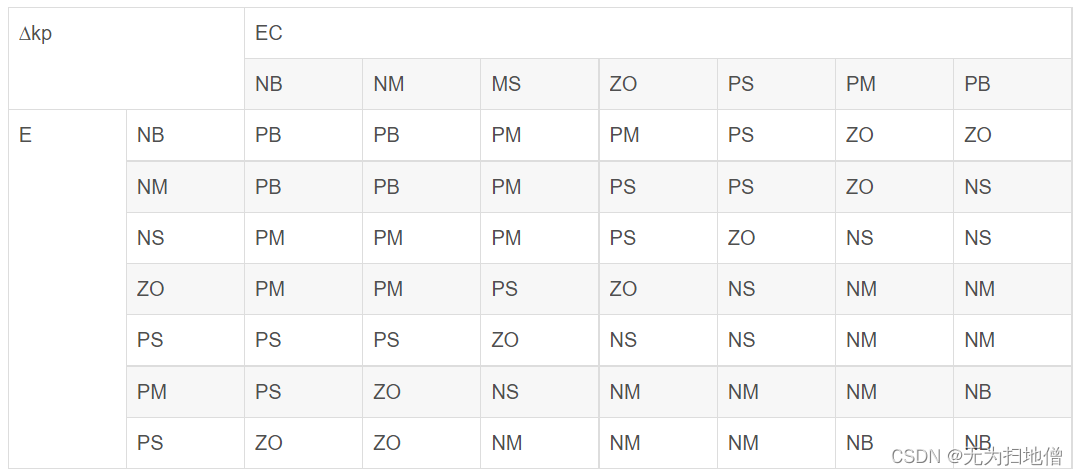
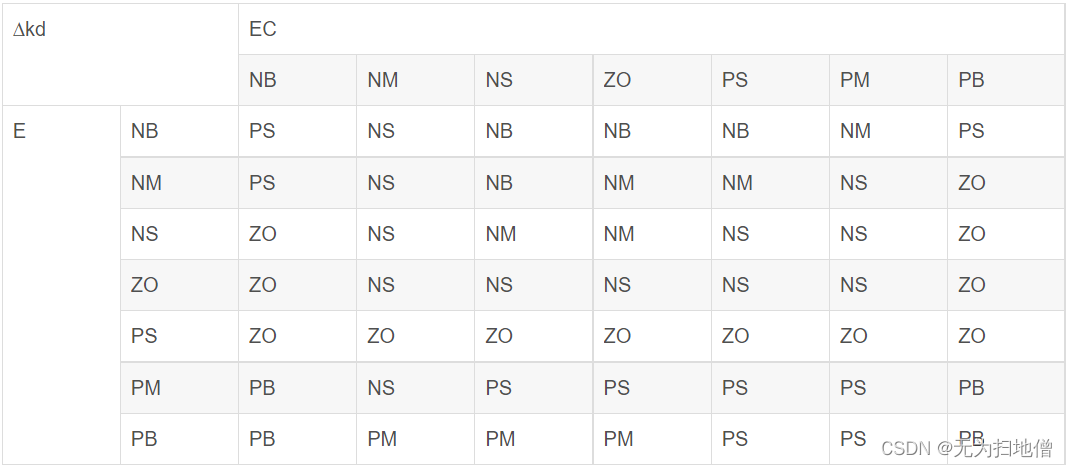
KP的模糊规则控制表
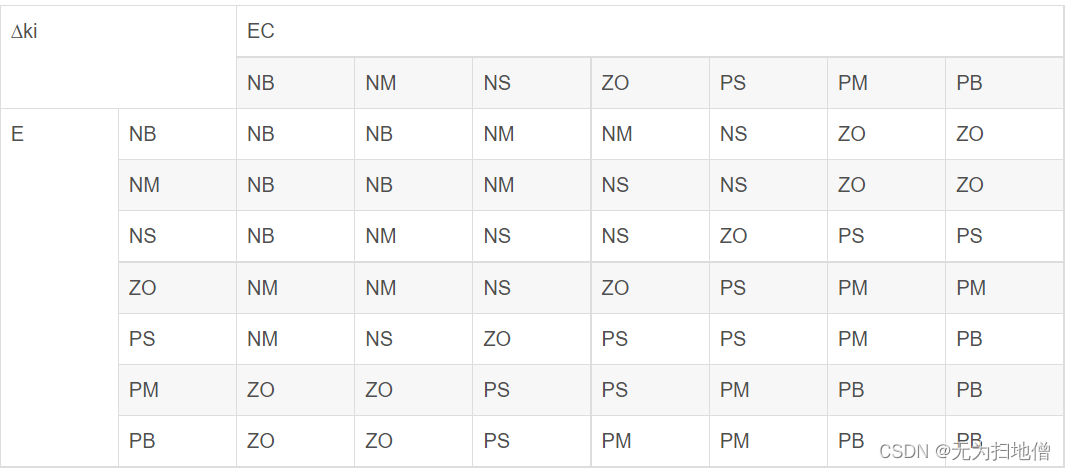
KI的模糊规则控制表
 KD的模糊规则控制表
KD的模糊规则控制表
模糊规则PID推理系统结构图
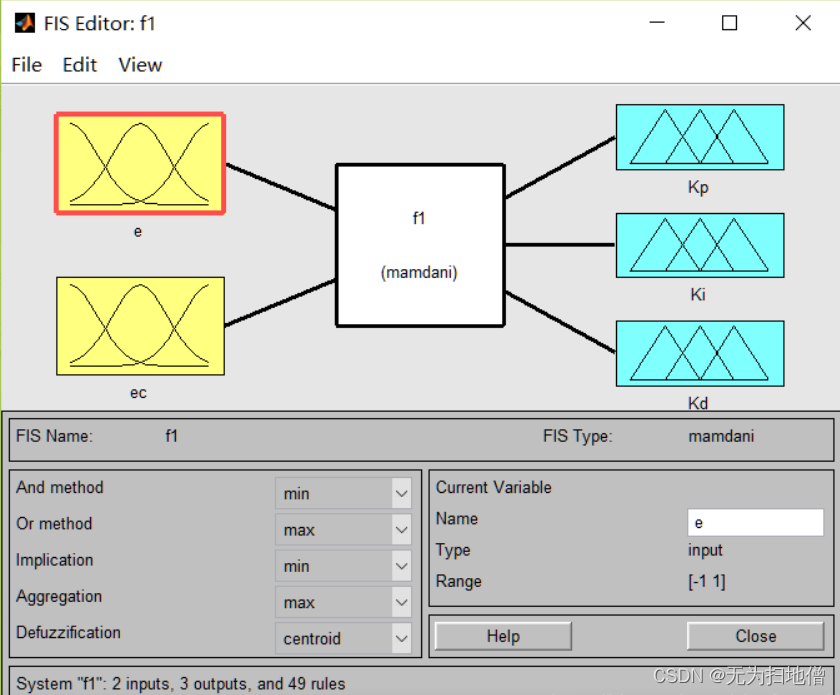
模糊推理系统结构图讲解
- 输入变量的隶属函数三角形函数,误差变量E的隶属函数:
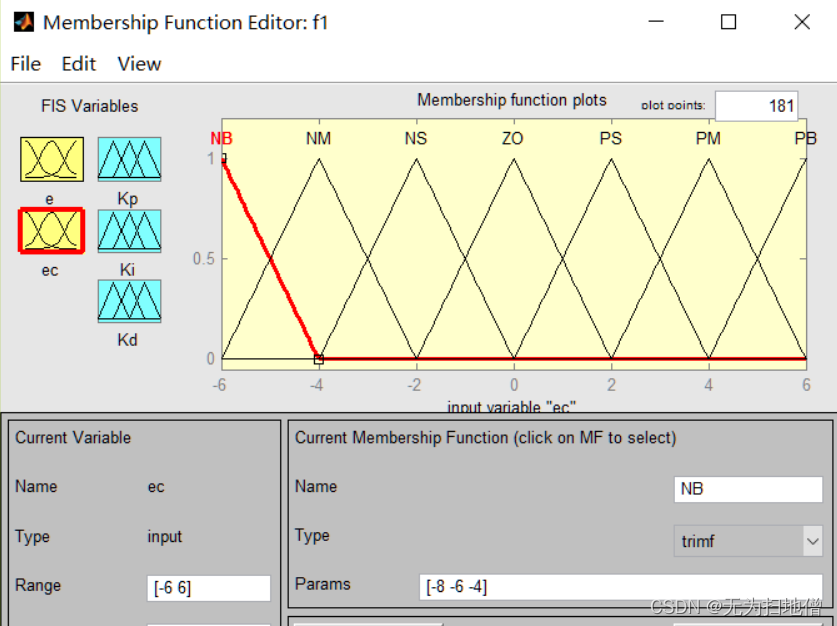
- 误差变化变量EC的隶属函数
输出变量隶属函数
- 输出变量KP的隶属函数
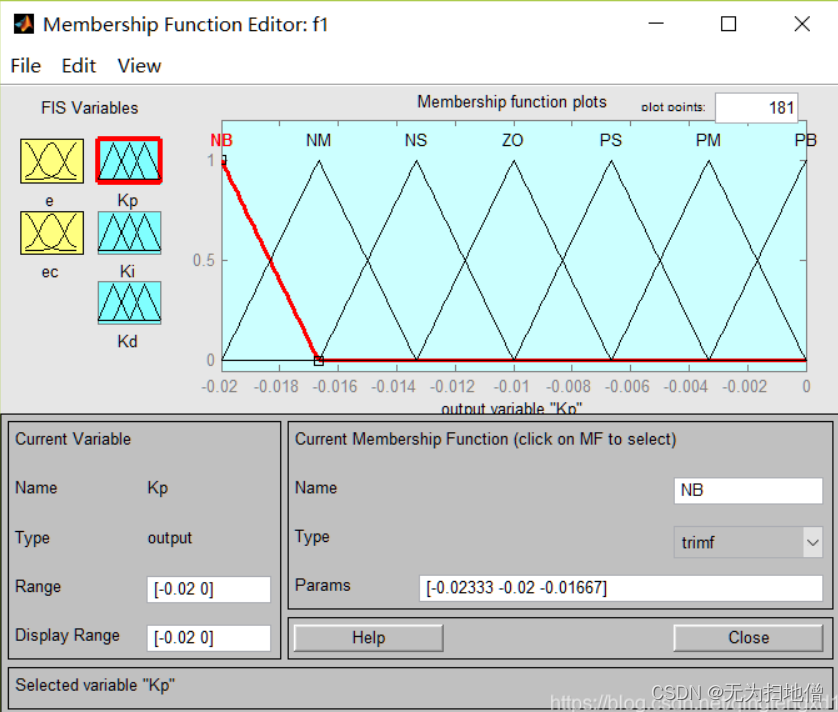
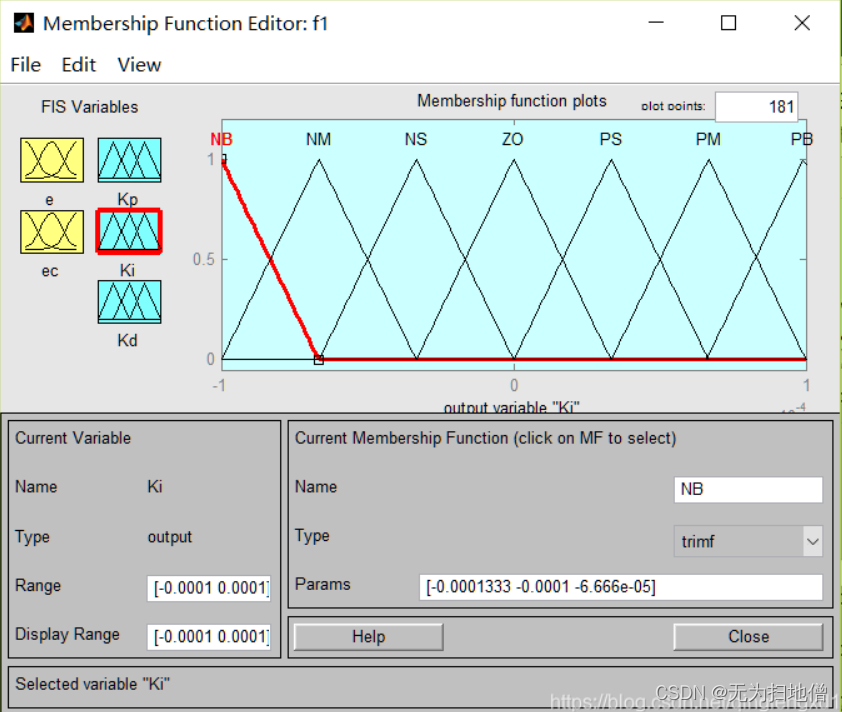
- 输出变量KI的隶属函数
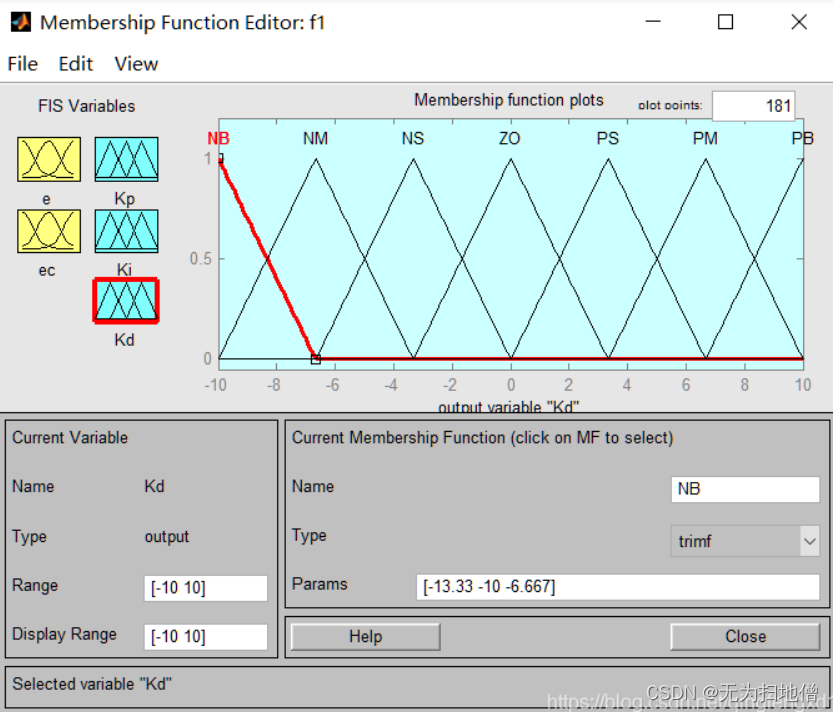
- 输出变量KD的隶属函数
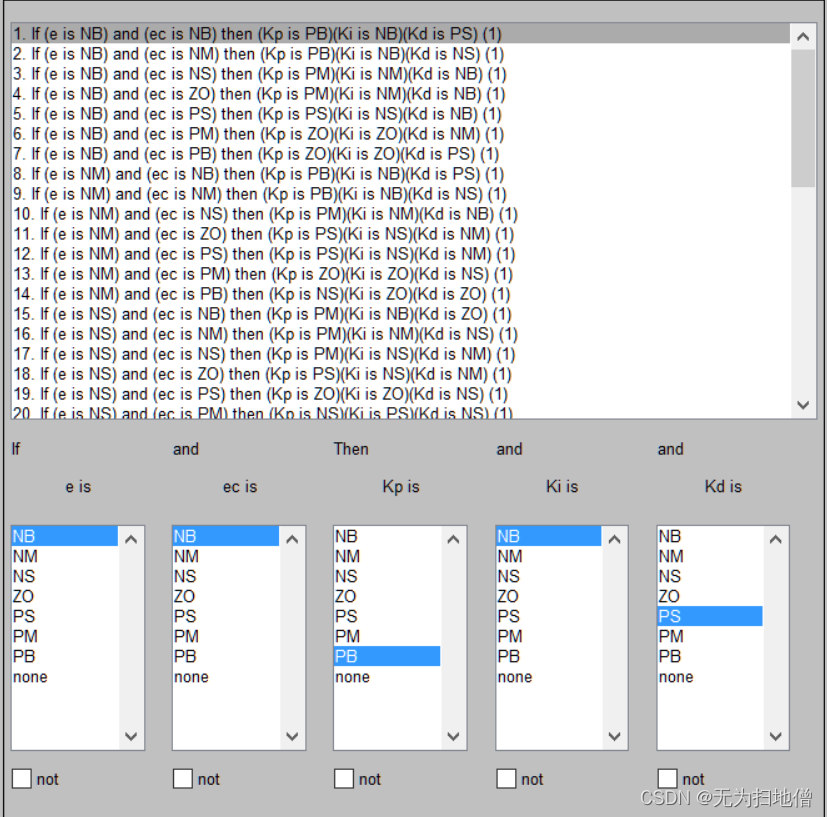
模糊规则编辑器
确定输入/输出隶属函数后,在模糊规则编辑器中,输入表格中的模糊推理规则,共49条,如下图:
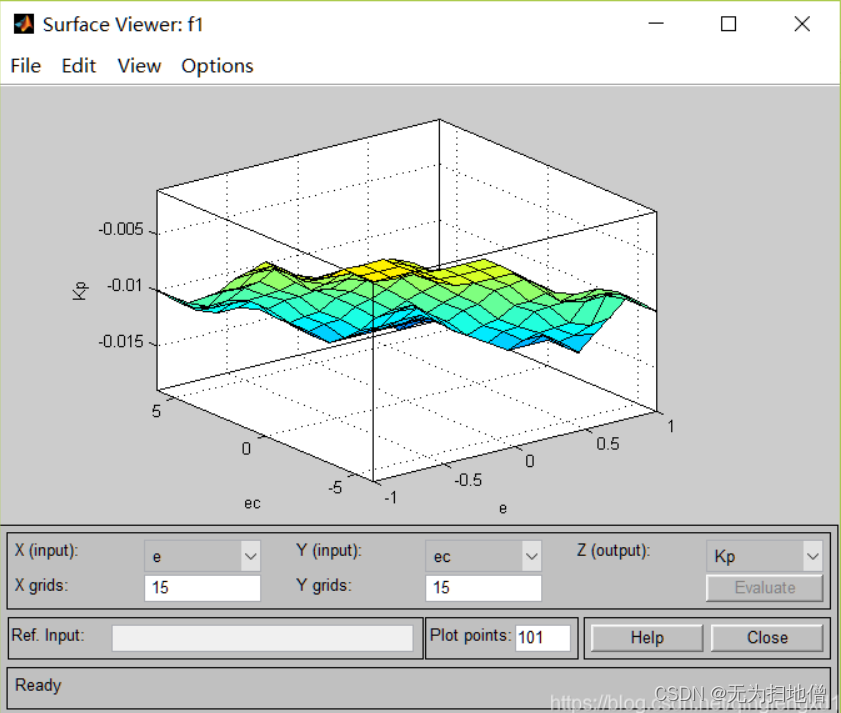
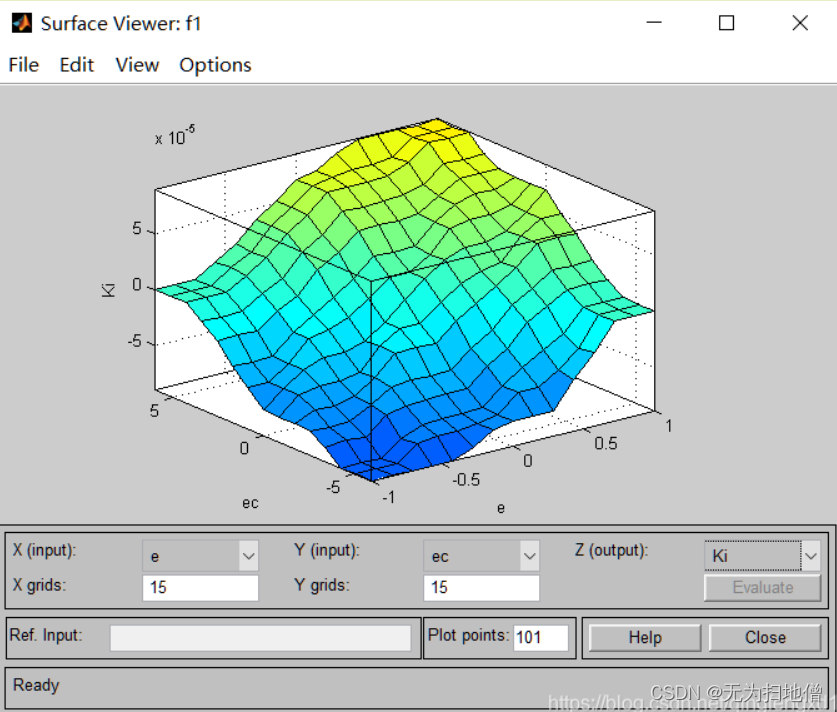
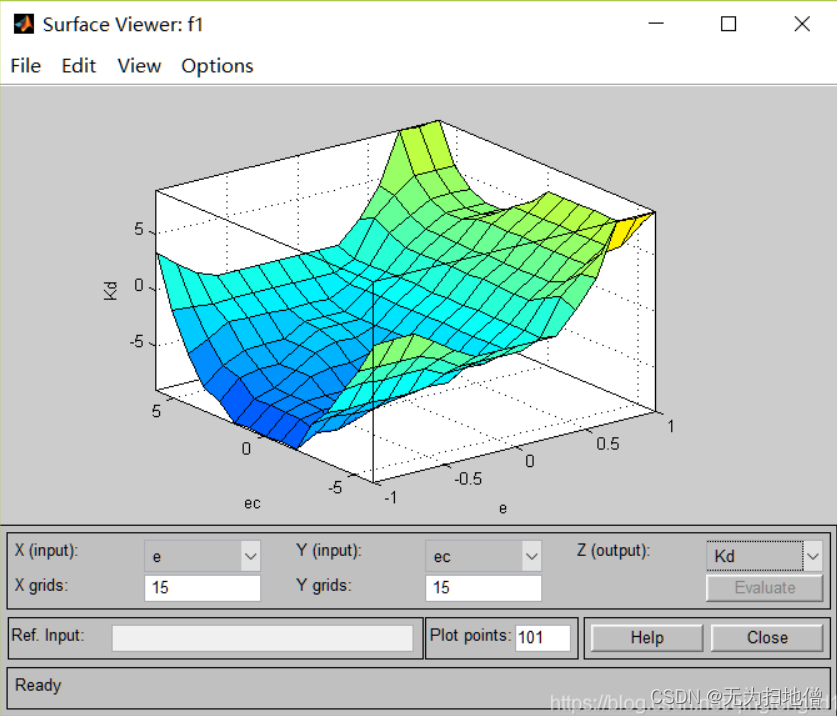
经过模糊规则编辑器编入规则之后,此时得到的三个参数的变化如下图:
- 模糊推理KP变化图
- 模糊推理KI变化图
- 模糊推理KD变化图
最后运行仿真得到结果
研究结果
经过上述一步一步构建仿真结果,最终得到实现通过matlab对模糊PID(Fuzzy)的仿真。
最后
以上就是复杂小猫咪最近收集整理的关于Matlab模拟仿真模糊PID(Fuzzy)的全部内容,更多相关Matlab模拟仿真模糊PID(Fuzzy)内容请搜索靠谱客的其他文章。








发表评论 取消回复