随机抽取(抽奖肯定是随机的对吧),
然后每抽取一个,
每个抽取的数字时间相同
然后每个数字只能抽取一次,也就是抽到一个,后面不会再次被抽到,即6个数字不重复
没抽到一个,LED灯亮一次,
抽完六个之后,停止程序;
通过仿真之后得到:
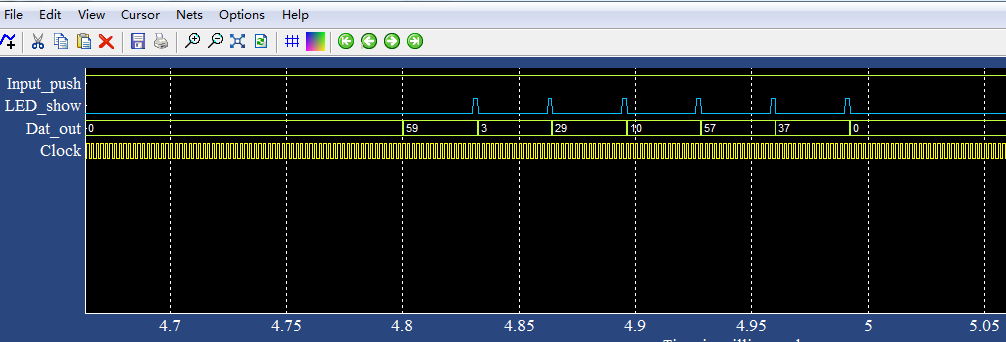
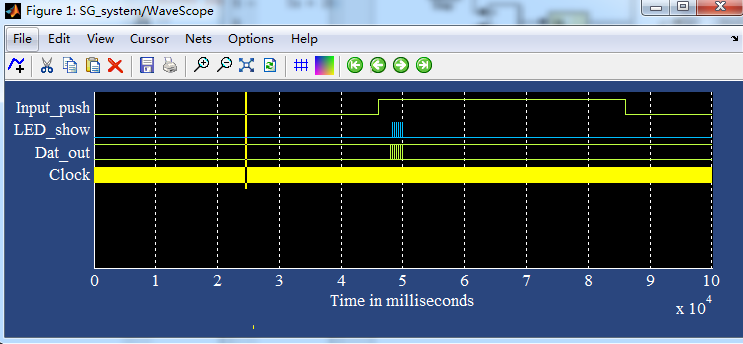
其中LED SHOW表示出现六个随机数,那么LED会亮6次,即6个高电平
然后Dat_out表示输出的六个数字,这里随机数十59 ,3, 29 ,10 ,57 ,37
每次产生的随机数是不同的。
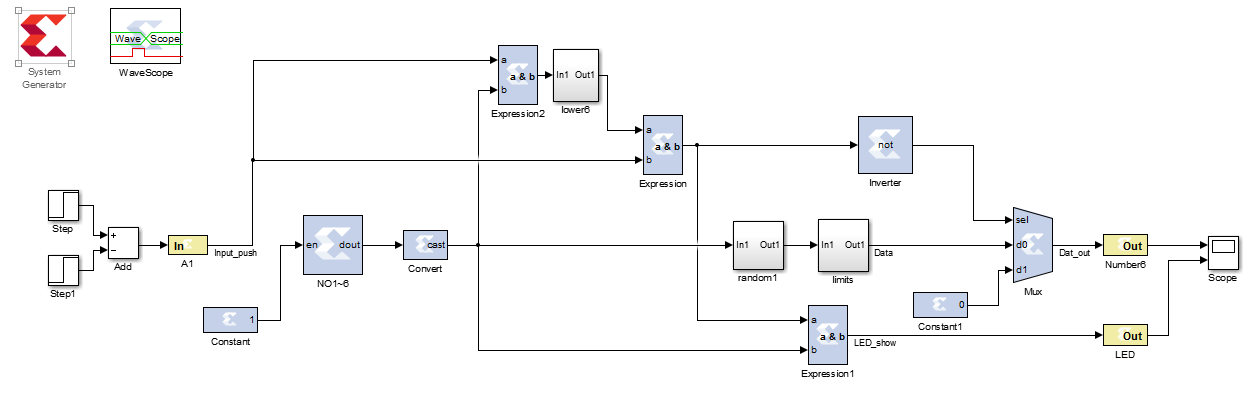
这个SG模型,
运行的时候,现在matlab点击RunMe.m然后再运行SG模型。
关于FPGA中的几个截图:
首先,将SG全部导入到VIVADO,会有如下效果:
顶层VHDL程序截图,程序比较长,有5000多行,因为SG自动转换会产生非常多的程序,这里进行部分截图:
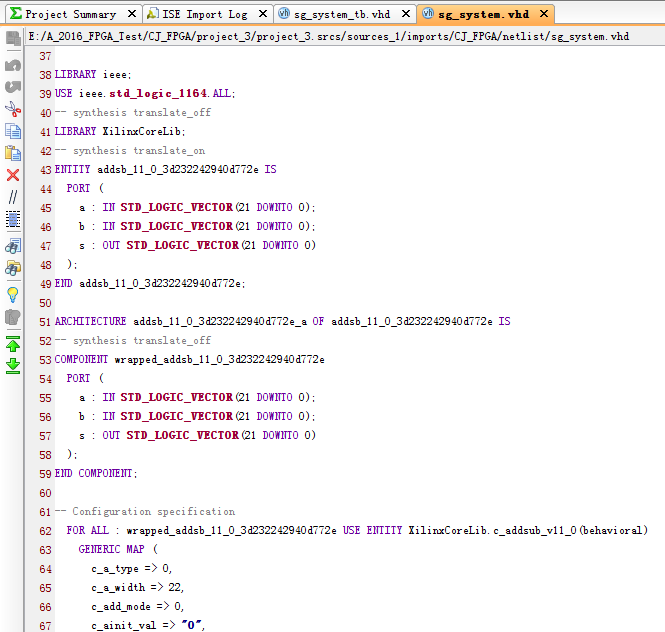
然后这个主程序下面调用了如下几个子文件:
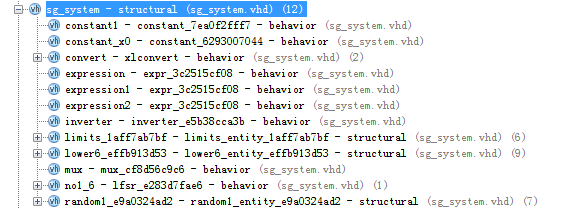
然后测试文件的截图如下所示:
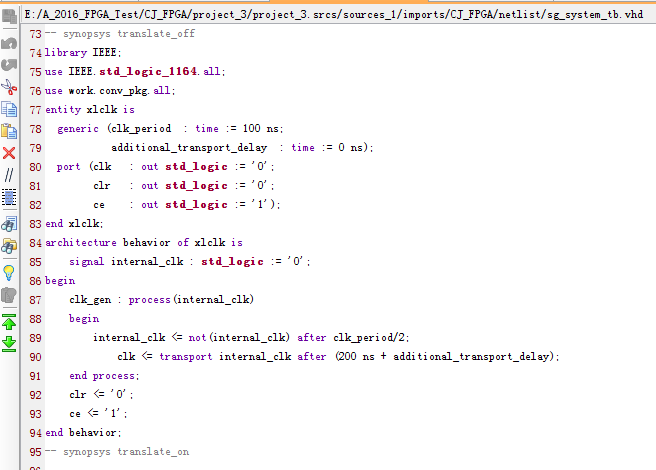
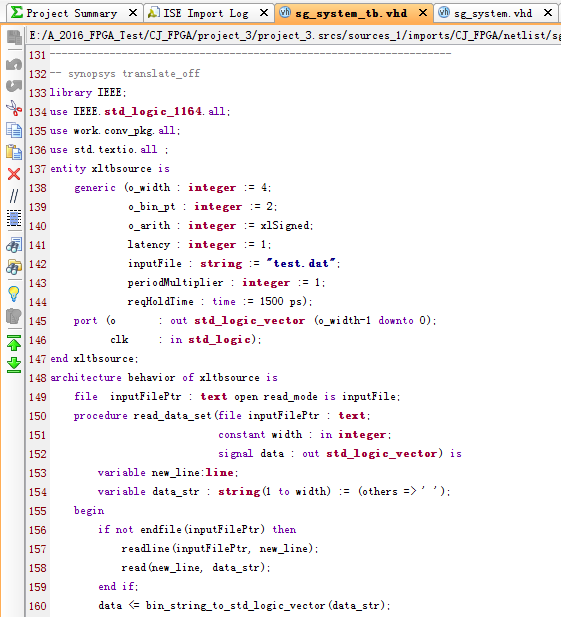
软件版本截图:

vivado:

最后介绍一下SG的设计思路:

这里按区域,单独对每个模块给你介绍一下思路
第一个模块:这个是FPGA的输入信号,也就是上面的input_push信号,模拟实际硬件按钮,当按下的时候,输出高电平,不按的时候输出低电平。
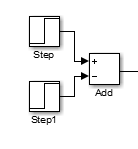
这个模块,为了模拟外部控制输入的功能,通过两个step阶跃信号,组合产生一个高电平信号,其物理含义相当于硬件上按了一下按键,然后驱动设备去产生一个随机数输出指令。
这个的效果就是上图中的input_push
其中其对应的SG输入接口参数如下所示:
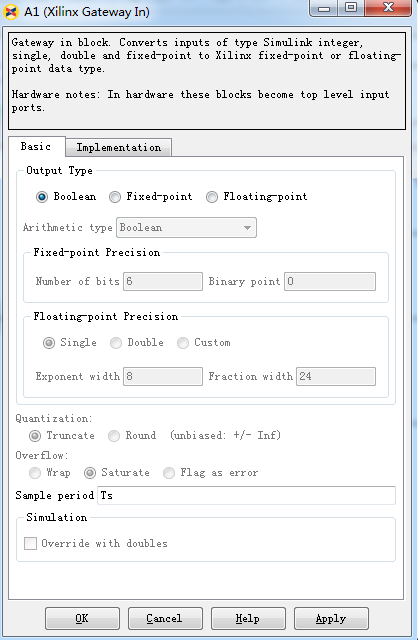
第二个模块:这个是产生使能信号模块,驱动后面的随机数发生器模块。
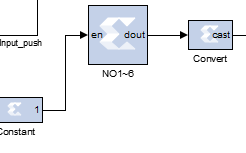
其中,constant模块一直输出高电平,相当于NO1~6这个模块,一直处于工作模块。
即,NO1~6这个模块一直在不间断的产生使能控制着后面的随机数发生器模块。
第三个模块:这个模块是产生6判断信号,即当外部按下的时候,产生6个联系的等间隔的数据的使能信号。
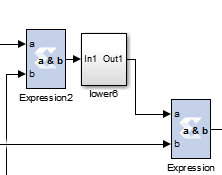
这个模块重点给你介绍一下,其中,lower6的内部结构如下所示:
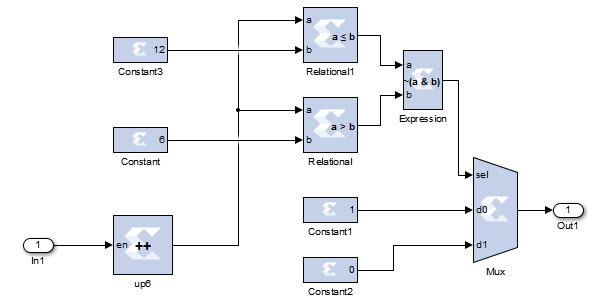
这个模块的含义是,首先通过计数器up6,产生不断增加的计数,1,2,3,4.。。。。。
然后由于我们要产的是6个等间隔的随机数,所以,在这里,我们选择了计数器计数到7到12这6个数的时候产生随机数。这个部分模块为:
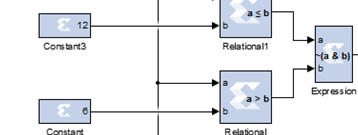
即大于6,小于等于12,也就是上面说的7到12。
当然也可以其他的位置,只要满足6个间隔就可以了,不过这里7到12设置好了,其他各个模块参数都根据7到12设置的,如果要改的话,其他模块也得改,所以这里不建议改这个参数。
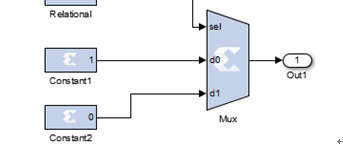
然后这个是使能输出,当计数器计数到7到12这六个数字的时候,mux输出1,否则输出0,
这么建模的功能,就可以保证了后续模块等间隔输出6个数字了。
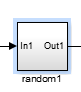
第四个模块:这个模块是核心模块,就是用来产生随机数的模块,这个模块的思路基于FPGA伪随机序列的设计思想,由于伪随机数,根据FPGA内部子带的LSFR单元,通过配置反馈信号以及寄存器输出值,就可以产生伪随机序列。通过设置不同的初始值,使得LSFR以一个较长周期才出现重复数据的情况,从而保证连续的六个数是不同的。
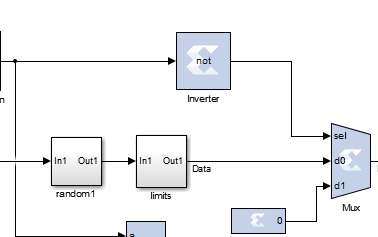
首先说一下这个inverter模块,这个模块就是前面计数器计数6次后的使能,然后取反,即1变0,0变1这样操作,这个是为了配合后一级电路的使能同步起来,才取了反。然后取反再控制里面的MUX。
如果MUX的sel接口输入的是1,那么d0就输出
这个产生的随机数,
如果sel输入的是0,那么d0就输出的是0.
这么处理的目的就是,保证只有6个随机数被输出。而当输出到第六个之后,mux就输出0了,表明完成了6个随机数的输出。
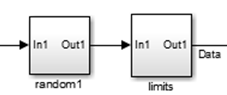
下面重点介绍一下这个随机数产生模块:
这个是产生不重复随机数的模块。
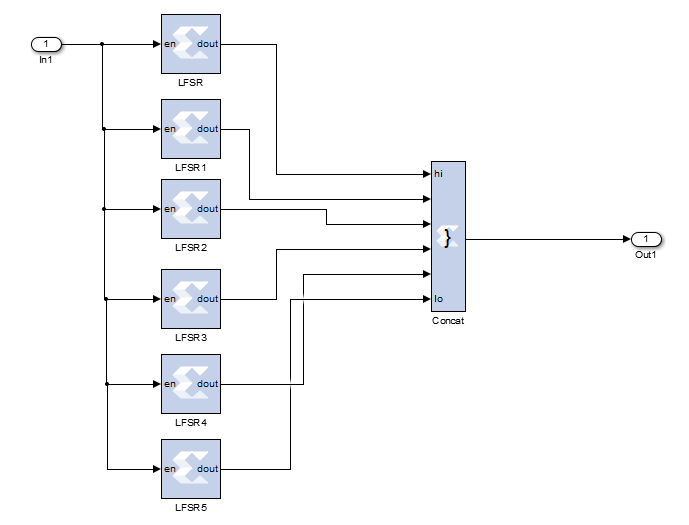
这里的功能,通过FPGA的LSRF模块产生一个6位位宽的随机数,这里简单的介绍一下的LSRF的原理。LSRF即线性反馈移位寄存器
最近一直在研究信道编码,发现在信道编码里面有一个电路比较重要也比较有趣,那就是线性反馈移位寄存器 LFSR ,相信大家对 LFSR 电路也不陌生了,在通信领域lfsr有着很广泛的应用,比如说M序列,扰码,信道编码,密码学这方面都有很广泛的应用,LFRS的结构一般如下图:
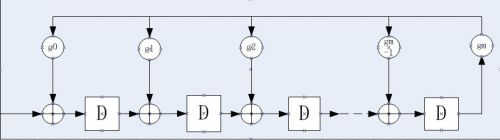
其中他需要一个生成多项式为:
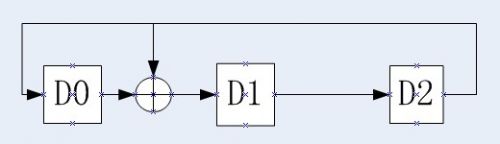
这个多项式是一个本原多项式,然后知道这个电路有一些有意思的性质,下面我以m = 3 来做个例子具体的电路图如下所示:
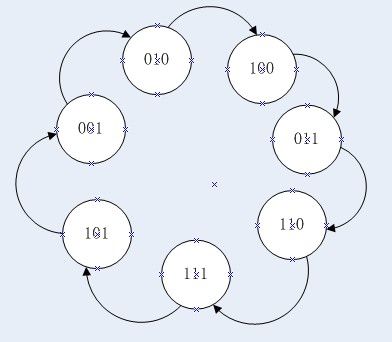
假设开始的时候(D2,D1,D0 ) = (0,0,1),那么每过一个时钟周期会进行跳变一次,
可以看到具体的跳变如下所示: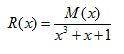
然后我们可以看到这个计数器循环起来了,很好玩吧,无论进入那样一个状态除了0之外,都可以循环着回来,其实这里就相当于了一个3bit的伪随机数,很有意思,不是所有的多项式都有这个特性,我们现在在从数学上面来看看这个问题,其实最上面的电路是可以看成是一个除法电路,在Galois域的一个除法电路。现在假设的是R(x)是寄存器中剩余的数据,M(x)是输入的码字多项式,然后数学公式可以表示成:
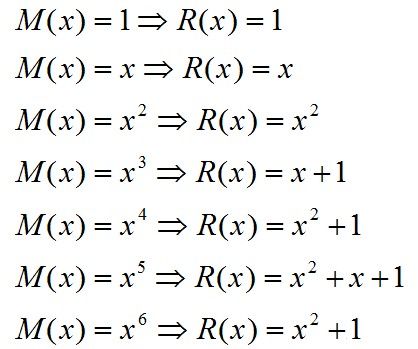
然后我分别计算出了M(x)的各种情况,
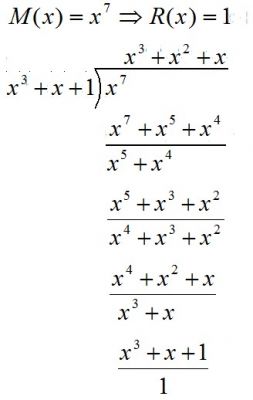
开始仿真,自动跳出仿真器:

仿真结果如下所示:

这个结果和之前的SG中的仿真结果是一样的说明是在正确的:

最后
以上就是彩色吐司最近收集整理的关于基于system generator的LED控制模型设计的全部内容,更多相关基于system内容请搜索靠谱客的其他文章。








发表评论 取消回复