汽车二自由度模型公式推导及simulink模型——传递函数、状态空间

二自由度车辆方程

为便于掌握操纵稳定性的基本特性，我们将一对简化为线性二自由度的汽车模型进行研究，分析中忽略一下几点：
1、忽略转向系统的影响，直接以前轮转角作为输入。
2、忽略悬架的作用，认为汽车车厢只作平行于地面的平面运动，即汽车沿z轴的位移，绕y轴的俯仰角与绕x轴的侧倾角均为零。
另外，汽车沿着x轴的前进速度u视为不变。因此，汽车只有沿y轴的侧向运动与绕z轴的横摆运动这样两个自由度。此外，汽车的侧向加速度限定在0.4g以下，轮胎侧偏特性处于线性范围。在建立运动微分方程时还假设：驱动力不大，不考虑地面切向力对轮胎侧偏特性的影响，没有空气动力的作用，忽略左、右车车轮轮胎由于载荷的变化而引起轮胎特性的变化以及轮胎回正力矩的作用。这样，实际汽车便简化成为一个两轮摩托车模型。

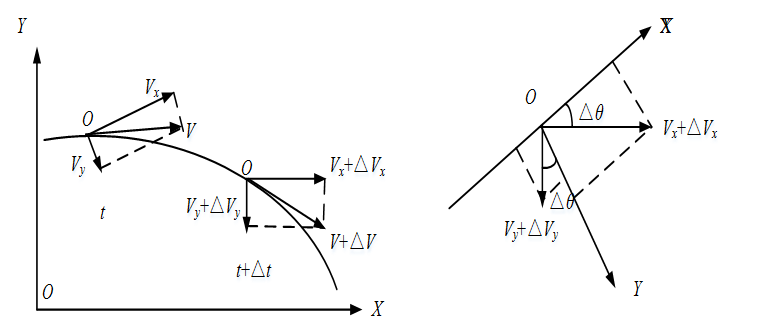
首先确定汽车质心的（绝对）加速度在车辆坐标系上的分量，如上图所示：
OX与OY为车辆坐标系的纵轴与横轴。质心速度V于t时刻在OX轴上的分量为Vx，在OY轴上的分量为Vy。由于汽车转向行驶时伴有平移和转动，在t+△t时刻，车辆坐标系中质心速度的大小与方向均发生变化，而车辆坐标系的纵轴与横轴的方向亦发生变化。考虑纵向速度Vx和侧向速度Vy随OX和OY所发生的随机(t+t)变化，我们假设幅度小，则：
随OX的变化
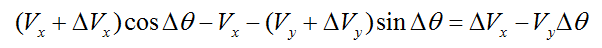随OY的变化
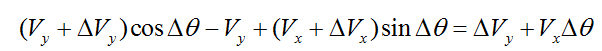定义随OX的变率为ax (纵向加速度)，随OY的变率为ay (侧加速度)

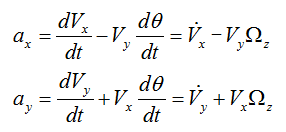
简易汽车横摆动力学模型：

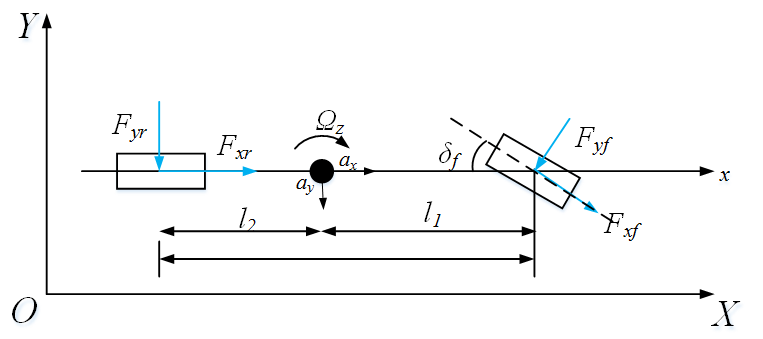
图中，δf为前轮转角，Fxf，Fyf分别是前轮的纵向力和侧向力。Fxr，Fyr分别是h后轮的纵向力和侧向力。ax和ay分别为车辆质心在纵向和侧向的加速度。l1为质心到前轴的距离，l2为质心到后轴的距离。Ωz为车辆横摆角速度。规定顺时针为正方向。车辆动力学方程如下：

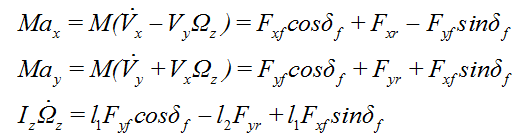
考虑的轮胎的侧偏特性。则有如下公式：

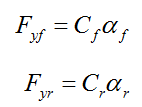
汽车横摆瞬时运动关系如下图

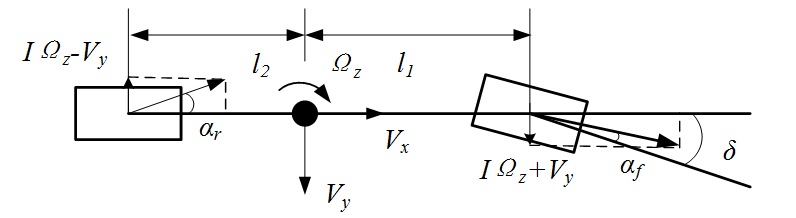
根据上图关系可知：

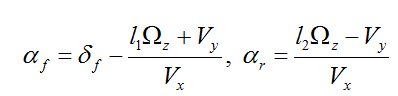
带入车辆动力学方程整理得：

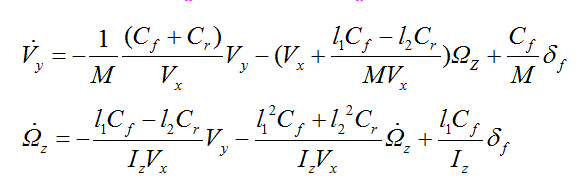
上述是非常重要的两个公式，衡量了瞬态汽车运动时的侧向加速度和横摆角速度。为简化表达式。我们设如下参数：


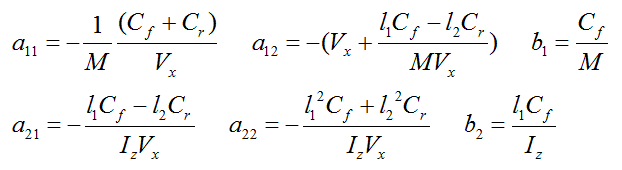
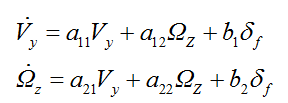
上述方程可以通过传递函数和状态空间表示。这两种方法皆能用来设计闭环控制系统，通过将所测得的汽车性能参数调整至理想数值来提升车辆稳定性，也及ESC系统作用

传递函数法

上述等式可写为：


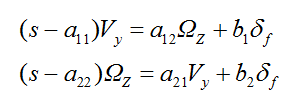
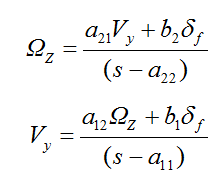
联立可得：

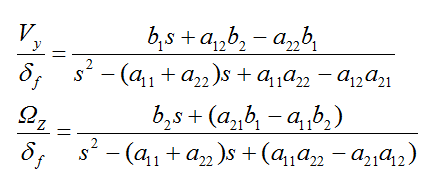
对照二阶系统标准的传递函数形式则上式可写为：


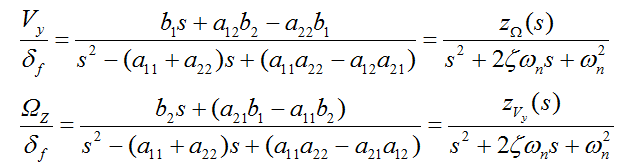
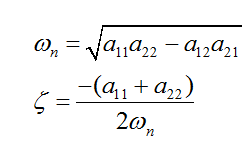
上式转化为传递函数的标准形式：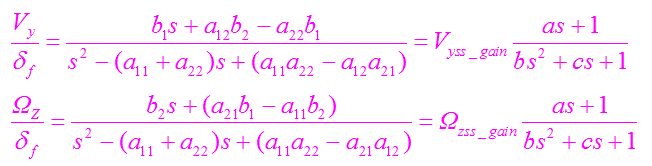
(过程推导)


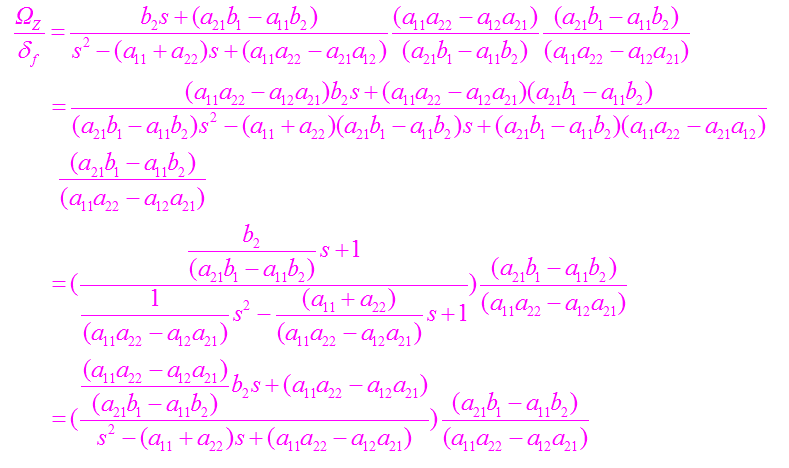
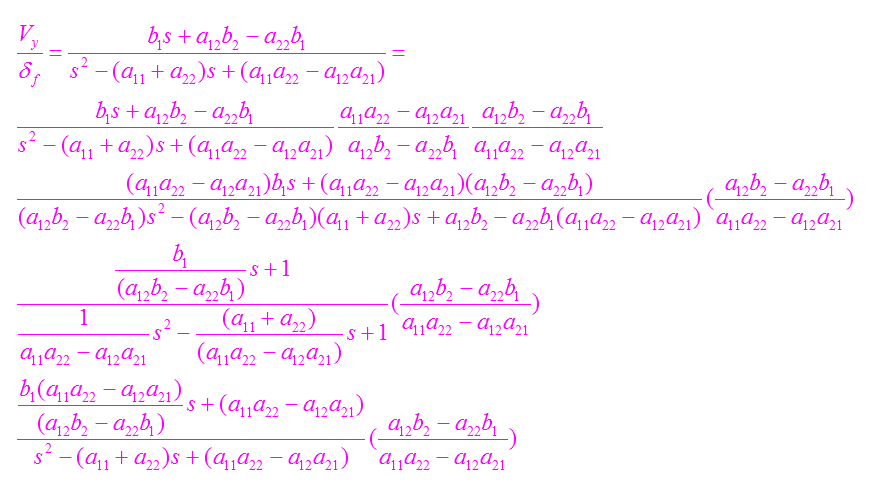
角速度稳态增益和速度增益如下：

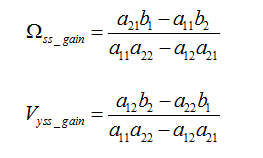
状态空间

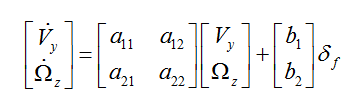
基于上述公式推导，简易版车辆二自由度simulink模型如下

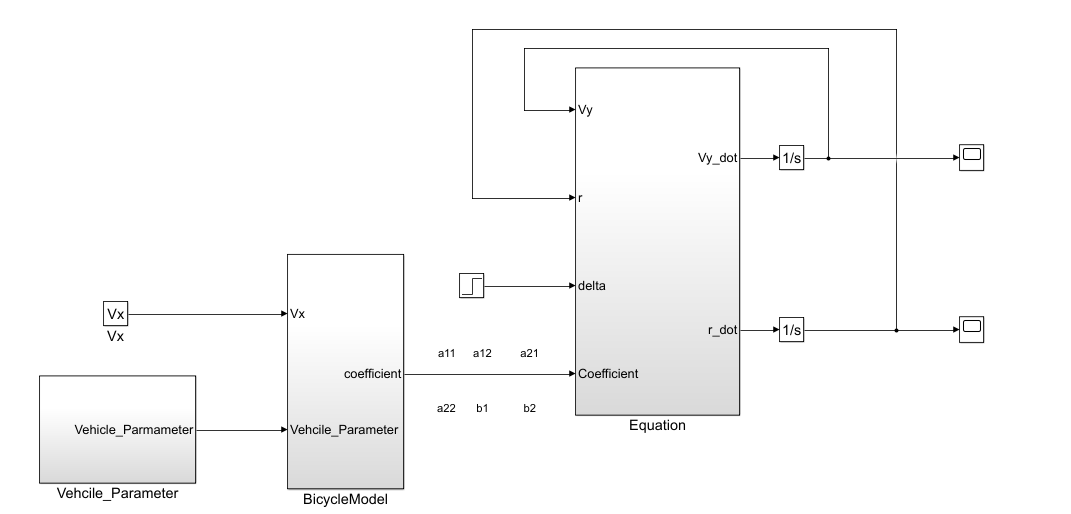
最后

以上就是鲜艳美女为你收集整理的汽车二自由度模型公式推导及simulink模型——传递函数、状态空间的全部内容，希望文章能够帮你解决汽车二自由度模型公式推导及simulink模型——传递函数、状态空间所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。