数字调制解调—MSK
- 1 MSK时域特征
- 2 MSK产生方法
- 3 MSK调制仿真
- 4 MSK解调仿真
1 MSK时域特征
二进制最小频移键控(Minimum Shift Keying , MSK)信号的表示式可写为:
式中,wc是载波频率,T是码元宽度,ak是第k个码元的数据(取值为±1),φk是第k个码元中的相位常数,他在kT≤t≤(k+1)T中保持不变。
当ak从+1变化到-1,传信频率从f1变化到f2,角频率Δw= π T frac{π}{T} Tπ,由w=2πf,则Δf= 1 2 T frac{1}{2T} 2T1,调制指数h=Δf·T=0.5.
MSK其实就是一种FSK,只是传信频率f1和f2在一个码元周期内严格保证相位差180°,这是因为Δθ=Δw·T=2πΔf·T。
根据SMSK(t)的表达式,将其拆开可得:
上式即为MSK的正交表示形式,设I支路和Q支路分别为xI(t)和xQ(t)。
令I=cosφk,Q=akcosφk,显然I、Q、ak之间存在某种转化关系,通常以差分编码的形式对ak进行处理,奇数元素给I支路,偶数元素给Q支路,这样上下支路便错开了一个码元周期T,满足传信频率要求的相位差。
2 MSK产生方法
- 对输入数据序列进行差分编码。
- 把差分编码器输出数据用串并转换器分成两路,并且相互交错一个码元宽度T。
- 用加权函数cos( π t 2 T frac{πt}{2T} 2Tπt)和sin( π t 2 T frac{πt}{2T} 2Tπt)分别对两路数据进行加权。
- 用两路加权后的数据分别对正交载波coswct和sinwct进行调制
- 将两路输出信号进行叠加
3 MSK调制仿真
ps=1*10^6; %码速率为1MHz
Fs=16*10^6; %采样速率为16MHz
fc=3*10^6; %载波频率为3MHz
N=100; %数据码元个数
Len=N*Fs/ps; %仿真数据的长度
x = randint(N,1,2)'; % 产生随机数据做为数据码元
%x=ones(1,N);
dx=ones(1,N);
for i=1:N
if x(i)==0
x(i)=-1;
end
end
%求原码的相对码dx
for i=2:N
if x(i)==1
dx(i)=-dx(i-1);
else
dx(i)=dx(i-1);
end
end
%将相对码按奇偶序号分成两路数据,形成IkQk
di=ones(1,N);
dq=ones(1,N);
%取dx的偶数位,并列两位为di
for i=2:2:N
di(i:i+1)=dx(i);
end
%取dx的奇数位,并列两位为dq
for i=1:2:N-1
dq(i:i+1)=dx(i);
end
%对原始BIT数据进行Fs/ps倍重采样
udi=ones(1,N*Fs/ps);
udq=ones(1,N*Fs/ps);
for i=1:N
udi(Fs/ps*(i-1)+1:Fs/ps*i)=di(i);
udq(Fs/ps*(i-1)+1:Fs/ps*i)=dq(i);
end
%产生MSK信号所需的载波信号
t=0:1/Fs:(Len-1)/Fs;
cf0c=cos(2*pi*fc.*t);
sf0c=sin(2*pi*fc.*t);
cfps=cos(pi*ps/2.*t);
sfps=sin(pi*ps/2.*t);
%正交调制法产生msk信号
msk=udi.*cfps.*cf0c-udq.*sfps.*sf0c;
%绘制MSK信号的频谱及时域波形
figure(2);
%求MSK信号的FFT变换
m_msk=20*log10(abs(fft(msk,2048)));
m_msk=m_msk-max(m_msk);
%设置幅频响应的横坐标单位为MHz
x_f=1:length(m_msk);
x_f=x_f*Fs/length(m_msk)/10^6;
%绘制MSK信号的频谱
subplot(211);
plot(x_f,m_msk);axis([0 Fs/2/10^6 -80 0]);
legend('MSK信号频谱');
xlabel('频率(MHz)');ylabel('幅度(dB)');grid on;
%绘制MSK信号的时域波形
subplot(212);
%设置横坐标单位为us
LT=100;
x_t=0:1/Fs:(LT-1)/Fs;
x_t=x_t*10^6;
plot(x_t,msk(100:100+LT-1))
legend('MSK信号时域波形');
xlabel('时间(us)');ylabel('幅度(V)');
仿真结果如图所示:
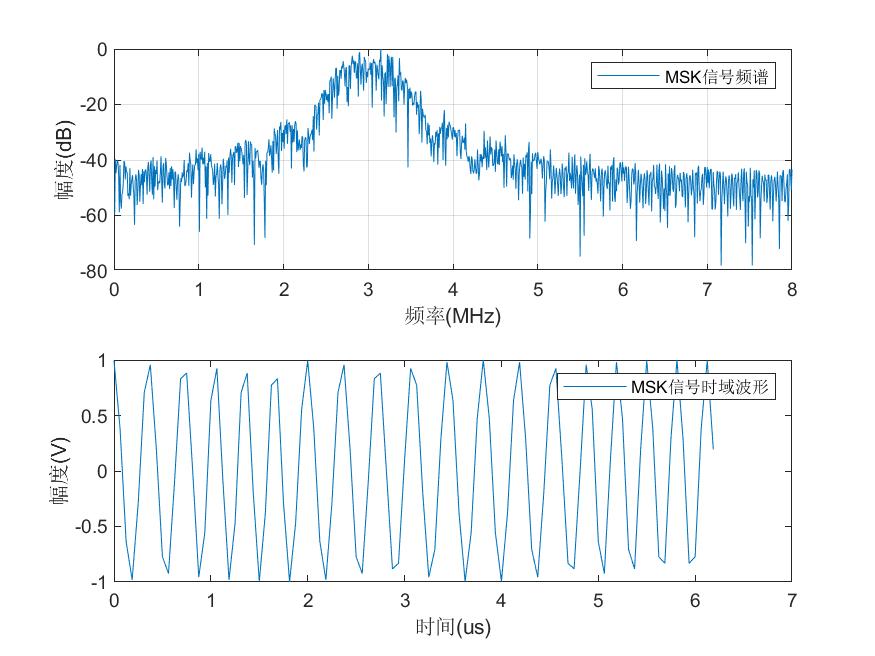
可以看出,0dB点大约在3MHz处,正是载波频率。
4 MSK解调仿真
本文采用平方环载波提取的MSK相干解调。已知MSK调制指数h=0.5,经过平方后,即频域相加,角频偏为0.5+0.5=1,故调制指数h=1。另一方面,MSK也属于CPFSK,而调制指数为1的CPFSK功率谱中存在离散分量,分别为二倍传号频率fH和fL。因此,可以用两个锁相环电路分别提取处这两个频率。根据MSK信号特征,可以得到载波fc和时钟fR与两个离散频率分量之间的关系为:
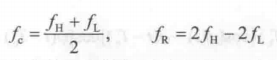
在电路中将两个锁相环锁定的2fH和2fL两个信号相乘,可得到差频分量,然后用低通滤波提取出来,就可得到时钟频率fR信号,它经脉冲形成后得到所需的时钟脉冲,再由此产生各种定时信号。
将二分频后的fH和fL相乘,并经过低通滤波可获得fR/2,其速率与正交两路的速率相同,可用于正交两路数据的判决,信号如下:
S
S
S1
(
t
)
=
c
o
s
(
2
π
f
(t)=cos(2πf
(t)=cos(2πfH
t
)
=
c
o
s
(
2
π
f
t)=cos(2πf
t)=cos(2πfc
t
+
π
t
/
2
T
)
t+πt/2T)
t+πt/2T)
S
S
S2
(
t
)
=
c
o
s
(
2
π
f
(t)=cos(2πf
(t)=cos(2πfL
t
)
=
c
o
s
(
2
π
f
t)=cos(2πf
t)=cos(2πfc
t
−
π
t
/
2
T
)
t-πt/2T)
t−πt/2T)
具体代码如下
%MSK 解调
%第一种相干解调,需要同时获取fc,fb的载波频率
% demod_i=msk.*cf0c.*cfps;
% demod_q=msk.*sf0c.*sfps;
%平方环相干解调,只需获取fL、fH的载波频率
fL=cos(2*pi*fc.*t-2*pi*ps/4.*t);
fH=cos(2*pi*fc.*t+2*pi*ps/4.*t);
demod_i=msk.*(fH+fL);
demod_q=msk.*(fH-fL);
%低通滤波后,获取I、Q支路基带波形
b=fir1(30,0.5*ps*2/Fs);%设计低通滤波器
f_i=filter(b,1,demod_i);
f_q=filter(b,1,demod_q);
fb=fL.*fH;
rb=filter(b,1,fb);
%绘制解后的I、Q支路基带波形及时钟信号波形
figure(1);
num=800;
x_t=0:1/Fs:(num-1)/Fs;
x_t=x_t*10^6;
subplot(411);plot(x_t,udi(1:num));axis([0 25 -1.2 1.2]);
legend('I支路原始数据时域波形');
xlabel('时间(us)');ylabel('幅度(V)');
subplot(412);plot(x_t,f_i(1:num),'-',x_t,rb(1:num),'--');
legend('I支路解调数据','时钟信号');
xlabel('时间(us)');ylabel('幅度(V)');
subplot(413);plot(x_t,udq(1:num));axis([0 25 -1.2 1.2]);
legend('Q支路原始数据时域波形');
xlabel('时间(us)');ylabel('幅度(V)');
subplot(414);plot(x_t,f_q(1:num),'-',x_t,rb(1:num),'--');
legend('Q支路解调数据','时钟信号');
xlabel('时间(us)');ylabel('幅度(V)');
仿真结果如图所示:
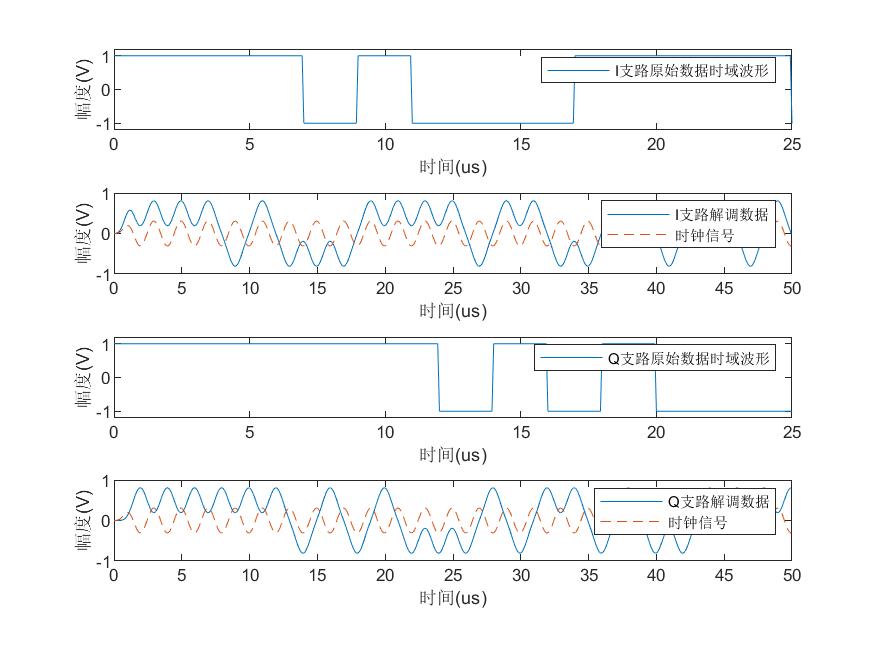
从图中可以看出,对于I支路而言,1/2倍码速率时钟信号与解调后的I支路完全同步,最佳判决时刻为时钟波峰处;对于Q支路而言,1/2倍码速率时钟信号与解调后的Q支路数据完全正交,最佳判决时刻在时钟波谷处。
最后
以上就是平淡小丸子最近收集整理的关于数字调制解调—MSK1 MSK时域特征2 MSK产生方法3 MSK调制仿真4 MSK解调仿真的全部内容,更多相关数字调制解调—MSK1内容请搜索靠谱客的其他文章。








发表评论 取消回复