自动驾驶算法详解(4): 横向LQR、纵向PID控制进行轨迹跟踪以及python实现

69 阅读 0 评论 46 点赞

我是靠谱客的博主孤独钻石，最近开发中收集的这篇文章主要介绍自动驾驶算法详解(4): 横向LQR、纵向PID控制进行轨迹跟踪以及python实现，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

前言：

在量产ADAS或者自动驾驶算法中，横纵向控制往往都是分开控制的，上一篇文章中介绍了如何使用LQR同时进行横纵向的控制，本文将介绍一种横纵向分开控制的思路，将使用LQR算法进行横向控制，同时使用PID算法进行纵向控制。这种方法在很多自动驾驶科技公司比较常见，百度apollo的控制节点conrol也是使用同样的思路。

如果对自动驾驶算法感兴趣，可以关注我的主页和专栏。

https://blog.csdn.net/nn243823163/category_11685852.htmlhttps://blog.csdn.net/nn243823163/category_11685852.html最新文章推荐：

Apollo Planning决策规划算法代码详细解析 (1)：Scenario选择

Apollo Planning决策规划算法代码详细解析 (5)：规划算法流程介绍

Apollo Planning决策规划算法代码详解 (22):决策规划算法最完整介绍

自动驾驶算法详解(2): prescan联合simulink进行FCW的仿真

自动驾驶算法详解(3): LQR算法进行轨迹跟踪，lqr_speed_steering_control( )的python实现

自动驾驶算法详解(5): 贝塞尔曲线进行路径规划的python实现

Apollo算法仿真调试(1): 使用Vscode断点调试apollo的方法

Apollo规划决策算法仿真调试(4): 动态障碍物绕行

Apollo规划决策算法仿真调试(7):pnc_map模块详解GetRouteSegments规划局部地图生成下篇_

正文如下：

一、横向LQR问题模型建立：

理论部分比较成熟，这里只介绍demo所使用的建模方程：

使用离散代数黎卡提方程求解

系统状态矩阵与LQR同时控制横纵向相比有所简化，状态矩阵如下，X = [距离差，距离差导数，角度差，角度差导数]：

输入矩阵变为1个变量，只有前轮转角。

A矩阵和B矩阵如下：

二、纵向PID控制

纵向上由PID算法来计算加速度，本demo中只保留P项：

三、结果分析

从状态更新的方法可以看到，纵向控制的速度会影响横向控制的结果

1、纵向参数P = 1 时的控制结果：

速度控制结果：

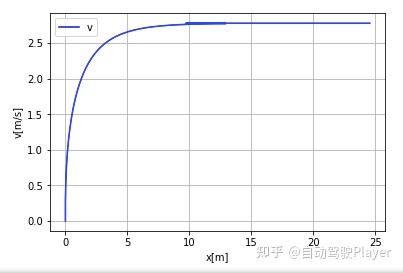
轨迹跟踪结果：

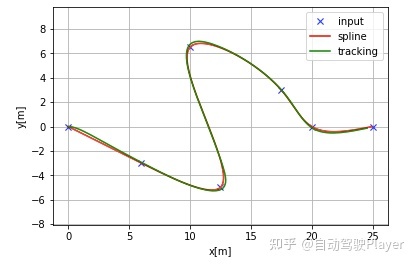
2、纵向参数P = 5 时的控制结果：

速度控制结果：

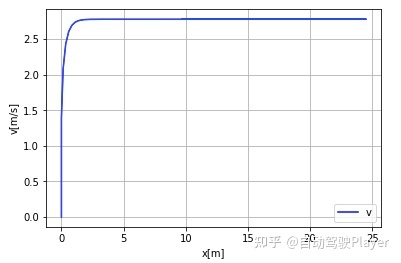
轨迹跟踪结果：

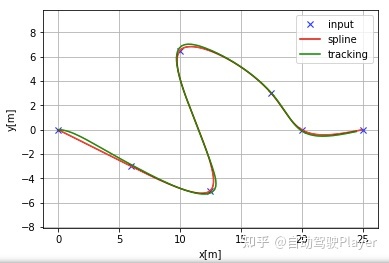
3、纵向参数P = 20时的控制结果：

速度控制结果：

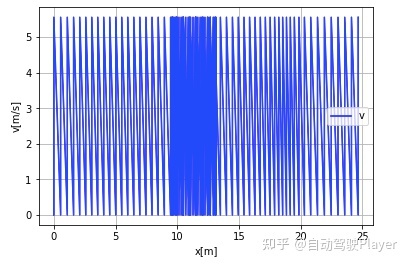
轨迹跟踪结果：

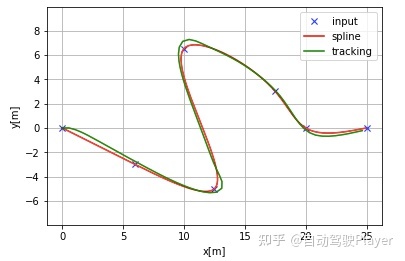
4、纵向参数P = 30时的控制结果：

速度控制结果：

四、代码实现

1、参数初始化

Kp = 1.0 # speed proportional gain


# LQR parameter
Q = np.eye(4)
R = np.eye(1)


# parameters
dt = 0.1 # time tick[s]
L = 0.5 # Wheel base of the vehicle [m]
max_steer = np.deg2rad(45.0) # maximum steering angle[rad]


show_animation = True
#  show_animation = False

2、相关函数定义

def PIDControl(target, current):
    a = Kp * (target - current)
 return a



def lqr_steering_control(state, cx, cy, cyaw, ck, pe, pth_e):
    ind, e = calc_nearest_index(state, cx, cy, cyaw)


    k = ck[ind]
    v = state.v
    th_e = pi_2_pi(state.yaw - cyaw[ind])


    A = np.zeros((4, 4))
    A[0, 0] = 1.0
    A[0, 1] = dt
    A[1, 2] = v
    A[2, 2] = 1.0
    A[2, 3] = dt
 # print(A)


    B = np.zeros((4, 1))
    B[3, 0] = v / L


    K, _, _ = dlqr(A, B, Q, R)


    x = np.zeros((4, 1))


    x[0, 0] = e
    x[1, 0] = (e - pe) / dt
    x[2, 0] = th_e
    x[3, 0] = (th_e - pth_e) / dt


    ff = math.atan2(L * k, 1)
    fb = pi_2_pi((-K @ x)[0, 0])


    delta = ff + fb


 return delta, ind, e, th_e



def closed_loop_prediction(cx, cy, cyaw, ck, speed_profile, goal):
    T = 500.0 # max simulation time
    goal_dis = 0.3
    stop_speed = 0.05


    state = State(x=-0.0, y=-0.0, yaw=0.0, v=0.0)


    time = 0.0
    x = [state.x]
    y = [state.y]
    yaw = [state.yaw]
    v = [state.v]
    t = [0.0]


    e, e_th = 0.0, 0.0


 while T >= time:
        dl, target_ind, e, e_th = lqr_steering_control(
            state, cx, cy, cyaw, ck, e, e_th)


        ai = PIDControl(speed_profile[target_ind], state.v)
        state = update(state, ai, dl)


 if abs(state.v) <= stop_speed:
            target_ind += 1


        time = time + dt


 # check goal
        dx = state.x - goal[0]
        dy = state.y - goal[1]
 if math.hypot(dx, dy) <= goal_dis:
 print("Goal")
 break


        x.append(state.x)
        y.append(state.y)
        yaw.append(state.yaw)
        v.append(state.v)
        t.append(time)


 if target_ind % 100 == 0 and show_animation:
            plt.cla()
 # for stopping simulation with the esc key.
            plt.gcf().canvas.mpl_connect('key_release_event',
 lambda event: [exit(0) if event.key == 'escape' else None])
            plt.plot(cx, cy, "-r", label="course")
            plt.plot(x, y, "ob", label="trajectory")
            plt.plot(cx[target_ind], cy[target_ind], "xg", label="target")
            plt.axis("equal")
            plt.grid(True)
            plt.title("speed[km/h]:" + str(round(state.v * 3.6, 2))
 + ",target index:" + str(target_ind))
            plt.pause(0.0001)


 return t, x, y, yaw, v

3、主函数

def main():
 print("LQR steering control tracking start!!")
#     ax = [0.0, 6.0, 12.5, 10.0, 7.5, 3.0, -1.0]
#     ay = [0.0, -3.0, -5.0, 6.5, 3.0, 5.0, -2.0]


    ax = [0.0, 6.0, 12.5, 10.0, 17.5, 20.0, 25.0]
    ay = [0.0, -3.0, -5.0, 6.5, 3.0, 0.0, 0.0]
 
    goal = [ax[-1], ay[-1]]


    cx, cy, cyaw, ck, s = calc_spline_course(
        ax, ay, ds=0.1)
    target_speed = 10.0 / 3.6 # simulation parameter km/h -> m/s


    sp = calc_speed_profile(cx, cy, cyaw, target_speed)


    t, x, y, yaw, v = closed_loop_prediction(cx, cy, cyaw, ck, sp, goal)


 if show_animation: # pragma: no cover
        plt.close()
        plt.subplots(1)
        plt.plot(ax, ay, "xb", label="input")
        plt.plot(cx, cy, "-r", label="spline")
        plt.plot(x, y, "-g", label="tracking")
        plt.grid(True)
        plt.axis("equal")
        plt.xlabel("x[m]")
        plt.ylabel("y[m]")
        plt.legend()
 
        plt.show()