概述
| 目录 | 滑模控制的一点笔记和看法 |
|---|---|
| 1 | 【控制】滑动模型控制（Sliding Mode Control） |
| 2 | 【控制】滑模控制，小例子，有程序有结果图 |
| 3 | 【控制】滑模控制，滑模面的选择 |
文章目录
- 1 问题描述
- 2 滑模控制器设计
- 2.1 滑模面选择
- 2.2 控制器设计
- 2.3 稳定性证明
- 3 实验验证
- 3.1 单纯滑模面控制
- 3.2 饱和函数替换符号函数
- Ref.
1 问题描述
假设存在一个被控系统如下
x
˙
1
=
x
2
x
˙
2
=
x
3
x
˙
3
=
x
1
+
x
2
x
3
+
u
(1)
begin{aligned} dot{x}_1 &= x_2 \ dot{x}_2 &= x_3 \ dot{x}_3 &= x_1 + x_2 x_3 + u \ end{aligned} tag{1}
x˙1x˙2x˙3=x2=x3=x1+x2x3+u(1)
2 滑模控制器设计
接下来设计其滑模控制器
2.1 滑模面选择
设计滑模面为
s
=
x
3
+
2
x
2
+
x
1
(2)
s = x_3 + 2 x_2 + x_1 tag{2}
s=x3+2x2+x1(2)
2.2 控制器设计
对切换函数
s
s
s 求导有
s
˙
=
x
˙
3
+
2
x
˙
2
+
x
˙
1
=
x
1
+
x
2
x
3
+
u
+
2
x
3
+
x
2
=
x
1
+
x
2
+
2
x
3
+
x
2
x
3
+
u
(3)
begin{aligned} dot{s} &= dot{x}_3 + 2 dot{x}_2 + dot{x}_1 \ &= x_1 + x_2 x_3 + u + 2 x_3 + x_2 \ &= x_1 + x_2 + 2 x_3 + x_2 x_3 + u end{aligned} tag{3}
s˙=x˙3+2x˙2+x˙1=x1+x2x3+u+2x3+x2=x1+x2+2x3+x2x3+u(3)
取指数趋近律有
s
˙
=
−
sgn
(
s
)
−
s
(4)
dot{s} = -text{sgn}(s) - s tag{4}
s˙=−sgn(s)−s(4)
可得控制器
u
u
u 为
s
˙
=
−
sgn
(
s
)
−
s
=
x
1
+
x
2
+
2
x
3
+
x
2
x
3
+
u
u
=
−
sgn
(
s
)
−
s
−
x
1
−
x
2
−
2
x
3
−
x
2
x
3
(5)
begin{aligned} dot{s} &= -text{sgn}(s) - s = x_1 + x_2 + 2 x_3 + x_2 x_3 + u \ u &= -text{sgn}(s) - s - x_1 - x_2 - 2 x_3 - x_2 x_3 end{aligned} tag{5}
s˙u=−sgn(s)−s=x1+x2+2x3+x2x3+u=−sgn(s)−s−x1−x2−2x3−x2x3(5)
2.3 稳定性证明
取李雅普诺夫函数有
V
=
1
2
s
2
(6)
V = frac{1}{2} s^2 tag{6}
V=21s2(6)
求导有
V
˙
=
s
s
˙
=
s
(
−
sgn
(
s
)
−
s
)
=
−
sgn
(
s
)
s
−
s
2
=
−
(
∣
s
∣
+
s
2
)
≤
0
(7)
begin{aligned} dot{V} &= s dot{s} \ &= s (-text{sgn}(s) - s) \ &= -text{sgn}(s) s - s^2 \ &= -(|s| + s^2) le 0 end{aligned} tag{7}
V˙=ss˙=s(−sgn(s)−s)=−sgn(s)s−s2=−(∣s∣+s2)≤0(7)
因为李雅普诺夫函数的微分是负定的，那么系统渐进稳定，即 s s s 趋于0。又因为 s = x 3 + 2 x 2 + x 1 s = x_3 + 2 x_2 + x_1 s=x3+2x2+x1，因此 x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3 都会趋于0。
3 实验验证
3.1 单纯滑模面控制
单纯使用滑模面的控制会出现抖振现象，这一点也可以从下图中看出。
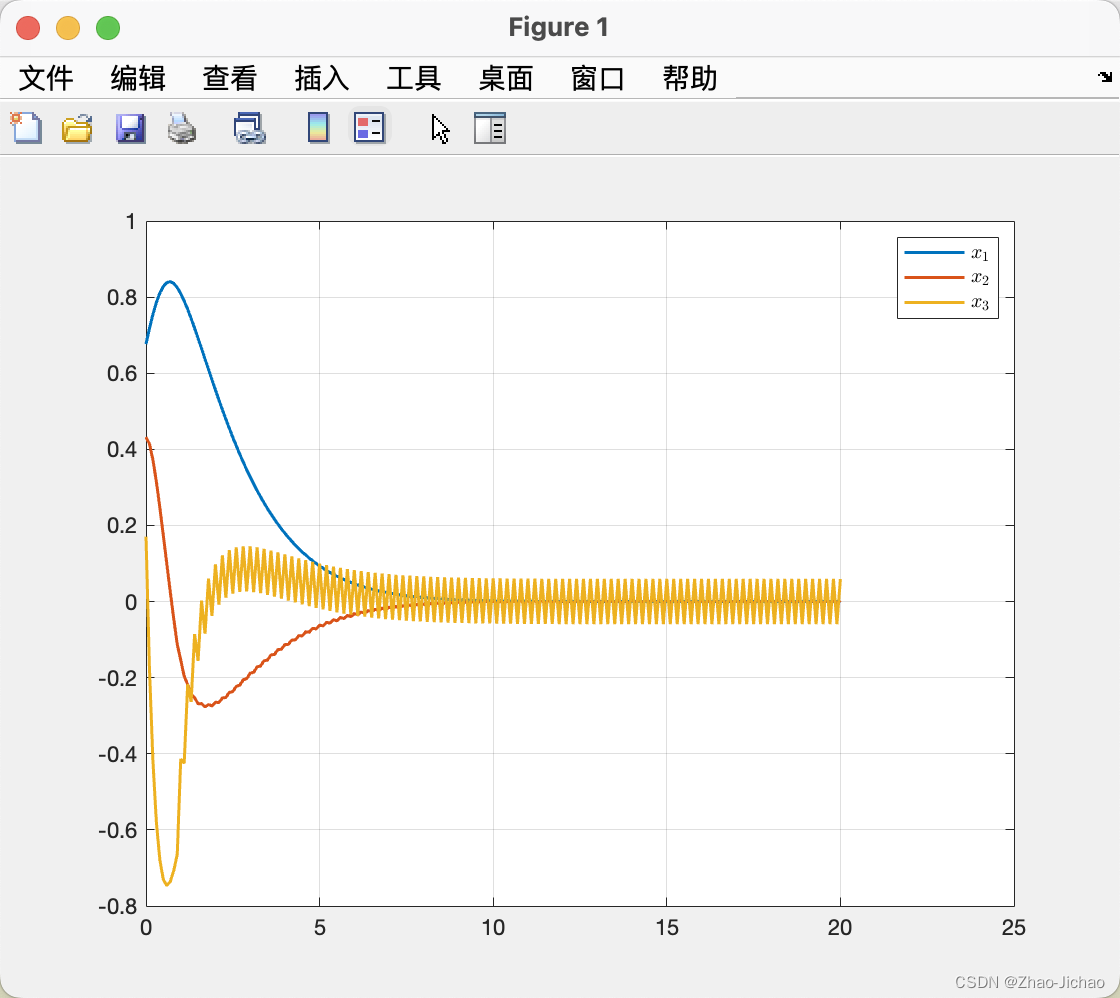
clear
clc
x_1(:,1) = rand;
x_2(:,1) = rand;
x_3(:,1) = rand;
%%
tBegin = 0;
tFinal = 20;
dT = 0.1;
times = (tFinal - tBegin) / dT;
t(1,1) = tBegin;
for k = 1:times
% record time
t(:,k+1) = t(:,k) + dT;
% slide model plane
s = x_3(:,k) + 2*x_2(:,k) + x_1(:,k);
% control input
u = -sign(s)-s-x_1(:,k)-x_2(:,k)-2*x_3(:,k)-x_2(:,k)*x_3(:,k);
% update states
dot_x_3 = x_1(:,k) + x_2(:,k) * x_3(:,k) + u;
x_3(:,k+1) = x_3(:,k) + dT * (x_1(:,k) + x_2(:,k) * x_3(:,k) + u);
dot_x_2 = x_3(:,k+1);
x_2(:,k+1) = x_2(:,k) + dT * dot_x_2;
dot_x_1 = x_2(:,k+1);
x_1(:,k+1) = x_1(:,k) + dT * dot_x_1;
end
%%
plot(t,x_1, t,x_2, t,x_3, 'linewidth',1.5);
legend('$x_1$', '$x_2$', '$x_3$', 'interpreter','latex');
grid on;
3.2 饱和函数替换符号函数
为了防止抖振，可以采用饱和函数 sat(s) 代替控制器中的符号函数sgn(s)。
在Matlab中没有相应的函数，因此我们写了个子函数来自己构建饱和函数，这一点可以在下边的代码里看到。
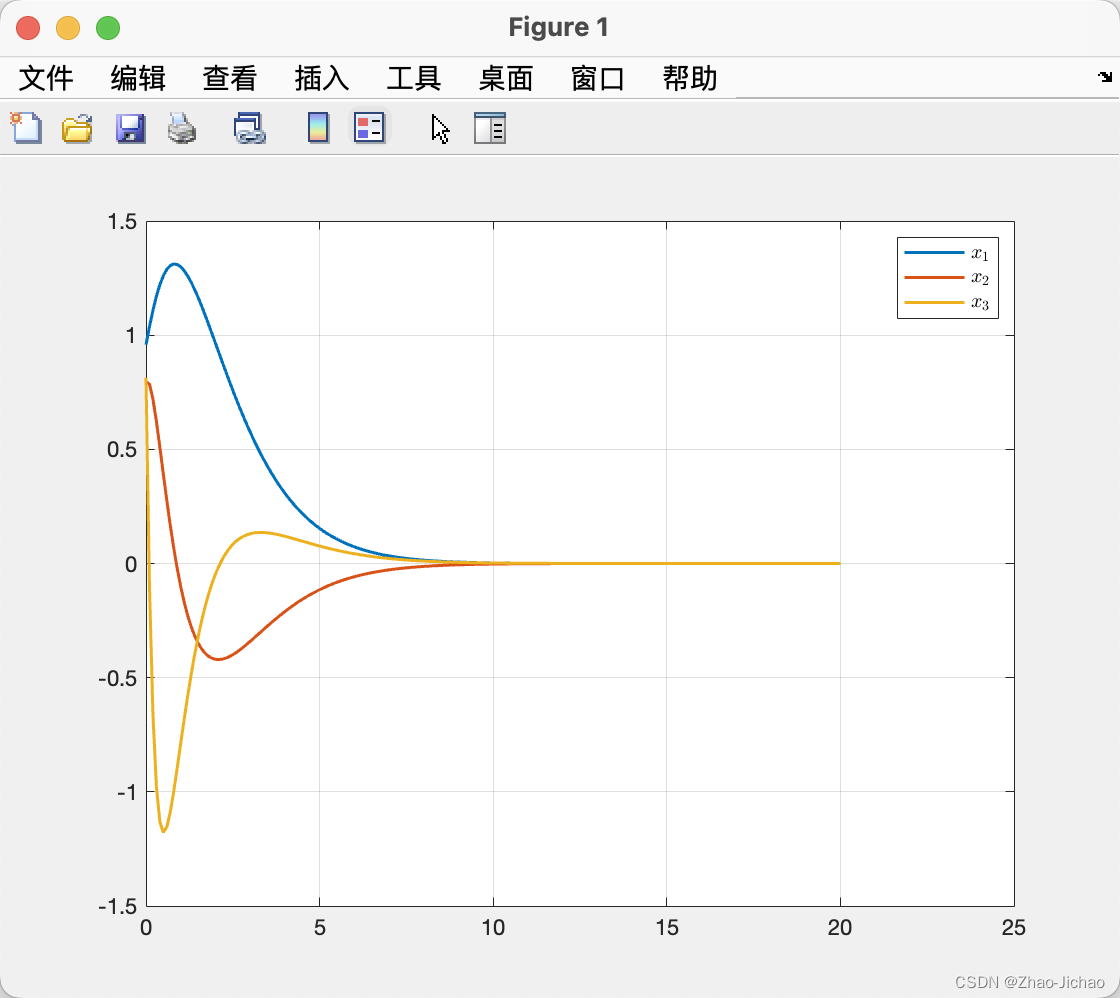
clear
clc
x_1(:,1) = rand;
x_2(:,1) = rand;
x_3(:,1) = rand;
%%
tBegin = 0;
tFinal = 20;
dT = 0.1;
times = (tFinal - tBegin) / dT;
t(1,1) = tBegin;
for k = 1:times
% record time
t(:,k+1) = t(:,k) + dT;
% slide model plane
s = x_3(:,k) + 2*x_2(:,k) + x_1(:,k);
% control input
u = -sat(s)-s-x_1(:,k)-x_2(:,k)-2*x_3(:,k)-x_2(:,k)*x_3(:,k);
% update states
dot_x_3 = x_1(:,k) + x_2(:,k) * x_3(:,k) + u;
x_3(:,k+1) = x_3(:,k) + dT * (x_1(:,k) + x_2(:,k) * x_3(:,k) + u);
dot_x_2 = x_3(:,k+1);
x_2(:,k+1) = x_2(:,k) + dT * dot_x_2;
dot_x_1 = x_2(:,k+1);
x_1(:,k+1) = x_1(:,k) + dT * dot_x_1;
end
%%
plot(t,x_1, t,x_2, t,x_3, 'linewidth',1.5);
legend('$x_1$', '$x_2$', '$x_3$', 'interpreter','latex');
grid on;
%%
function out = sat(s)
sMax = 10;
sMin = -10;
out = s;
if s > sMax
out = sMax;
end
if s < sMin
out = sMin;
end
end
Ref.
- 基于准滑动模态的滑模控制实例（采用饱和函数sat(s)代替符号函数）
最后
以上就是勤恳黄豆为你收集整理的【控制】滑模控制，小例子，有程序有结果图1 问题描述2 滑模控制器设计3 实验验证Ref.的全部内容，希望文章能够帮你解决【控制】滑模控制，小例子，有程序有结果图1 问题描述2 滑模控制器设计3 实验验证Ref.所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
![[滑模控制器浅述] （1） 二阶系统的简单滑模控制器设计[滑模控制器浅述] （1） 二阶系统的简单滑模控制器设计](/uploads/reation/bcimg9.png)
发表评论 取消回复