这是Java大数源码剖析系列的第二篇文章, 上一篇文章是
Java大数源码剖析(一) - BigInteger的底层数据结构
BigInteger提供的加减操作
- 加法 :
public BigInteger add(BigInteger val), 将返回本身加上val的结果 - 减法 :
public BigInteger subtract(BigInteger val), 返回本身减去val的结果
使用示例
public class Test {
public static void main(String[] args) {
BigInteger a = new BigInteger("1234567654321");
BigInteger b = new BigInteger("7654321234567");
BigInteger c = a.add(b);
BigInteger d = a.subtract(b);
BigInteger e = b.subtract(a);
System.out.printf("%s + %s = %sn", a, b, c);
System.out.printf("%s - %s = %sn", a, b, d);
System.out.printf("%s - %s = %sn", b, a, e);
}
}
输出结果 :
1234567654321 + 7654321234567 = 8888888888888
1234567654321 - 7654321234567 = -6419753580246
7654321234567 - 1234567654321 = 6419753580246
实现思路
JDK对BigInteger加减法的实现思路是将两个整数的加减法转换成正整数的加减法, 具体如下 :
| a | op | b | 备注 | 操作方法 |
|---|---|---|---|---|
| 正/负 | + | 正/负 | a, b同号 | 将a, b的绝对值相加, 结果的符号标志等于操作数的符号标志 |
| 正/负 | + | 负/正 | a, b异号 | 比较a, b绝对值的大小, 计算出大的绝对值减去小的绝对值 的差即为结果的绝对值, 结果的符号标志很容易得到 |
| 正/负 | - | 正/负 | a, b同号 | 比较a, b绝对值的大小, 计算出大的绝对值减去小的绝对值 的差即为结果的绝对值, 结果的符号标志很容易得到 |
| 正/负 | - | 负/正 | a, b异号 | 将a, b的绝对值相加, 结果的符号标志等于a的符号标志 |
根据上面的分析, 我们可以看出, 对于绝对值的加减法是实现大整数加减法的关键, 除此之外, 还要实现一个用来比较绝对值大小的方法. 对于绝对值的操作可以转换为对于mag数组的操作, 所以JDK源码提供三个方法, 分别是将mag数组按照二进制相加, 相减, 比较大小
源码剖析
-
mag数组相加 :
private static int[] add(int[] x, int[] y)-
基本思路是 :
-
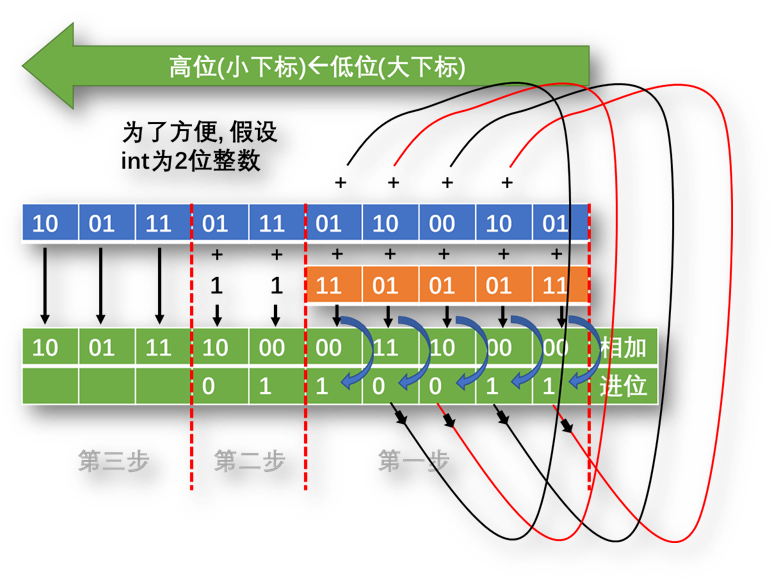
先将两个数组的从低位到高位(大端, 即从下标大者向下标小者)的共同部分逐int相加, 注意如果有进位, 保存下来, 加下一对int的时候加上进位.
-
根据加完共同部分后是否进位分别处理, 如果有则需要对mag较长者进一步处理, 从上一步处理到的int的高一个的int继续做加一操作, 注意保留进位, 直到没有进位或处理完数组为止.
-
将剩余的部分直接拷贝到结果数组, 如果最终还有进位, 在结果数组前面插入一个1 (扩展一个int)
-
-
-
为了方便处理和判断进位, 在加之前将int转换成了long.
- 注意, 由于int是直接当做32位二进制使用的, 也就是说, 这里的本来的作为符号位(补码)的int的最高位是没有符号位意义的, 被当做了不同的一位(由于Java没有无符号整数, 这里把int当做了无符号32位数).
-
也就是说int永远都是表示正数, 直接转换成long是不行的, 如果int最高位为1, 转换而来的long的高32位都会成为1(有符号扩展).
- 我们想要的是对int做无符号扩展成long, 也就高位直接补0, JDK的做法是定义一个
long LONG_MASK = 0xFFFFFFFF, 将一个int做无符号扩展就是其与LONG_MASK按位与的结果
- 我们想要的是对int做无符号扩展成long, 也就高位直接补0, JDK的做法是定义一个
-
将两个int都转无符号扩展为long再相加, 根据结果的第32位(从0开始)即可判断是否有进位, 如果有进位则此位为1, 反之为0
/**
* Adds the contents of the int arrays x and y. This method allocates
* a new int array to hold the answer and returns a reference to that
* array.
*/
// 将二进制数x和y相加
private static int[] add(int[] x, int[] y) {
// 保证x为较大者
if (x.length < y.length) {
int[] tmp = x;
x = y;
y = tmp;
}
int xIndex = x.length;
int yIndex = y.length;
int result[] = new int[xIndex];
long sum = 0;
if (yIndex == 1) { // 觉得没用, 都可以按照else的作法进行处理
sum = (x[--xIndex] & LONG_MASK) + (y[0] & LONG_MASK) ;
result[xIndex] = (int)sum;
} else {
// Add common parts of both numbers
while (yIndex > 0) { // 从低位向高位相加, 每次将上次的进位加上
sum = (x[--xIndex] & LONG_MASK) +
(y[--yIndex] & LONG_MASK) +
(sum >>> 32); // 如果有进位即sum的第32位为1 => sum >>> 32 == 1
result[xIndex] = (int)sum;
}
}
// Copy remainder of longer number while carry propagation is required
boolean carry = (sum >>> 32 != 0);
while (xIndex > 0 && carry) // 如果还有进位就将x剩下的位从低到高加一存到结果直到没有进
// 位或处理完x
carry = ((result[--xIndex] = x[xIndex] + 1) == 0);
// Copy remainder of longer number
while (xIndex > 0) // 拷贝剩余的位
result[--xIndex] = x[xIndex];
// Grow result if necessary
if (carry) { // 如果还有进位, 就要扩展result
int bigger[] = new int[result.length + 1];
System.arraycopy(result, 0, bigger, 1, result.length);
bigger[0] = 0x01; // 将最高位置1
return bigger; // 将扩展后的结果返回
}
return result;
}
-
mag数组相减 :
private static int[] subtract(int[] big, int[] little)-
基本思路和相加类似, 不同的是进位变成了借位
-
判断借位的思路是判断相减后的long类型右移32位后是否为0, 小于0则是有借位
/** * Subtracts the contents of the second int arrays (little) from the * first (big). The first int array (big) must represent a larger number * than the second. This method allocates the space necessary to hold the * answer. */ // 将二进制数big和little相减, big > little private static int[] subtract(int[] big, int[] little) { // big一定要大于little int bigIndex = big.length; int result[] = new int[bigIndex]; int littleIndex = little.length; long difference = 0; // Subtract common parts of both numbers while (littleIndex > 0) { // 自低位向高位作减法 difference = (big[--bigIndex] & LONG_MASK) - (little[--littleIndex] & LONG_MASK) + (difference >> 32); // 如果diff < 0 : diff >> 32 == -1 // 即上次有借位, 再多减一个1 result[bigIndex] = (int)difference; } boolean borrow = (difference >> 32 != 0); while (bigIndex > 0 && borrow) // 如果还有借位, 则让big的较高位减1直到没有借位 // 减1导致有借位只有一种情况即 0 - 1 == -1 (实际为0xFFFFFFFF) borrow = ((result[--bigIndex] = big[bigIndex] - 1) == -1); // 直接将big剩余的高位部分拷贝到结果数组 while (bigIndex > 0) result[--bigIndex] = big[bigIndex]; return result; } -
-
比较mag的数组的大小 :
final int compareMagnitude(BigInteger val)/** * Compares the magnitude array of this BigInteger with the specified * BigInteger's. This is the version of compareTo ignoring sign. * * @param val BigInteger whose magnitude array to be compared. * @return -1, 0 or 1 as this magnitude array is less than, equal to or * greater than the magnitude aray for the specified BigInteger's. */ // 比较this和val的mag数组表示的整数的大小(即比较的是绝对值的大小) final int compareMagnitude(BigInteger val) { int[] m1 = mag; int len1 = m1.length; int[] m2 = val.mag; int len2 = m2.length; if (len1 < len2) // 长度小者定为小者 return -1; if (len1 > len2) return 1; for (int i = 0; i < len1; i++) { // 从高位到低位比较 int a = m1[i]; int b = m2[i]; if (a != b) // 第一个不同的位小的定为小者 return ((a & LONG_MASK) < (b & LONG_MASK)) ? -1 : 1; } return 0; }利用上面三个方法就能实现大数的加减法
-
大数加法的实现 :
/** * Returns a BigInteger whose value is {@code (this + val)}. * * @param val value to be added to this BigInteger. * @return {@code this + val} */ // 大数相加 public BigInteger add(BigInteger val) { if (val.signum == 0) // 如果val是0直接返回自己(a + 0 == b) return this; if (signum == 0) // 如果自己是0直接返回val(0 + b == a) return val; if (val.signum == signum) // 如果两者同号, 调用 static int[] add(int[], int[]) // 直接将两者的mag相加 return new BigInteger(add(mag, val.mag), signum); // 下面是处理两者异号的情况, 将加法转换为减法 int cmp = compareMagnitude(val); // 比较this和val的mag的大小(实际就是 // 比较两者绝对值的大小) if (cmp == 0) // 如果两者绝对值相等, 结果为0 // public static final BigInteger ZERO = new BigInteger(new int[0], 0); return ZERO; int[] resultMag = (cmp > 0 ? subtract(mag, val.mag) // 否则, 调用subtract : subtract(val.mag, mag)); // 将二者的绝对值作差 resultMag = trustedStripLeadingZeroInts(resultMag); // 去除高位的所有0 return new BigInteger(resultMag, cmp == signum ? 1 : -1); // 构造结果 } -
大数减法的实现 :
/** * Returns a BigInteger whose value is {@code (this - val)}. * * @param val value to be subtracted from this BigInteger. * @return {@code this - val} */ // 大数相减 public BigInteger subtract(BigInteger val) { if (val.signum == 0) // val为0, 返回自己 return this; if (signum == 0) // 自己为0, 返回val的相反数 return val.negate(); if (val.signum != signum) // 如果异号, 即转化为正数加法 return new BigInteger(add(mag, val.mag), signum); // 下面是处理同号情况, 同号则利用正数减法 int cmp = compareMagnitude(val); if (cmp == 0) // 如果两者绝对值相等, 结果为0 return ZERO; int[] resultMag = (cmp > 0 ? subtract(mag, val.mag) // 绝对值大减小 : subtract(val.mag, mag)); resultMag = trustedStripLeadingZeroInts(resultMag); // 去除高位的所有0 // 结果的正负号是同号减法操作数的正负和其绝对值相减结果的正负的共同作用的结果 // 设 a = sig * |a|, b = sig * |b| // 则 a - b <=> sig * (|a| - |b|) // 则 SIG(a - b) <=> sig * SIG(|a| - |b|) , SIG(N)表示N的正负号 // this正负标志 绝对值相减结果的正负标志 => 结果正负标志 // 1 1 1 // 1 -1 -1 // -1 1 -1 // -1 -1 1 // => result.signum = cmp == signum ? 1 : -1 (cmp * signum) return new BigInteger(resultMag, cmp == signum ? 1 : -1); }大数加减法的时间复杂度都为
O(max(n, m)), 这里n和m分别是两个加数的mag数组的长度, 进一步可以推出时间复杂度为O(max(nn, mm) / 32), 这里的nn和mm分别是两个加数的二进制位的多少。如果采用string存放大整数,一个char存放一个十进制位,也就是相当于上述mag数组的数组元素类型由32位整数变为了4位无符号整数(严格说来 l o g 2 10 log_210 log210位), 时间复杂度就变成了
O(max(nn, mm) / 4)显然大了不少.
最后
以上就是朴素小刺猬最近收集整理的关于Java大数源码剖析(二) - BigInteger的加减操作的全部内容,更多相关Java大数源码剖析(二)内容请搜索靠谱客的其他文章。






![记录BigInteger的两个构造方法构造方法: BigInteger(byte[] val)构造方法: BigInteger(int signum, byte[] magnitude)](https://file2.kaopuke.com:8081/files_image/reation/bcimg10.png)

发表评论 取消回复