1. 触发器具有哪些基本特征?
答:
触发器的基本特征:
(1)有两个稳态,可分别表示二进制数码0和1无外触发时可维持稳态;
(2)外触发下,两个稳态可相互转换(称翻转),已转换的稳定状态可长期保持下来,这就使得触发器能够记忆二进制信息,常用作二进制存储单元。
2. 用与非门组成的基本RS触发器的有效输入信号为哪种形式? 对输入信号有哪些约束?
答:
有效输入信号为低电平或负脉冲。
不允许输入端R、S同时为“0”(即不允许同时为低电平或者负脉冲)。
3. 用或非门组成的基本RS触发器的有效输入信号为哪种形式? 对输入信号有哪些约束?
答:
有效输入信号为高电平或者正脉冲。
不允许输入端R、S同时为“1”(即不允许同时为高电平或者正脉冲)。
4. 触发器的逻辑功能通常采用哪些方式进行描述?
答:
描述触发器的逻辑功能有三种方法:
特性表
特性方程
状态转换图
5. 试写出用与非门组成的基本 RS 触发器的次态方程和约束方程。
答:
利用
R
、
S
mathrm{R} 、 mathrm{~S}
R、 S 不允许同时为 0 的约束条件, 化简后可得到该触发器的次态方程为
Q
n
+
1
=
S
‾
+
R
Q
mathrm{Q}^{n+1}=overline{mathrm{S}}+mathrm{RQ}
Qn+1=S+RQ
因为
R
、
S
R 、 S
R、S 不允许同时为 0, 所以输人必须满足约束方程:
R
+
S
=
1
mathrm{R}+mathrm{S}=1
R+S=1
6. 试写出用或非门组成的基本 RS 触发器的次态方程和约束方程。
答:
利用
R
、
S
mathrm{R} 、 mathrm{~S}
R、 S 不允许同时为 1 的约束条件, 化简后可得到该触发器的次态方程和约束方 程为
Q
n
+
1
=
S
+
R
‾
Q
(次态方程)
R
S
=
0
(约束方程)
begin{array}{l} mathrm{Q}^{n+1}=mathrm{S}+overline{mathrm{R}} mathrm{Q} text { (次态方程) } \ mathrm{RS}=0 text { (约束方程) } end{array}
Qn+1=S+RQ (次态方程) RS=0 (约束方程)
7. 钟控 RS 触发器和用或非门组成的基本 RS 触发器有哪些异同?
答:
尽管简单钟控 RS 触发器的功能描述在形式上与由或非门构成的基本 RS触发器 完全相同, 但由或非门构成的基本
R
S
R S
RS 触发器的状态变化直接受输入信号
R
、
S
R 、 S
R、S 的影 响, 而钟控
R
S
R S
RS 触发器的状态变化仅当时钟控制信号
C
P
=
1
C P=1
CP=1 时才受输入信号
R
、
S
R 、 S
R、S 的 影响, 当时钟控制信号
C
P
=
0
mathrm{CP}=0
CP=0 时, 触发器状态保持不变。此外, 钟控
R
S
mathrm{RS}
RS 触发器虽 然解决了对触发器工作进行定时控制的问题, 而且具有结构简单的优点, 但输入信 号依然存在约束条件, 即
R
、
S
R 、 S
R、S 不能同时为 1 。
8. 试写出 D 触发器、T 触发器和JK触发器的次态方程。
答:
D触发器的次态方程:
Q
n
+
1
=
D
mathrm{Q}^{n+1}=mathrm{D}
Qn+1=D
T触发器的次态方程:
Q
n
+
1
=
T
Q
‾
+
T
‾
Q
=
T
⊕
Q
mathrm{Q}^{n+1}=mathrm{T}overline{ mathrm{Q}}+overline{mathrm{T}} mathrm{Q}=mathrm{T} oplus mathrm{Q}
Qn+1=TQ+TQ=T⊕Q
JK触发器的次态方程:
Q
n
+
1
=
J
Q
‾
+
K
‾
Q
mathrm{Q}^{n+1}=mathrm{J}overline{ mathrm{Q}}+overline{mathrm{K}} mathrm{Q}
Qn+1=JQ+KQ
9. 触发器的 “空翻” 现象是指什么? 产生空翻的原因是什么?
答:
“空翻” 是指在同一个时钟脉冲作用期间触发器状态发生两次或两次以上变化的现象。引起空翻的原因是在时钟脉冲为高电平期间, 输入信号的变化直接控制着触发器状态的变化。
10. 在图 5.24 5.24 5.24 (a) 所示的触发器电路中, 若输入端 D 的波形如图 5.24 5.24 5.24 (b) 所示, 试画出输出端 Q mathrm{Q} Q 的波形图 (设触发器初态为 0 )。
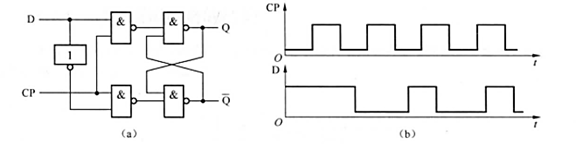
答:
输出端Q的波形图为:
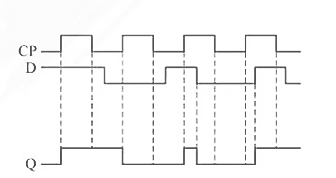
11. 已知时钟信号 C P mathrm{CP} CP与输入信号 A mathrm{A} A 和 B 的波形如图 5.25 5.25 5.25 (a) 所示, 试画出图 5.25 ( b ) 5.25(mathrm{~b}) 5.25( b) 、图 5.25 ( c ) 5.25(mathrm{c}) 5.25(c) 所示的两个逻辑电路中触发器 Q mathrm{Q} Q 端的输出波形图,设触发器初态为 0 。
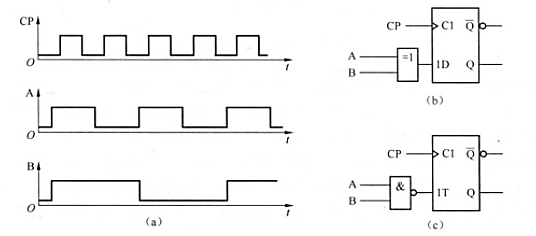
答:
触发器Q端的输出波形图为:
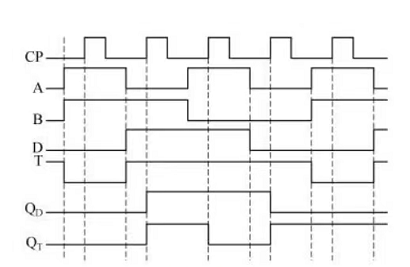
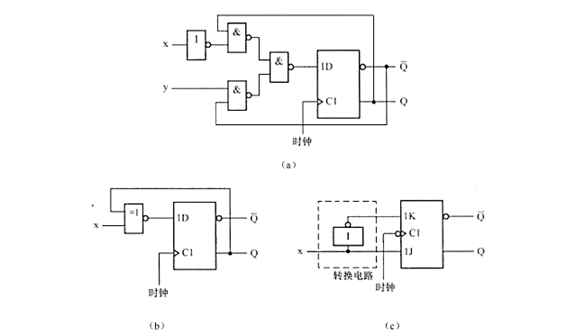
12. 分析图 5.26 5.26 5.26 所示 3 个逻辑电路, 说明各实现何功能。
答:
(1) 图(a) 所示钟控
D
mathrm{D}
D 触发器的次态方程为:
Q
n
+
1
=
D
=
K
‾
Q
‾
⋅
J
‾
=
K
‾
Q
+
J
Q
‾
mathrm{Q}^{mathrm{n}+1}=mathrm{D}=overline{overline{mathrm{K}} mathrm{Q}} cdot overline{mathrm{J}}=overline{mathrm{K}} mathrm{Q}+mathrm{J} overline{mathrm{Q}}
Qn+1=D=KQ⋅J=KQ+JQ, 由此可见该电路实现了
J
K
mathrm{JK}
JK 触发器的功能。
(2) 图 (b) 所示钟控
D
mathrm{D}
D 触发器的次态方程为:
Q
n
+
1
=
D
=
x
⊕
Q
‾
=
x
‾
Q
+
x
Q
‾
mathrm{Q}^{mathrm{n}+1}=mathrm{D}=overline{mathrm{x} oplus mathrm{Q}}=overline{mathrm{x}} mathrm{Q}+mathrm{x} overline{mathrm{Q}}
Qn+1=D=x⊕Q=xQ+xQ, 由此可见该电路实现了
T
mathrm{T}
T 触发器的功能。
(3) 图 (c)所示钟控
J
K
mathrm{JK}
JK 触发器的次态方程为:
Q
n
+
1
=
J
Q
‾
+
K
‾
Q
=
x
Q
‾
+
x
Q
‾
=
x
Q
‾
+
mathrm{Q}^{mathrm{n}+1}=mathrm{J} overline{mathrm{Q}}+overline{mathrm{K}} mathrm{Q}=mathrm{x} overline{mathrm{Q}}+overline{mathrm{xQ}}=mathrm{x} overline{mathrm{Q}}+
Qn+1=JQ+KQ=xQ+xQ=xQ+
x
Q
=
x
mathrm{xQ}=mathrm{x}
xQ=x, 由此可见该电路实现了
D
mathrm{D}
D 触发器的功能。
最后
以上就是缥缈小蘑菇最近收集整理的关于数字电路逻辑设计_第三版_微课版_第五章思考题与练习题(附答案)的全部内容,更多相关数字电路逻辑设计_第三版_微课版_第五章思考题与练习题(附答案)内容请搜索靠谱客的其他文章。








发表评论 取消回复