决策树

决策树（decision tree）是一种基本的分类与回归方法，此处主要讨论分类的决策树。

决策树学习的算法通常是一个递归地选择最优特征(选择方法的不同，对应着不同的算法)，并根据该特征对训练数据进行分割，使得各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分，也对应着决策树的构建。下面为一个实例图：

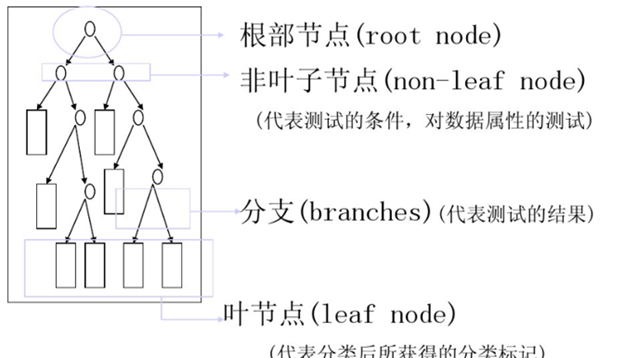
构造流程：

1） 开始：构建根节点，将所有训练数据都放在根节点，选择一个最优特征，按着这一特征将训练数据集分割成子集，使得各个子集有一个在当前条件下最好的分类。

2） 如果这些子集已经能够被基本正确分类，那么构建叶节点，并将这些子集分到所对应的叶节点去。

3）如果还有子集不能够被正确的分类，那么就对这些子集选择新的最优特征，继续对其进行分割，构建相应的节点，如果递归进行，直至所有训练数据子集被基本正确的分类，或者没有合适的特征为止。

4）每个子集都被分到叶节点上，即都有了明确的类，这样就生成了一颗决策树。

决策树的特点：

优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。
缺点：可能会产生过度匹配的问题
适用数据类型：数值型和标称型

其中常用的分类树算法有ID3、C4.5、CART

下面是一些信息论的知识

l 信息熵(information entropy)

熵(entropy)是表示随机变量不确定性的度量，设X是一个取有限值的离散随机变量，其概率分布为：

则随机变量X的熵定义为：

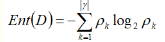
熵越大，随机变量的不确定性越大；也就是H(X)越小，随机变量的X的纯度越高。

l 信息增益(information gain)

训练数据集D采用特征a进行划分之后的信息增益Gain(D,a)为:

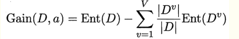
其中

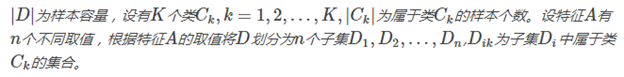
l 信息增益率(information gain
ratio)

特征a对训练数据集D的信息增益Gain_ratio(D,a)定义为其信息增益Gain(D,a)与训练数据集D关于特征a的值的熵IV(a)之比，即

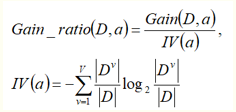
其中

代表以属性a进行划分，第V类的子集数量。

l 基尼指数(Gini index)

基尼指数Gini(D)表示集合D不确定性，基尼指数Gini(D,a)表示集合D经A=a分割后的不确定性(类似于熵)，基尼指数越小，样本的不确定性越小。分类问题中，假设有K个类，样本点属于第k类的概率为pk,则概率分布的基尼指数定义为

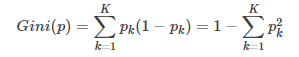
显然，Gini反映了在样本中随机抽取两个样本，其标记不一样的概率，因此基尼指数越小，数据集D的纯度越高。也就是说选择使得划分后基尼指数最小的属性作为最有划分属性。例如对于属性a，其基尼指数为：

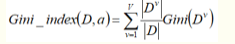
下面分别阐述ID3、C4.5、CART算法

1. ID3算法（基于信息增益作为属性选择的度量）
   基本思想：对于含有多个特征和类别标签的的数据集，利用信息增益作为选取特征的指标，进而选取出划分数据集最好的特征。
   算法流程在这里不做阐述。
   缺点：
   ID3算法只有树的生成, 所以该算法生成的树容易产生过拟合；
   ID3算法本身并未给出处理连续数据的方法；
   ID3算法不能处理带有缺失值的数据集, 故在算法挖掘之前需要对数据集中的缺失值进行预理；
   使用ID3算法构建决策树时, 若出现各属性值取值数分布偏差大的情况, 分类精度会大打折扣。

剪枝处理：剪枝是决策树学习算法对付"过拟合"的主要手段。

过拟合原因：

1）噪声导致的过拟合：拟合了被误标记的样例，导致误分类。

2）缺乏代表性样本导致的过拟合：缺乏代表性样本的少量训练集作出的决策会出现过拟合。

3）多重比较造成的过拟合：复杂模型。

基本策略有"预剪枝" 和"后剪枝"；

预剪枝是指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点；

后剪枝则是先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。

判断决策树泛化性能是否提升：留出法，即预留一部分数据用作"验证集"以进行性能评估。

例如：在预剪枝中，对于每一个分裂节点，对比分裂前后决策树在验证集上的预测精度，从而决定是否分裂该节点。而在后剪枝中，考察非叶节点，对比剪枝前后决策树在验证集上的预测精度，从而决定是否对其剪枝。

两种方法对比：

1）预剪枝使得决策树的很多分支都没有"展开”，不仅降低过拟合风险，而且显著减少训练/测试时间开销；但，有些分支的当前划分虽不能提升泛化性能，但在其基础上进行的后续划分却有可能导致性能显著提高，即预剪枝基于"贪心"本质禁止这些分支展开，给预剪枝决策树带来了欠拟含的风险。

2）后剪枝决策树通常比预剪枝决策树保留了更多的分支。一般情形下，后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝决策树，但后剪枝过程是在生成完全决策树之后进行的，并且要自底向上地对树中的所有非叶结点进行逐一考察，因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多。

对于剪枝内容补充，博客网址：https://blog.csdn.net/xo3ylAF9kGs/article/details/78623265

对于回归树以后再进行补充。

最后

以上就是忐忑仙人掌为你收集整理的决策树的全部内容，希望文章能够帮你解决决策树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。