[数据分析] 决策树算法：决策树的概念

1. 什么是决策树

顾名思义，决策树将以树状结构表现出来，被用来辅助作出决策。

具体结合例子来说，我们平时做决策时大多会伴随着层层的选择，比如找房子的时候，会考虑离工作/上课地点的距离、大小和价格、光照等等因素。
如果一个房子通勤快、价格低、光照好、空间大（虽然不太可能存在，但是只要存在这种房子）我们一定会作出“买/租”的决策。将我们作出这一决策的思考过程/选择过程以层次形式表现出来，如下：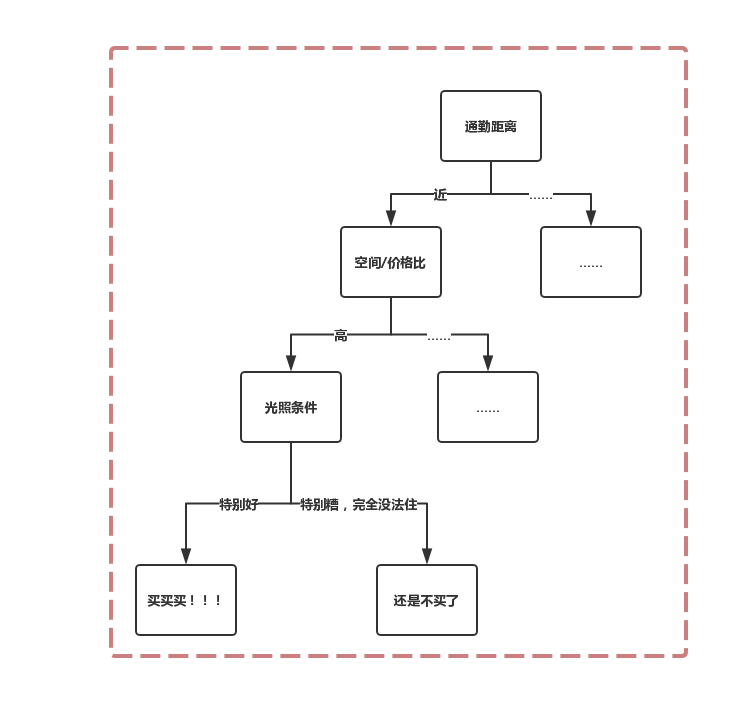
虽然我们平时并不一定会在决策的时候明显察觉到自己的决策符合这种结构。但许多决策/决定都可以被分解为这种结构。
比如：我们决定“如果明天不下雨，我们就去野炊。”
该决定可以分解为，以天气（是否下雨）作为结点，如果不下雨，就作出野炊的决定，如果下雨，就作出取消野炊的决定。

一般的，一棵决策树包含一个根结点、若干个内部结点和若干个叶结点；
叶结点对应于决策结果，其他每个结点则对应于一个属性测试；
每个结点包含的样本集合根据属性测试的结果被划分到子结点中；
根结点包含样本全集；
从根结点到每个叶结点的路径对应了一个判定测试序列。

2. 如何生成决策树

在对决策树是什么有一个总体认识之后，紧接着的要解决的问题就是，如何针对一个问题生成出该问题的决策树。
更准确地说，生成决策树要解决两个问题：

• 剪枝：如何选择用来分支决策的因素(即决策树的结点)；
• 构造：如何决定决策树结点的层次关系；

2.1剪枝

对决策树进行剪枝，就是剪去不必要的结点。
一来删去这些结点可能对决策树的判断没有多大的影响。则删去结点可以使得决策树更加简洁，进行决策的时候可以通过更少的判断得到不错的结果。
二来删去这些结点可能对决策树的效率明显的提高，可以通过更少的判断得到更好的结果。

剪枝可以分为“先剪枝”和“后剪枝”。
先剪枝是在构造决策树就对结点进行评估，如果结点的存在与否不影响决策树性能，则不对该结点再进行划分，使其称为叶结点，得出决策结论。
后剪枝是在构造完成决策树之后从叶结点开始对结点进行评估，如果删除结点对决策树性能没有影响，这删去该结点及其子树。
剪枝的目标是提高决策树的性能，如果决策树的性能不佳，可能出现过拟合或者欠拟合现象。

2.2 构造

在最开始的买房子的决策中，最先作为划分因素的是通勤距离。
然而可能通勤距离对你来说无关紧要。只要是价格低的，通勤距离近的你会买，通勤距离远的你也会买，那么最先拿价格来划分样本集，就很可能更快作出决策。所以，构造决策树的时候，要考虑的就是哪个结点作为根结点/内部结点/叶结点。
换言之，构造决策树就是在一个结点集合中不断地选出结点作为根结点（或者根结点子树的根结点）。第一个被选出来的结点就是整棵决策树的根结点。
之后选出内部结点（即子树的根结点）以及叶结点。

2.2.1 构造的依据

是什么让一个结点从结点集合中被我们选中，拎出来作为根结点的呢?
这就涉及到了我们选择结点的依据：纯度
通过决策树的形式，我们可以认为，
决策树就是对一个样本集合进行层层划分
于是，一个集合划分出的种类越少，可以认为这个集合中的样本差异越小，称之为纯度越高。
换言之，如果我们可以仅凭一个因素作出非黑即白决策（就像仅凭一个因素一个人是好是坏），则决策变得十分高效，我们自然会在需要作出决策的时候首先拿这个因素进行决策判断。
这就是为什么我们会将使得决策树纯度最高的结点最先挑出来作为根结点。

3. 构造的指标以及对应的算法

构造决策树的依据是纯度。
而用来衡量纯度的三个指标分别是：信息增益、信息增益率和基尼系数。
对应的三个算法是ID3算法、C4.5算法、Cart算法。

3.1 信息增益

ID3算法构造决策树（选择结点）的依据是信息增益。
信息增益最大的属性将优先被选择出来作为划分集合的结点。
信息增益指的是选择该属性作为结点所能得到的信息量。什么意思呢？这说的是从样本到决策结果存在不确定性，我们用信息熵衡量这种不确定性。如果作出一个选择之后得到了信息量，则信息熵下降。下降的值即为获得信息量的值，成为信息增益。
信息增益 = 选择结点前的信息熵 - 选择出结点后的信息熵

3.2 信息增益率

信息增益率 = 信息增益 / 属性熵
其说明的是信息熵下降了多少百分比。下降百分比最多的下降程度最大，优先选择作为结点。

3.3 基尼系数

基尼系数和信息熵一样，都是可以反映样本不确定度的指标。
基尼系数 = 1 - 各结果概率平方和
在被选择后能够使得基尼系数最小的属性，则可使得样本集合最稳定，不确定度最小。于是这样的结点将被优先选择出来作为结点。

最后

以上就是妩媚月饼为你收集整理的[数据分析] 决策树算法：决策树的概念的全部内容，希望文章能够帮你解决[数据分析] 决策树算法：决策树的概念所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。