1.常见的一些决策树
| 模型 | ID3 | C4.5 | CART |
| 结构 | 多叉树 | 多叉树 | 二叉树 |
| 特征选择 | 信息增益 | 信息增益率 | Gini系数、均方差 |
| 连续值处理 | 不支持 | 支持 | 支持 |
| 缺失值处理 | 不支持 | 支持 | 支持 |
| 剪枝 | 不支持 | 支持 | 支持 |
2.决策树树得构建流程
(1).首先构建根节点,将所有训练数据都放在根节点;
(2).选择一个最优特征,按照这一特征将训练集分割成子集,使得各个子集在当前条件下有一个最好的分类;
(3).如果子集非空,或者子集数量不小于最小数量,递归(1)(2)两步,直到所有子集都被正确分类或者没有合适的特征为止。
3.信息熵的计算方法
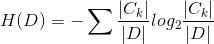
其中,D为数据全集,C为不同因变量类别k上的子集(传统意义上的y的类别)
4.信息增益计算方法
信息增益由两部分组成:1)信息熵;2)条件信息熵。
条件信息熵:在特征A给定条件下数据集D分类的不确定性,用公式表示如下:
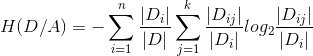
信息增益:知道特征A的信息而使得数据集D的不确定减少的程度:I(D,A) = H(D)-H(D/A)
也就是说:在特征A下找到最合适的切分,使得在该切分下信息量的变化最大,也就更加稳定;但是这个有一个问题,对于类别天生较多的特征,模型更容易选中,因为特征类别较多,切分后的信息增益天生更大,更容易满足我们的原始假设。
5. 信息增益率计算方法
在信息增益计算的基础不变的情况下增加了惩罚项:
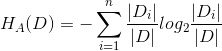
该惩罚项就是用划分的子集数上的熵来平衡了分类数过多的问题。
信息增益率的的计算公式如下:
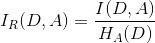
6.Gini系数
与熵一样,Gini基尼系数表征的也是事件的不确定性。
Gini系数二分情况下:
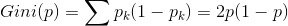
对于决策树样本D计算Gini系数:
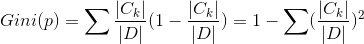
7.ID3的不足之处
- 存在偏向于选择取值较多的特征问题
- 不支持处理连续值
- 不支持处理缺省值
- 无法剪枝
8.C4.5相对于ID3的改进点
- 主动进行连续特征离散化
- 比如m个样本的连续特征A有m个,先set在order,再两两组合求中间值,以该值点作为划分的待选点
- 连续特征可以再后序特征划分中仍可继续参与计算
- 缺失问题优化
- 训练:用所有未缺失的样本,和之前一样,计算每个属性的信息增益,但是这里的信息增益需要乘以一个系数(未缺失样本/总样本)
- 预测:直接跳过该节点,并将此样本划入所有子节点,划分后乘以系数计算,系数为不缺失部分的样本分布
- 采用预剪枝
9.CART对连续特征处理的改进点
- 分类情况下的变量特征选择
- 离散变量:二分划分
- 连续变量:和C4.5处理方法一致,如果当前节点为连续属性,则该属性后面依旧可以参与子节点的产生选择过程
- 回归情况下
连续变量不再采用中间值划分,而是采用最小方差法
10.CART分类树建立算法的具体流程
算法从根节点开始,用训练集递归的建立CART树。
- 对于当前节点的数据集为D,如果样本个数小于阈值或者没有特征,则返回决策子树,当前节点停止递归
- 计算当前节点样本集D的基尼系数,如果基尼系数小于阈值,则返回决策树子树,当前节点停止递归
- 计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数
- 在计算出来的各个特征的各个特征值对数据集D的基尼系数中,选择基尼系数最小的特征A和对应的特征值a。根据这个最优特征和最优特征值,把数据集划分成两部分D1和D2,同时建立当前节点的左右节点,左节点的数据集D为D1,右节点的数据集D为D2
- 递归1~4
11.CART回归树建立算法的具体流程
构建的过程也是一样的,不同点在于在构建过程中遇到连续值的话,并不是利用C4.5中的中间值基尼系数的方式,而是采取了最小方差方法:
对于任意划分特征A,对应的任意划分点s两边划分成的数据集D1和D2,求出使D1和D2各自集合的均方差最小,同时D1和D2的均方差之和最小所对应的特征和特征值划分点,其中c1为D1的均值,c2为D2的均值:
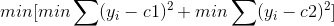
12.CART在分类和回归中输出的逻辑
- 回归树:利用最终叶子的均值或者中位数来作为输出结果
- 分类树:利用最终叶子的大概率的分类类别来作为输出结果
13.树形结构为何不需要归一化处理?
无论是分类树还是回归树,又或者是离散值或者连续值,树形结构每次都是找最优切分点划分的,不存在梯度导数等计算,数值缩放也不影响分裂点位置,对树模型的结构不造成影响,故不需要进行归一化。
14.决策树的优缺点
优点:
- 对特征的宽容程度高,可缺失可连续可离散
- 可解释性强
- 算法对数据没有强假设
- 可以解决线性及非线性问题
- 有特征选择等辅助功能
缺点:
- 处理关联性数据比较薄弱
- 对于各类别样本数量不一致的数据, 信息增益偏向于那些更多数值的特征
- 单棵树的拟合效果欠佳,容易过拟合
最后
以上就是霸气哈密瓜最近收集整理的关于决策树知识点的全部内容,更多相关决策树知识点内容请搜索靠谱客的其他文章。








发表评论 取消回复