3. 决策树算法梳理

1. 信息论基础

熵：信息熵是度量样本集合纯度最常用的一种指标。假定当前样本集合D中第k类样本所占的比例为pk,则D的信息熵定义为

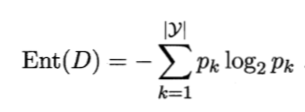
Ent(D)的值越小，则D的纯度越高。

联合熵：度量一个联合分布的随即系统的不确定度

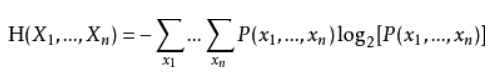
条件熵：表示在已知随机变量X的条件下Y的条件概率分布的熵对X的数学期望

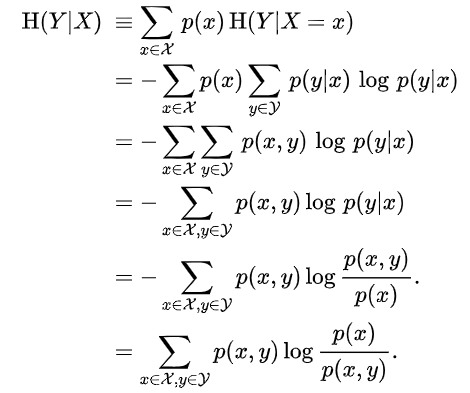
信息增益：某个属性对样本划分的影响程度

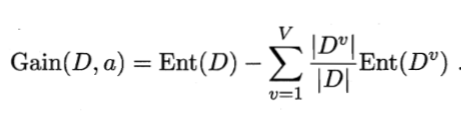
基尼不纯度：来自集合中的某种结果随机应用在集合中，某一数据项的预期误差率

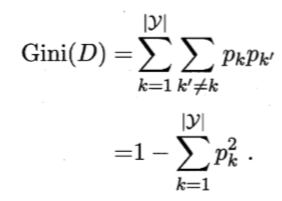
2. 决策树的不同分类算法（ID3算法、C4.5、CART分类树）的原理及应用场景

ID3算法：

核心是在决策树各个节点上根据信息增益来选取属性，逐步向下构建决策树。

具体方法：1）从根节点开始，计算各个属性的信息增益，选择信息增益最大值的属性作为节点的属性。2）利用该属性将结点样本划分到子节点。3）递归构建决策树。4）若属性集为空，则选取数量最多的类别作为叶节点的类别，若样本集为空，则设为父节点中样本最多的类别。

C4.5算法：

基于ID3的改进：1）用信息增益率来选择划分特征。2）在构造树的过程中进行剪枝。3）可对连续值与缺失值进行处理。

CART分类树：

递归地二分每个特征，将输入空间划分为有限个单元

1）计算现有属性的基尼指数

2）在所有可能的属性A及该属性的所有可能取值a中，选择基尼指数最小的样本及其对应的取值作为最优属性和最优切分点，将本节点的数据集二分，生成两个子节点。

3）对两个子节点递归地调用上述步骤，直至节点中的样本个数小于阈值，或者样本集的基尼指数小于阈值，或者没有更多特征后停止。

3. 回归树原理

最小二叉回归树生成算法：在训练数据集所在的输入空间中，递归地将每个区域划分为两个子区域并决定每个子区域上输出值，构建二叉决策树。

1）选择最优切分变量j与切分点s，求解

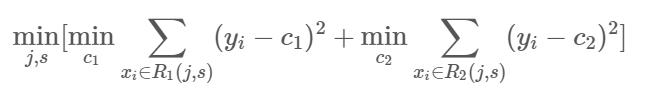
遍历变量j，对固定的切分变量j扫描切分点s，选择使上式最小值的对(j,s)。其中Rm是被划分的输入空间，cm是空间Rm对应的固定输出值。

2）用选定的（j,s)划分区域并决定相应的输出值

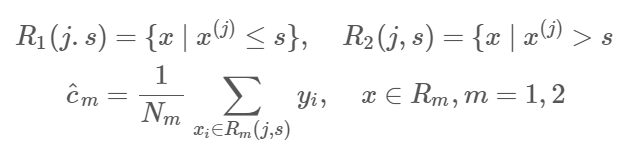
3）重复1）、2）直到满足停止条件，生成决策树。

4. 决策树防止过拟合手段

先剪枝：通过提前停止树的构建而对树“剪枝”，一旦停止，节点就成为树叶。该树叶可以持有子集元组中最频繁的类限制决策树的高度和叶子结点处样本的数目

1. 定义一个高度，当决策树达到该高度时就可以停止决策树的生长，这是一种最为简单的方法；
2. 达到某个结点的实例具有相同的特征向量，即使这些实例不属于同一类，也可以停止决策树的生长。这种方法对于处理数据中的数据冲突问题非常有效；
3. 定义一个阈值，当达到某个结点的实例个数小于该阈值时就可以停止决策树的生长；
4. 定义一个阈值，通过计算每次扩张对系统性能的增益，并比较增益值与该阈值的大小来决定是否停止决策树的生长。

后剪枝：它首先构造完整的决策树，允许树过度拟合训练数据，然后对那些置信度不够的结点子树用叶子结点来代替，该叶子的类标号用该结点子树中最频繁的类标记。后剪枝的剪枝过程是删除一些子树，然后用其叶子节点代替，这个叶子节点所标识的类别通过大多数原则(majority class criterion)确定。所谓大多数原则，是指剪枝过程中, 将一些子树删除而用叶节点代替,这个叶节点所标识的类别用这棵子树中大多数训练样本所属的类别来标识,所标识的类称为majority class .相比于先剪枝，这种方法更常用，正是因为在先剪枝方法中精确地估计何时停止树增长很困难。

1)REP方法是一种比较简单的后剪枝的方法，在该方法中，可用的数据被分成两个样例集合：一个训练集用来形成学习到的决策树，一个分离的验证集用来评估这个决策树在后续数据上的精度，确切地说是用来评估修剪这个决策树的影响。这个方法的动机是：即使学习器可能会被训练集中的随机错误和巧合规律所误导，但验证集合不大可能表现出同样的随机波动。所以验证集可以用来对过度拟合训练集中的虚假特征提供防护检验。

该剪枝方法考虑将书上的每个节点作为修剪的候选对象，决定是否修剪这个结点有如下步骤组成：

1. 删除以此结点为根的子树
2. 使其成为叶子结点
3. 赋予该结点关联的训练数据的最常见分类
4. 当修剪后的树对于验证集合的性能不会比原来的树差时，才真正删除该结点

5. 模型评估

机器学习过程分为原型设计阶段（Prototyping）与应用阶段（Deployed）, 其中有原型设计阶段（Prototyping）的离线评估与应用阶段（Deployed）的在线评估(online evaluation).

Prototyping阶段是使用历史数据训练一个适合解决目标任务的一个或多个机器学习模型，并对模型进行验证（Validation）与离线评估（Offline evaluation），然后通过评估指标选择一个较好的模型。我们上面的例子就是Prototyping.

Deployed阶段是当模型达到设定的指标值时便将模型上线，投入生产，使用新生成的在线数据来对该模型进行在线评估（Online evaluation），在线测试不同于离线测试，有着不同的测试方法以及评价指标。最常见的便是A/B testing，它是一种统计假设检验方法。 离线评估和在线评估采用不同的评估指标,在对模型进行离线评估时是采用偏经验误差的方法,在在线评估时会采用业务指标,如设备使用效率(OEE), 用户点击率等.

6. sklearn参数详解，Python绘制决策树

DecisionTreeClassifier(criterion="gini", splitter="best", max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0., max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0., min_impurity_split=None, class_weight=None, presort=False)

1）criterion:string, optional (default="gini") (1).criterion='gini',分裂节点时评价准则是Gini指数。 (2).criterion='entropy',分裂节点时的评价指标是信息增益。

2）max_depth:int or None, optional (default=None)。指定树的最大深度。 如果为None，表示树的深度不限。直到所有的叶子节点都是纯净的，即叶子节点 中所有的样本点都属于同一个类别。或者每个叶子节点包含的样本数小于min_samples_split。

3）splitter:string, optional (default="best")。指定分裂节点时的策略。 (1).splitter='best',表示选择最优的分裂策略。 (2).splitter='random',表示选择最好的随机切分策略。

4）min_samples_split:int, float, optional (default=2)。表示分裂一个内部节点需要的做少样本数。 (1).如果为整数，则min_samples_split就是最少样本数。 (2).如果为浮点数(0到1之间)，则每次分裂最少样本数为ceil(min_samples_split * n_samples)

5）min_samples_leaf: int, float, optional (default=1)。指定每个叶子节点需要的最少样本数。 (1).如果为整数，则min_samples_split就是最少样本数。 (2).如果为浮点数(0到1之间)，则每个叶子节点最少样本数为ceil(min_samples_leaf * n_samples)

6）min_weight_fraction_leaf:float, optional (default=0.) 指定叶子节点中样本的最小权重。

7）max_features:int, float, string or None, optional (default=None). 搜寻最佳划分的时候考虑的特征数量。 (1).如果为整数，每次分裂只考虑max_features个特征。 (2).如果为浮点数(0到1之间)，每次切分只考虑int(max_features * n_features)个特征。 (3).如果为'auto'或者'sqrt',则每次切分只考虑sqrt(n_features)个特征 (4).如果为'log2',则每次切分只考虑log2(n_features)个特征。 (5).如果为None,则每次切分考虑n_features个特征。 (6).如果已经考虑了max_features个特征，但还是没有找到一个有效的切分，那么还会继续寻找 下一个特征，直到找到一个有效的切分为止。

8）random_state:int, RandomState instance or None, optional (default=None) (1).如果为整数，则它指定了随机数生成器的种子。 (2).如果为RandomState实例，则指定了随机数生成器。 (3).如果为None，则使用默认的随机数生成器。

9）max_leaf_nodes: int or None, optional (default=None)。指定了叶子节点的最大数量。 (1).如果为None,叶子节点数量不限。 (2).如果为整数，则max_depth被忽略。

10）min_impurity_decrease:float, optional (default=0.) 如果节点的分裂导致不纯度的减少(分裂后样本比分裂前更加纯净)大于或等于min_impurity_decrease，则分裂该节点。 加权不纯度的减少量计算公式为： min_impurity_decrease=N_t / N * (impurity - N_t_R / N_t * right_impurity - N_t_L / N_t * left_impurity) 其中N是样本的总数，N_t是当前节点的样本数，N_t_L是分裂后左子节点的样本数， N_t_R是分裂后右子节点的样本数。impurity指当前节点的基尼指数，right_impurity指 分裂后右子节点的基尼指数。left_impurity指分裂后左子节点的基尼指数。

11）min_impurity_split:float 树生长过程中早停止的阈值。如果当前节点的不纯度高于阈值，节点将分裂，否则它是叶子节点。 这个参数已经被弃用。用min_impurity_decrease代替了min_impurity_split。

12）class_weight:dict, list of dicts, "balanced" or None, default=None 类别权重的形式为{class_label: weight} (1).如果没有给出每个类别的权重，则每个类别的权重都为1。 (2).如果class_weight='balanced'，则分类的权重与样本中每个类别出现的频率成反比。 计算公式为：n_samples / (n_classes * np.bincount(y)) (3).如果sample_weight提供了样本权重(由fit方法提供)，则这些权重都会乘以sample_weight。

13）presort:bool, optional (default=False) 指定是否需要提前排序数据从而加速训练中寻找最优切分的过程。设置为True时，对于大数据集 会减慢总体的训练过程；但是对于一个小数据集或者设定了最大深度的情况下，会加速训练过程。

参考：

周志华——机器学习

https://www.cethik.vip/2016/09/21/machineCAST/

最后

以上就是碧蓝金毛为你收集整理的3. 决策树算法梳理的全部内容，希望文章能够帮你解决3. 决策树算法梳理所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。