DFS

思路

题意就是：给你一个非空数组，和为sum，你能否找到一个子序列，和为sum/2。

• 如果sum为奇数，肯定找不到，因为sum/2为小数，而数组只包含正整数。
• 如果sum为偶数，有可能找到。

对于每个元素，都有 选或不选它 去组成子序列。我们可以 DFS 回溯去穷举所有的情况。

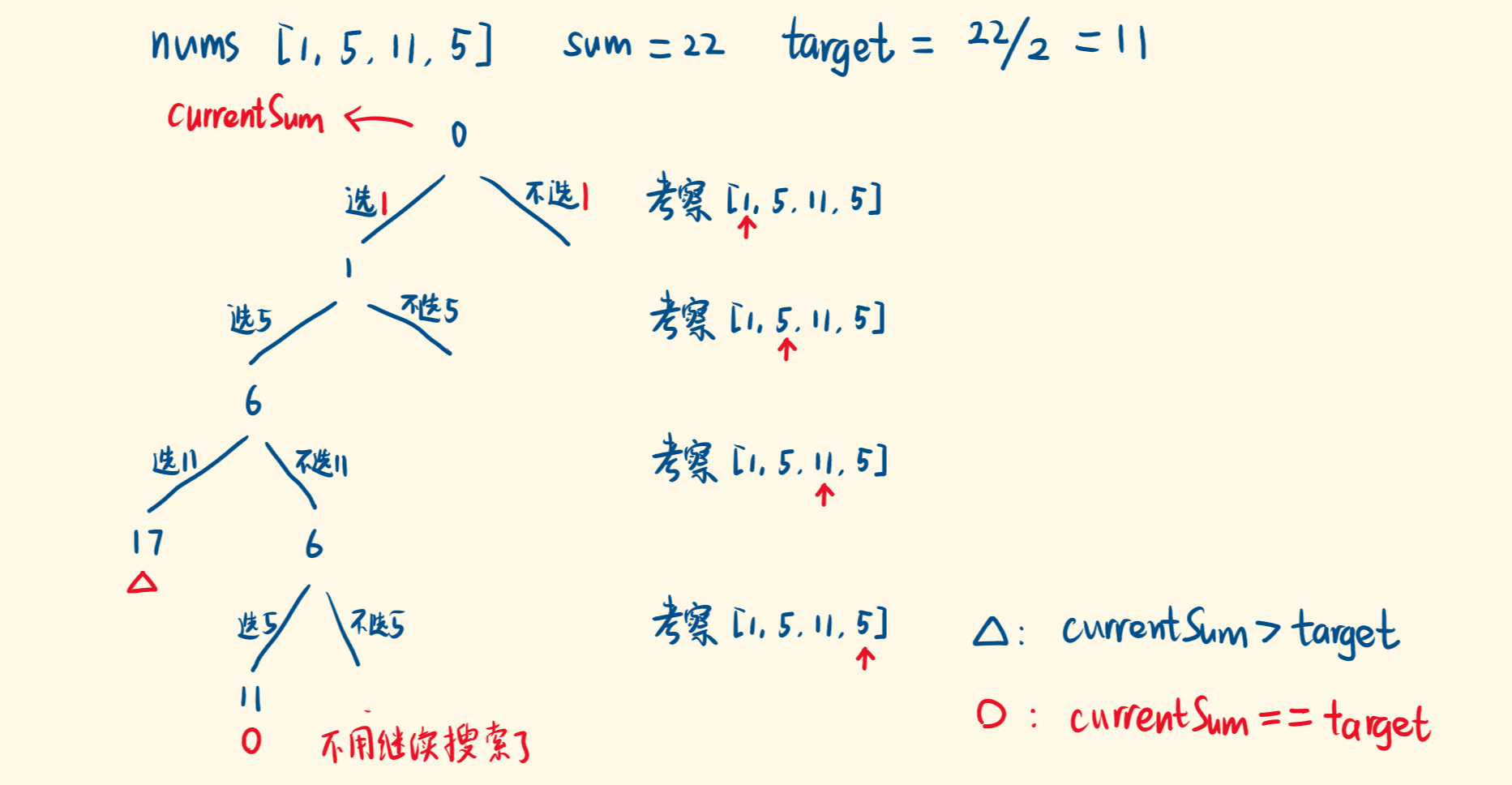
每次考察一个元素，用索引i描述，还有一个状态：当前累加的curSum。
递归函数：基于已选的元素（和为curSum），从i开始继续选，能否选出和为sum/2的子集。
每次递归，都有两个选择：

• 选nums[i]。基于选它，往下继续选（递归）：dfs(curSum + nums[i], i + 1)
• 不选nums[i]。基于不选它，往下继续选（递归）：dfs(curSum, i + 1)

递归的终止条件有三种情况：

• curSum > target，已经爆了，不用继续选数字了，终止递归，返回false。
• curSum == target，满足条件，不用继续选数字了，终止递归，返回true。
• 指针越界，考察完所有元素，能走到这步说明始终没有返回false。

代码:

class Solution {
public:
	bool canPartition(vector<int>& nums) 
	{
		//数组元素个数小于两个，肯定无法分成两个子序列
		if (nums.size() < 2) return false;
		//数组和为奇数，也不满足条件
		int Sum = accumulate(nums.begin(), nums.end(), 0);
		if (Sum%2!=0) return false;
		return dfs(0,0,Sum/2,nums);
	}
	//cursum:当前累加和  i:当前索引  target:目标和
	bool dfs(int cursum,int i,int target, vector<int>& nums)
	{
		if (cursum == target) return true;//找到目标和
		//超和，越界
		if (cursum > target || i >= nums.size()) return false;
			//选择当前数字
			bool sel = dfs(cursum + nums[i], i+1, target, nums);
		//不选择当前数字
			bool unsel = dfs(cursum, i + 1, target, nums);
			return sel || unsel;
	}
};

记忆化搜索

上面递归超时了怎么办，遇事不决，记忆力学
这里用unordered_map容器保存计算出来的结果，防止重复计算

代码：

class Solution {
	unordered_map<string,bool> cache;//缓存器---保存当前索引值对应累加和下的真假
public:
	bool canPartition(vector<int>& nums) 
	{
		//数组元素个数小于两个，肯定无法分成两个子序列
		if (nums.size() < 2) return false;
		//数组和为奇数，也不满足条件
		int Sum = accumulate(nums.begin(), nums.end(), 0);
		if (Sum%2!=0) return false;
		return dfs(0,0,Sum/2,nums);
	}
	//cursum:当前累加和  i:当前索引  target:目标和
	bool dfs(int cursum,int i,int target, vector<int>& nums)
	{
		string key = to_string(i) + '&' + to_string(cursum);
		//当前索引值对应累加和下的真假
		if (cache.find(key) != cache.end()) return cache[key];
		if (cursum == target) return true;//找到目标和
		//超和，越界
		if (cursum > target || i >= nums.size()) return false;
		bool ret=dfs(cursum + nums[i], i+1, target, nums)|| dfs(cursum, i + 1, target, nums);
		return cache[key]= ret;
	}
};

注意：这里用map加pair会超时

class Solution {
	map<pair<int,int>,bool> cache;//缓存器---保存当前索引值对应累加和下的真假
public:
	bool canPartition(vector<int>& nums) 
	{
		//数组元素个数小于两个，肯定无法分成两个子序列
		if (nums.size() < 2) return false;
		//数组和为奇数，也不满足条件
		int Sum = accumulate(nums.begin(), nums.end(), 0);
		if (Sum%2!=0) return false;
		return dfs(0,0,Sum/2,nums);
	}
	//cursum:当前累加和  i:当前索引  target:目标和
	bool dfs(int cursum,int i,int target, vector<int>& nums)
	{
		//当前索引值对应累加和下的真假
		if (cache.find({ i,cursum }) != cache.end()) return cache[{i, cursum}];
		if (cursum == target) return true;//找到目标和
		//超和，越界
		if (cursum > target || i >= nums.size()) return false;
	    //选择当前数字
		bool sel = dfs(cursum + nums[i], i+1, target, nums);
		//不选择当前数字
		bool unsel = dfs(cursum, i + 1, target, nums);
		return cache[{i,cursum}]= (sel || unsel);
	}
};

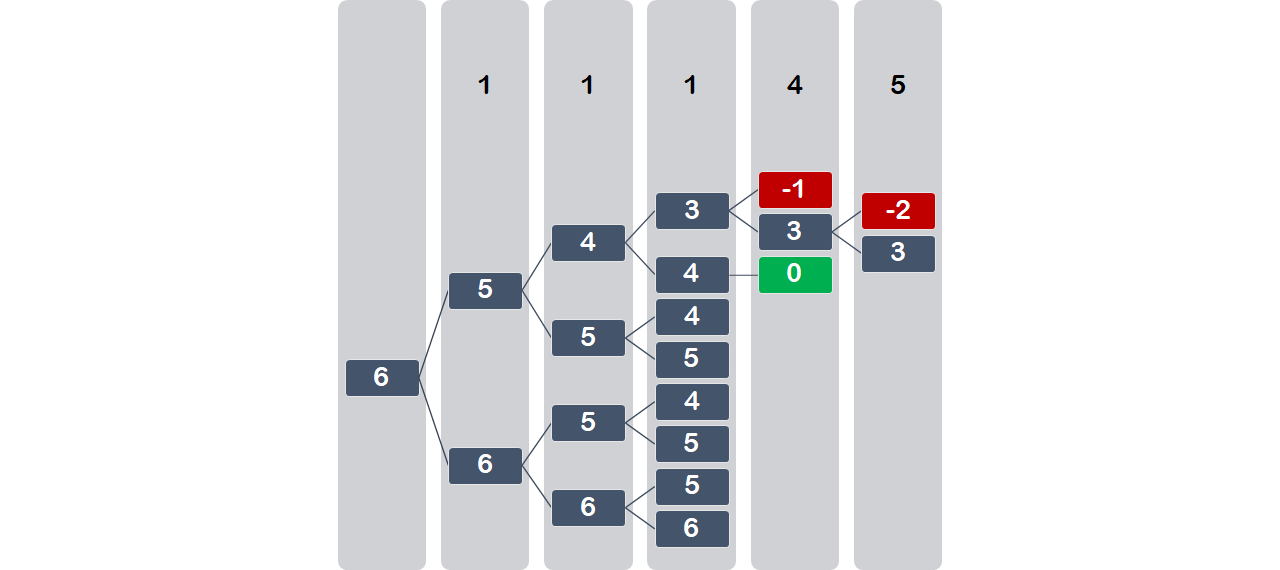
记忆化搜索的另一种写法

这里再对之前重复计算问题用图片配文字解释一下

输入 [1, 1, 1, 4, 5]，总和sum为12，取半half为6；
针对第一个元素，减去得5，不减得6，依次产生完全二叉树；
出现负数直接返回否，等于0直接返回是。

里面有大量重复元素。思考发现，在二叉树的同一层出发，如果剩下的数字remain一样大，它后续的分支是完全相同的。

“只选第一个1”和“只选第二个1”的结果是一样的；
同一层的两个remain如果相同，它们的子树就完全相同。

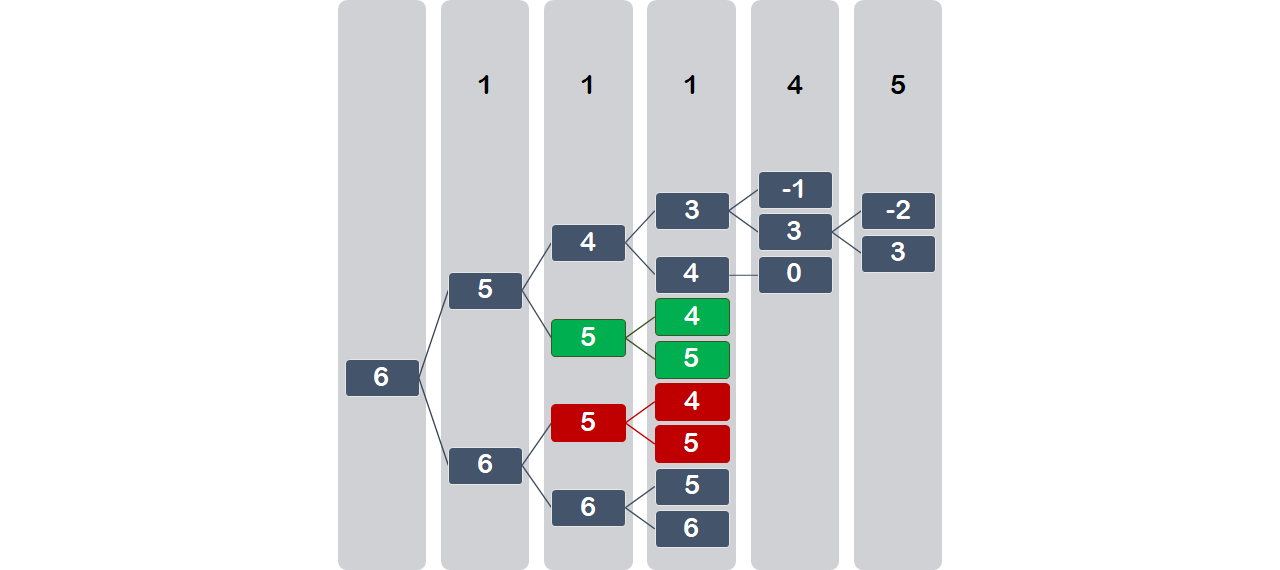
针对这种情况我们引入记忆化搜索。

每次递归，我们检查这个remain是否在这一层出现过。如果是，就跳过这个结点。

代码：

class Solution {
	vector<unordered_set<int>> dp;
public:
	bool canPartition(vector<int>& nums) 
	{
		if (nums.size() < 2) return false;
		int Sum = accumulate(nums.begin(), nums.end(), 0);
		if (Sum%2!=0) return false;
		dp.resize(nums.size());
		return dfs(Sum/2,0,nums);
	}
	bool dfs(int remain,int i,vector<int>& nums)
	{
		if (remain==0) return true;
		if (remain<0|| i == nums.size()|| dp[i].find(remain) != dp[i].end()) return false;
		dp[i].insert(remain);
		return dfs(remain, i + 1, nums)|| dfs(remain - nums[i], i + 1,nums);
	}
};

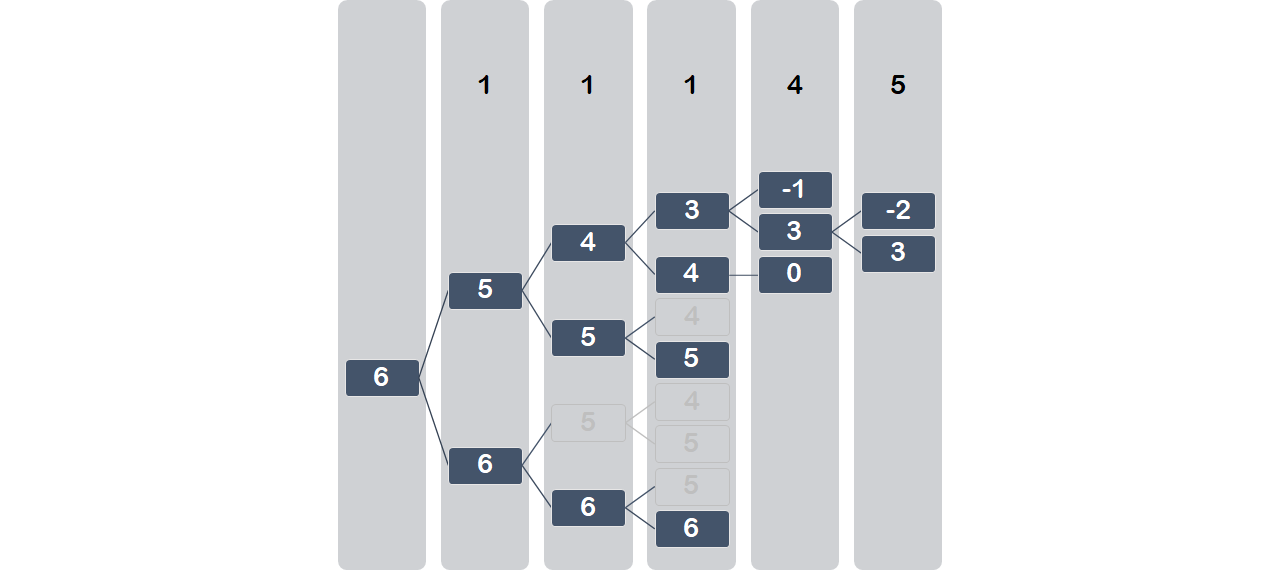
可以看到，现在每一层同一个remain数字只出现一次。

动态规划

基本分析

• 通常「背包问题」相关的题，都是在考察我们的「建模」能力，也就是将问题转换为「背包问题」的能力。
• 由于本题是问我们能否将一个数组分成两个「等和」子集。
• 问题等效于能否从数组中挑选若干个元素，使得元素总和等于所有元素总和的一半。
• 这道题如果抽象成「背包问题」的话，应该是：
• 我们背包容量为 target=sum/2，每个数组元素的「价值」与「成本」都是其数值大小，求我们能否装满背包。

转换为 01 背包
没了解过01背包问题的建议先看这篇文章

• 由于每个数字（数组元素）只能被选一次，而且每个数字选择与否对应了「价值」和「成本」，求解的问题也与「最大价值」相关。
• 可以使用「01 背包」的模型来做。
• 当我们确定一个问题可以转化为「01 背包」之后，就可以直接套用「01 背包」的状态定义进行求解了。
• 注意，我们积累 DP 模型的意义，就是在于我们可以快速得到可靠的「状态定义」。
• 在 路径问题 中我教过你通用的 DP 技巧解法，但那是基于我们完全没见过那样的题型才去用的，而对于一些我们见过题型的 DP题目，我们应该直接套用（或微调）该模型「状态定义」来做。
• 我们直接套用「01 背包」的状态定义：
• f[i][j] 代表考虑前 i个数值，其选择数字总和不超过 j 的最大价值。
• 当有了「状态定义」之后，结合我们的「最后一步分析法」，每个数字都有「选」和「不选」两种选择。
• 因此不难得出状态转移方程：
  
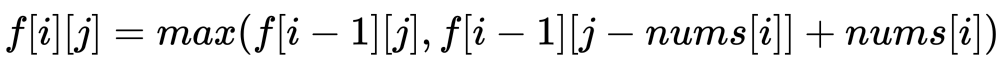
  大白话:把数组总和一半看做背包容量和我们需要找的价值，数组元素同时表示物品大小和物品价值，并且每个物品只能选择一次，现在让你在不超过背包容量的情况下，尽量往背包里面塞入物品，并且价值要尽可能大，最终如果最大价值与要找的价值吻合说明存在解，小于说明不存在解，不存在大于的情况，因为这里物品大小就是物品的价值，背包最大容量就是背包塞入物品的最大价值

代码：

class Solution {
public:
	bool canPartition(vector<int>& nums) 
	{
		if (nums.size() < 2) return false;
		int Sum = accumulate(nums.begin(), nums.end(), 0);
		if (Sum&1) return false;
		//行标:对应每个物品  列表:对应容量  dp[i][j]:当前物品对应当前容量状态下的最大价值
		vector<vector<int>> dp(nums.size(),vector<int>(Sum/2+1));
		//初始化第一行---将第一件物品所有状态进行初始
		for (int i = 0; i <= Sum / 2; i++)//前提是当前对应容量能够塞下第一个物品
			dp[0][i] = i >= nums[0] ? nums[0] : 0;
		//计算其他行
		for (int i = 1; i <nums.size(); i++)
		{
			for (int j = 0; j <= Sum / 2; j++)
			{
				//不选当前物品放入背包
				int unsel = dp[i - 1][j];
				//选当前物品放入背包---先看当前对应容量下能不能塞的下
				int sel = j >= nums[i] ? dp[i - 1][j - nums[i]] + nums[i] :0;

				dp[i][j] = max(sel, unsel);
			}
		}
		// 如果最大价值等于 target，说明可以拆分成两个「等和子集」
		return dp[nums.size()-1][Sum/2] == Sum/2;
	}
};

「滚动数组」解法

在上一讲我们讲到过「01 背包」具有两种空间优化方式。

其中一种优化方式的编码实现十分固定，只需要固定的修改「物品维度」即可。

代码：

class Solution {
public:
	bool canPartition(vector<int>& nums) 
	{
		if (nums.size() < 2) return false;
		int Sum = accumulate(nums.begin(), nums.end(), 0);
		if (Sum&1) return false;
		//行标:对应每个物品  列表:对应容量  dp[i][j]:当前物品对应当前容量状态下的最大价值
		vector<vector<int>> dp(2,vector<int>(Sum/2+1));
		//初始化第一行---将第一件物品所有状态进行初始
		for (int i = 0; i <= Sum / 2; i++)//前提是当前对应容量能够塞下第一个物品
			dp[0][i] = i >= nums[0] ? nums[0] : 0;
		//计算其他行
		for (int i = 1; i <nums.size(); i++)
		{
			for (int j = 0; j <= Sum / 2; j++)
			{
				//不选当前物品放入背包
				int unsel = dp[(i - 1)&1][j];
				//选当前物品放入背包---先看当前对应容量下能不能塞的下
				int sel = j >= nums[i] ? dp[(i - 1)&1][j - nums[i]] + nums[i] :0;

				dp[i&1][j] = max(sel, unsel);
			}
		}
		// 如果最大价值等于 target，说明可以拆分成两个「等和子集」
		return dp[(nums.size()-1)&1][Sum/2] == Sum/2;
	}
};

「一维空间优化」解法

事实上，我们还能继续进行空间优化：只保留代表「剩余容量」的维度，同时将容量遍历方向修改为「从大到小」。
遍历方向从大到小是防止数据覆盖操作，详情可以去看上面给出链接的01背包问题的文章

代码：

class Solution {
public:
	bool canPartition(vector<int>& nums) 
	{
		if (nums.size() < 2) return false;
		int Sum = accumulate(nums.begin(), nums.end(), 0);
		if (Sum&1) return false;
		vector<int> dp(Sum / 2 + 1); // 将「物品维度」取消

		for (int i = 0; i < nums.size(); i++)
		{
			int t = nums[i];//临时记录当前物品的大小
			//从尾往前进行覆盖操作，是因为在计算下一行时会用到前面的数据和对应自身的原始数据，尾端不存在会利用到的数据
			//如果当前容量小于当前要塞入物品大小，那么下面就不用看了，等于当前物品不放入背包，数据等于上一行数据
			for (int j = Sum / 2; j >= nums[i]; j--)
			{
				//不选当前物品
				int us = dp[j];
				//选当前物品
				int s = j >= t ? t + dp[j - t] : 0;

				dp[j] = max(us, s);
			}
		}
		return dp[Sum / 2]==Sum/2;
	}
};

最后

以上就是碧蓝金毛为你收集整理的leetcode 416. 分割等和子集DFS记忆化搜索记忆化搜索的另一种写法动态规划「滚动数组」解法「一维空间优化」解法的全部内容，希望文章能够帮你解决leetcode 416. 分割等和子集DFS记忆化搜索记忆化搜索的另一种写法动态规划「滚动数组」解法「一维空间优化」解法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。