matlab雅可比迭代法解线性方程组_大规模对称正定稀疏线性方程组的求解与代数多重网格...

问题定义

很多问题都可以抽象为求解下列优化的问题：

往往对于实际应用时，可能还会加入一些正则项，最终表示为求解优化：

这个问题有一个解析解：

因此上述问题等于求解线性方程组:

对于图像问题，一方面由于绝大多数模型都只会建立某个像素与它局部之间的关系，因此线性方程组的系数矩阵

通常满足某种特定的稀疏性；另一方面，由于图像分辨率较高，因此线性方程组维度实际上极大，导致快速计算难度较大。 因此，这个问题的最终核心在于：

迭代法的阵亡

对于简单迭代法，如雅可比迭代，高斯-塞德尔迭代等，都存在高频快速收敛，低频难以收敛的问题。 简单来说，对于柏松问题：

这个问题在某种程度上等价于求解柏松方程

离散化之后的线性方程组对应每一行的方程为(一维情况):

对于上述问题使用雅可比松弛迭代(假设松弛变量为

)，得到迭代矩阵的特征值和特征向量分别为(

为向量维度,

):

其中

表示第i个网格点的坐标 由此，可以发现，对于这个问题，

设置为1，那么频率越高,k越大，

越接近于0，收敛越快。 因此对于这类问题，往往高频的收敛性更好，低频收敛性更差。

几何多重网格

为了解决低频收敛慢的问题，多重网格算法应运而生。 核心思想在于，在细网格上的低频可以变为粗网格上的高频。 注意到对于

，如果N变为N/2实际上可以认为频率变为了原来的两倍，那么收敛性自然会变好。 因此，我们可以先在细网格上迭代，消除了高频误差，然后放到粗网格迭代，消除细网格上的低频误差，然后再在粗网格上refine最终结果，大致流程如下图：

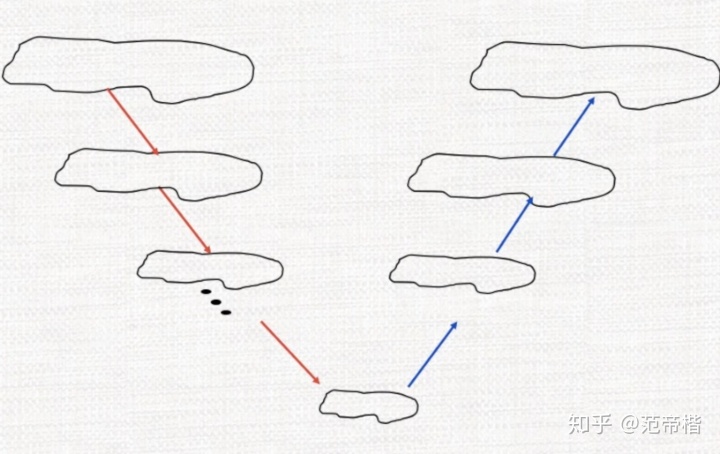
这个方法实际上是比较简单的，网格如下所示：

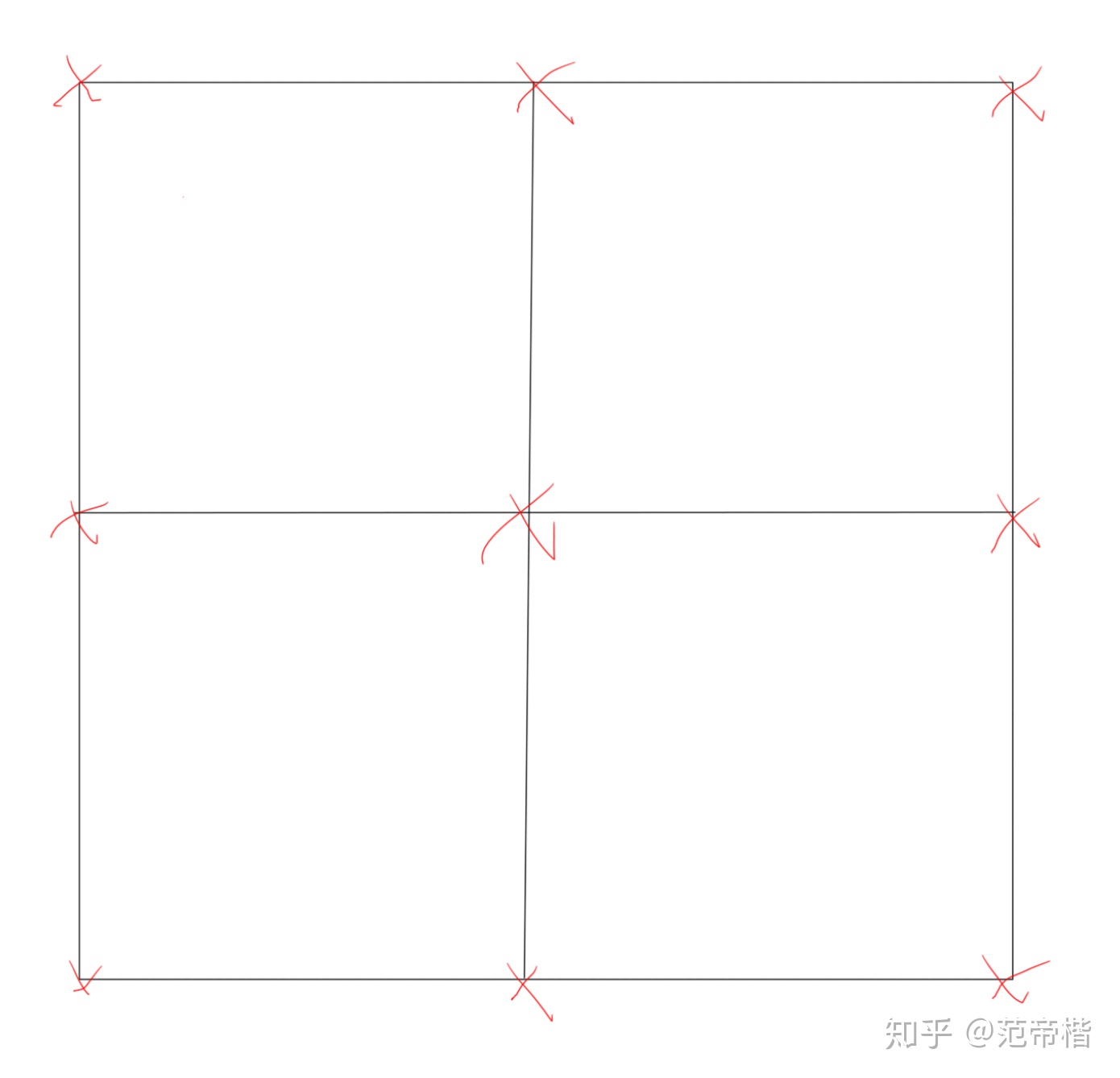
红色的点代表粗网格上的节点，如果我们将网格细化，那么，可以得到细网格的点：

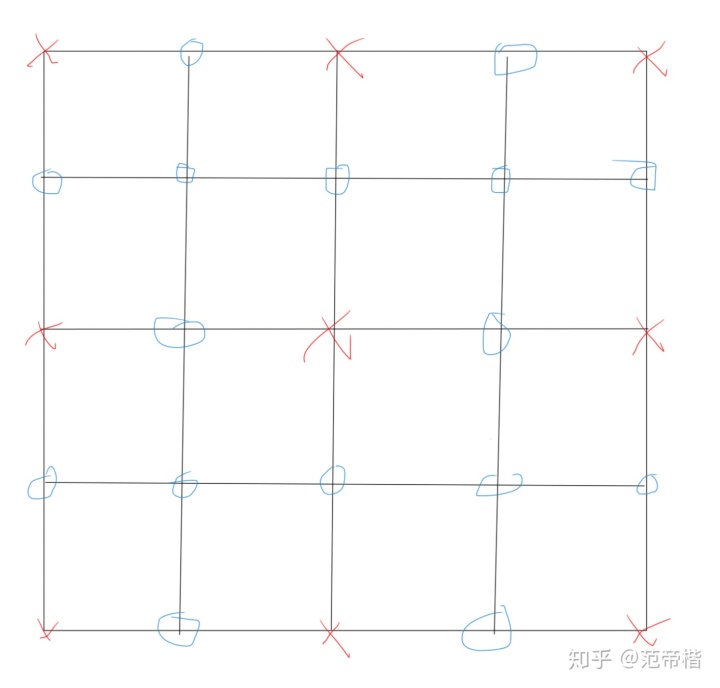
这些点的值通过粗网格插值而来，也就是说，几何多重网格实际上是依赖于实际的网格，人为设定了粗网格和细网格，从而设置的一种多重网格算法。

注意到这种方法细网格上的节点上一定有粗网格上的节点，因此原来如果粗细网格原来是同一个点，只需要将粗网格上的点赋值到细网格上，如果是新的点，那么需要对它进行插值，假设这个矩阵为

，

之后插值即可。

但实际上这样做是不对的。回到最初的问题，我们要消除的是低频误差，也就是“光滑”误差，

在粗网格上迭代后的结果实际上和光滑没有太多关系，我们迭代后的结果，实际上是

其中

那么，我们的误差方程应该如何建立呢？

定义残差:

由此，我们有误差方程：

由于我们希望将低频误差放到粗网格上进行消除，因此我们实际上将

最终，我们实际上计算了：

，然后插值得到

，最后补偿到

上。

代数多重网格

是否有一种方法可以依赖于系数矩阵本身的特性，从而设计一种多重网格方法，与实际网格无关，从而得到更好的收敛性呢？实际上是有的，这个方法就是代数多重网格。 由于我们现在没有了实际网格，那么实际上为了使用多重网格技术，我们需要回答两个问题：

1. 要选择哪些节点为粗网格上的节点
2. 如何插值

对于问题1，实际上我们是需要准从两个原则：得到的粗网格节点能够通过插值表示细网格节点，或者说粗网格节点一定原来有和细网格节点相连。另一方面，我们希望粗节点能够尽量少，从而求解线性方程组的规模可以更小。 对于这个问题有个经典方法: 即Ruge提出来的方法

对于问题2，回答了两个子问题： 1) 插值公式长什么样 2)粗网格上的线性方程组长什么样

通常如果插值矩阵为

，那么粗网格上的线性方程组的系数矩阵构建为:

因此实际上核心还是在于如何插值。

假设

表示连接i和j节点的边的权重，同时我们认为残差几乎为0，由此可以得到:

由此:

由于这些边连接的节点可以分为3类：

• 细网格上的节点
• 粗网格上的节点
• 连接极弱的节点

若用C表示粗节点误差集合，F表示细节点误差集合，W表示弱连接集合，可以将求和部分分为三块：

由于弱连接集合的连接已经足够弱，因此我们强制认为这部分的

,由此可以得到新的近似公式：

对于粗网格上的$e_j$实际上在粗网格上已经算出，而细网格上的

实际上是没有的。 对于这部分有连接的细网格上的

，我们找到和它相连的所有粗网格的节点

，通过公式：

对它进行近似计算。