我想提出另一种基于网格搜索的解决方案。 它不如Ander先进,也不如rahnema1短,但是它应该很容易理解和理解。 而且,它运行非常快。
该算法包括几个阶段:
我们生成一个均匀间隔的网格。
我们找到网格中点到所有提供的点的最小距离。
我们会丢弃所有距离低于某个百分位数(例如第95个百分点)的点。
我们选择包含最大距离的区域(如果我的初始网格足够精细,则该区域应包含正确的中心)。
我们围绕所选区域创建一个新的网格并再次找到距离(这部分显然不是最优的,因为距离是计算到所有点的,包括远点和无关点)。
我们迭代区域内的细化,同时关注值的前5%的方差->如果它下降到某个预设阈值以下,我们将中断。
几点注意事项:
我已经做出了这样的假设:圆不能超出分散点的范围(即散布的边界正方形充当“看不见的墙”)。
适当的百分位数取决于初始网格的精细程度。 这也将影响[x,y,r] = [0.7832, 2.0694, 0.7815]的迭代次数,以及cnt的最佳初始值。
function [xBest,yBest,R] = q42806059
rng(1)
x=rand(1,100)*5;
y=rand(1,100)*5;
%% Find the approximate region(s) where there exists a point farthest from all the rest:
xExtent = linspace(min(x),max(x),numel(x));
yExtent = linspace(min(y),max(y),numel(y)).';
% Create a grid:
[XX,YY] = meshgrid(xExtent,yExtent);
% Compute pairwise distance from grid points to free points:
D = reshape(min(pdist2([XX(:),YY(:)],[x(:),y(:)]),[],2),size(XX));
% Intermediate plot:
% figure(); plot(x,y,'.k'); hold on; contour(XX,YY,D); axis square; grid on;
% Remove irrelevant candidates:
D(D
D(D > xExtent | D > yExtent | D > yExtent(end)-yExtent | D > xExtent(end)-xExtent) = NaN;
%% Keep only the region with the largest distance
L = bwlabel(~isnan(D));
[~,I] = max(table2array(regionprops('table',L,D,'MaxIntensity')));
D(L~=I) = NaN;
% surf(XX,YY,D,'EdgeColor','interp','FaceColor','interp');
%% Iterate until sufficient precision:
xExtent = xExtent(~isnan(min(D,[],1,'omitnan')));
yExtent = yExtent(~isnan(min(D,[],2,'omitnan')));
cnt = 1; % increase or decrease according to the nature of the problem
while true
% Same ideas as above, so no explanations:
xExtent = linspace(xExtent(1),xExtent(end),20);
yExtent = linspace(yExtent(1),yExtent(end),20).';
[XX,YY] = meshgrid(xExtent,yExtent);
D = reshape(min(pdist2([XX(:),YY(:)],[x(:),y(:)]),[],2),size(XX));
D(D
I = find(D == max(D(:)));
xBest = XX(I);
yBest = YY(I);
if nanvar(D(:)) < 1E-10 || cnt == 10
R = D(I);
break
end
xExtent = (1+[-1 +1]*10^-cnt)*xBest;
yExtent = (1+[-1 +1]*10^-cnt)*yBest;
cnt = cnt+1;
end
% Finally:
% rectangle('Position',[xBest-R,yBest-R,2*R,2*R],'Curvature',[1 1],'EdgeColor','r');
我从Ander的示例数据中得到的结果是[x,y,r] = [0.7832, 2.0694, 0.7815](相同)。 执行时间大约是Ander解决方案的一半。
以下是中间图:
从一个点到所有提供的点集的最大(清晰)距离的轮廓:
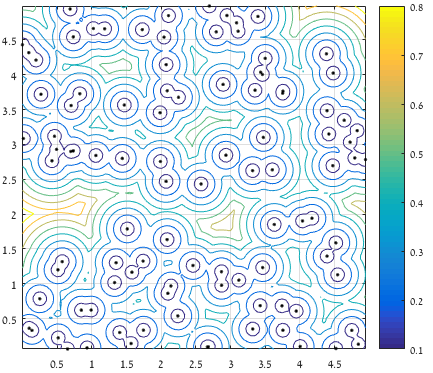
在考虑到边界的距离之后,仅保留最远5%的遥远点,并仅考虑包含最大距离的区域(一块表面代表保留的值):
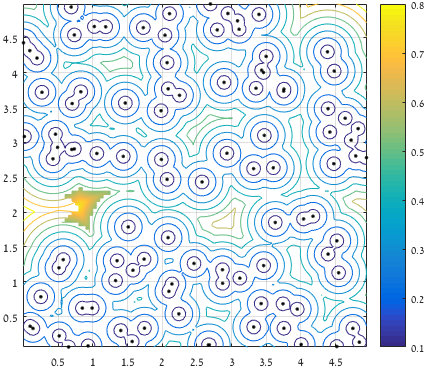
最后:
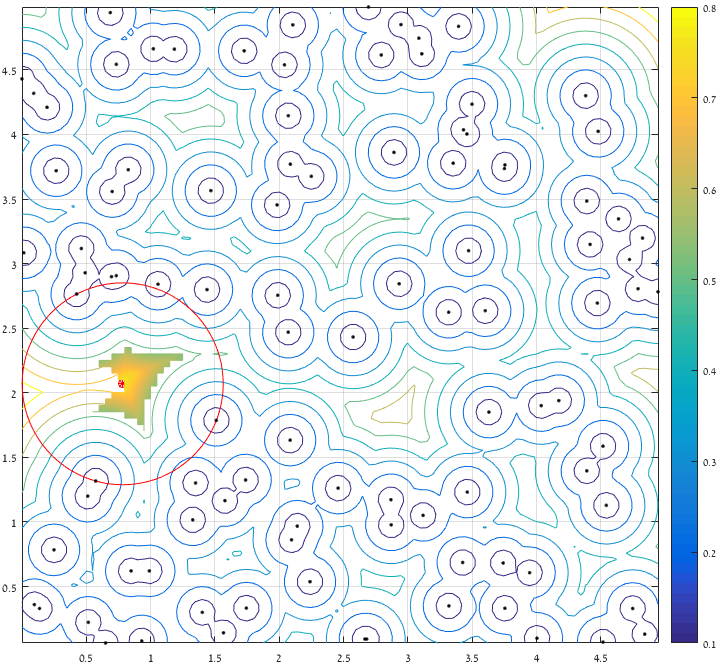
最后
以上就是轻松导师最近收集整理的关于matlab分区域拟合,Matlab-在具有分布parti的图像的自由区域中拟合最大圆的全部内容,更多相关matlab分区域拟合,Matlab-在具有分布parti内容请搜索靠谱客的其他文章。








发表评论 取消回复