文章目录
- 1.计数器
- 1.1 同步计数器
- 1.1.1 同步二进制计数器(介绍74161,74LS191)
- 1.1.2 同步十进制计数器(介绍74160,74LS190)
- 1.2异步计数器
- 2. 关于计数器的组合和转化
- 【问题】:将N进制的计数器转化为M进制的计数器
- (1)当N > M时:
- 当N < M时:
- 2. 时序逻辑电路的设计步骤分析:
1.计数器
1.1 同步计数器
同步计数器的意义:当时钟脉冲输入时触发器的翻转是同时发生的
我们来分析一个同步二进制叫法计数器,理解原理的同时顺便复习一下我们对时序逻辑电路的分析:
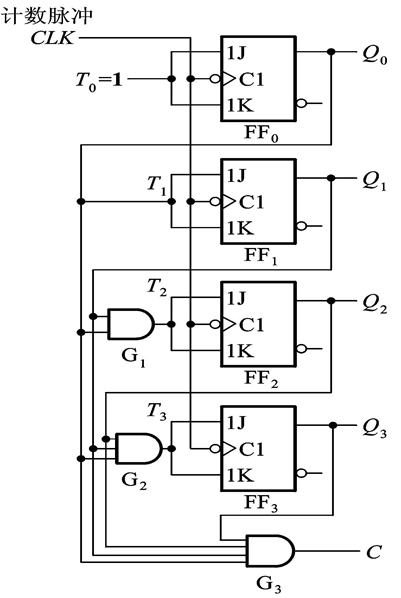
【第一步】写成触发器输入量的逻辑函数式:
{
J
1
=
K
1
=
T
0
=
1
J
2
=
K
2
=
T
1
=
Q
0
J
3
=
K
3
=
T
2
=
Q
1
Q
0
J
4
=
K
4
=
T
3
=
Q
2
Q
1
Q
0
left { begin{array}{c} J_1 = K_1 = T_0 = 1\ J_2 = K_2 = T_1 = Q_0\ J_3=K_3=T_2=Q_1Q_0\ J_4=K_4=T_3=Q_2Q_1Q_0\ end{array} right.
⎩⎪⎪⎨⎪⎪⎧J1=K1=T0=1J2=K2=T1=Q0J3=K3=T2=Q1Q0J4=K4=T3=Q2Q1Q0
【第二步】将触发器的这些输入带入触发器的特性方程
我们知道,JK触发器的特性方程为:
Q
∗
=
J
Q
′
+
K
′
Q
Q^* = JQ'+K'Q
Q∗=JQ′+K′Q,带入,得:
{
Q
0
∗
=
Q
0
′
Q
1
∗
=
Q
0
Q
1
′
+
Q
0
′
Q
1
Q
2
∗
=
Q
1
Q
0
Q
2
′
+
(
Q
1
Q
0
)
′
Q
2
Q
3
∗
=
Q
2
Q
1
Q
0
Q
3
′
+
(
Q
2
Q
1
Q
0
)
′
Q
3
left { begin{array}{c} Q_0^* = Q_0'\ Q_1^*=Q_0Q_1'+Q_0'Q_1\ Q_2^*=Q_1Q_0Q_2'+(Q_1Q_0)'Q_2\ Q_3^*=Q_2Q_1Q_0Q_3'+(Q_2Q_1Q_0)'Q_3\ end{array} right.
⎩⎪⎪⎨⎪⎪⎧Q0∗=Q0′Q1∗=Q0Q1′+Q0′Q1Q2∗=Q1Q0Q2′+(Q1Q0)′Q2Q3∗=Q2Q1Q0Q3′+(Q2Q1Q0)′Q3
【第三步】写输出方程:
C
=
Q
0
Q
1
Q
2
Q
3
C = Q_0Q_1Q_2Q_3
C=Q0Q1Q2Q3
下面,我们来写一下电路的状态转换表:
| Q 0 Q_0 Q0 | Q 1 Q_1 Q1 | Q 2 Q_2 Q2 | Q 3 Q_3 Q3 | Q 0 ∗ Q_0^* Q0∗ | Q 1 ∗ Q_1^* Q1∗ | Q 2 ∗ Q_2^* Q2∗ | Q 3 ∗ Q_3^* Q3∗ | C |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
画出它的状态转换图:
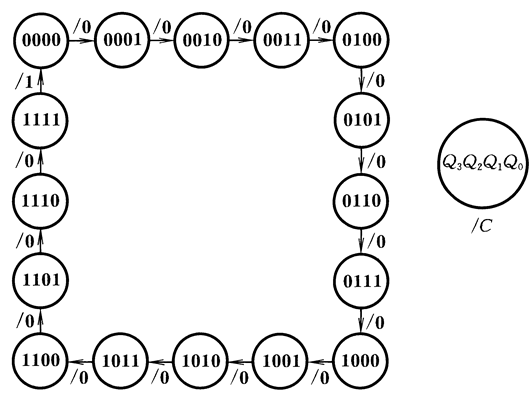
我们发现,每次输入16个计数脉冲,计数器就工作一个循环(工作完一个循环,计数器的进位端C就输出一个1),因此这种计数器也叫做十六进制计数器
画出它的时序图:
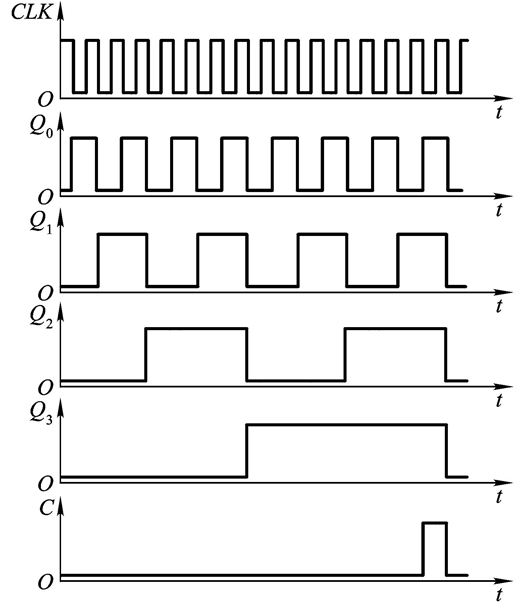
我们发现,输出信号的 Q 0 , Q 1 , Q 2 , Q 3 Q_0,Q_1, Q_2, Q_3 Q0,Q1,Q2,Q3的频率分别为 1 2 C L K , 1 4 C L K , 1 8 C L K , 1 16 C L K frac{1}{2}CLK, frac{1}{4}CLK,frac{1}{8}CLK, frac{1}{16}CLK 21CLK,41CLK,81CLK,161CLK说明这种计数器还具有分频功能
1.1.1 同步二进制计数器(介绍74161,74LS191)
74161
74161的逻辑功能和上面例子中一样,只不过74161还加入了置零和置位的控制信号和置位信号输入端D
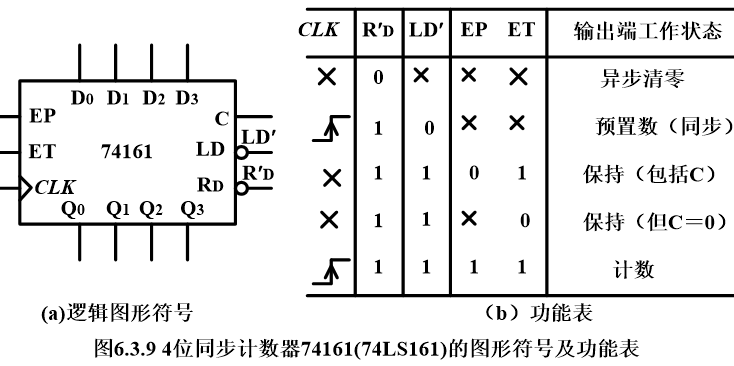
【各个引脚的作用】:
D
0
D_0
D0~
D
3
D_3
D3表示置位输入(也就是当LD’ = 0时将Q置成D所设置好的信号) C:计数的进位输出;
Q
0
Q_0
Q0~
Q
3
Q_3
Q3:计数的输出
【正常计数的条件】:令EP和ET = 1
【预置数和置零】:74161为异步清零(只要
R
D
′
R_D'
RD′=0,触发器就被立刻清零),同步预置数
74161也叫做十六进制计数器
74LS191
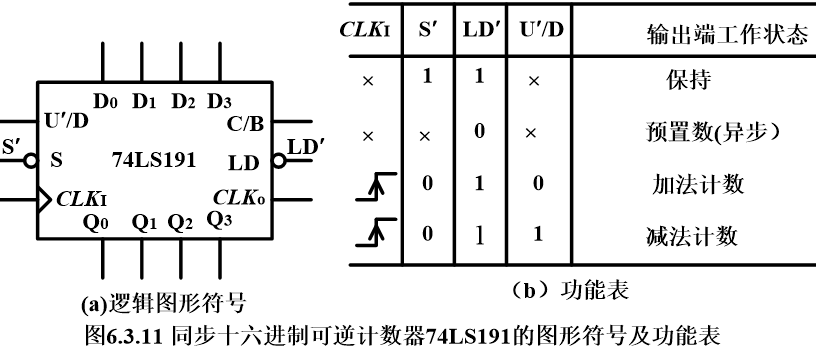
【各个引脚的功能】:同样地,
D
0
D_0
D0~
D
3
D_3
D3是置位信号输入端,
Q
0
Q_0
Q0~
Q
3
Q_3
Q3为计数输出;LD’依然为预置数端口,
U
′
/
D
U'/D
U′/D表示选用加法计数(输出随着CLK在一个工作周期内累加)还是减法计数(输出随CLK在一个工作周期内递减);C/B表示进位/借位输出端
【正常计数的条件】:S’=0
也就是说:74161和74160都是异步清零,同步预置数的;而74LS191和74LS190都是异步清零,异步预置数的
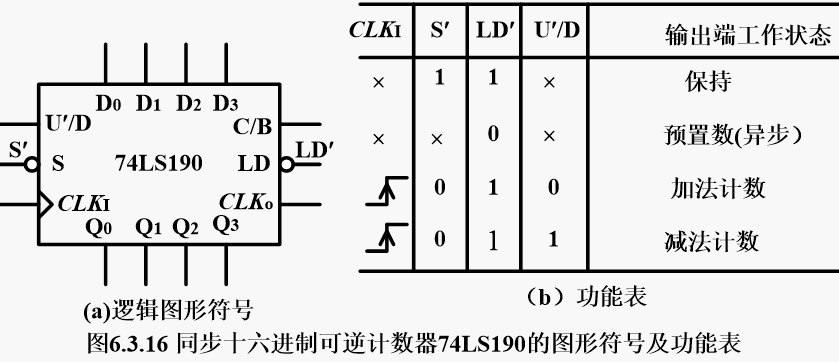
1.1.2 同步十进制计数器(介绍74160,74LS190)
74160
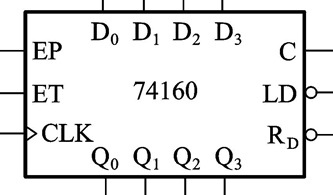
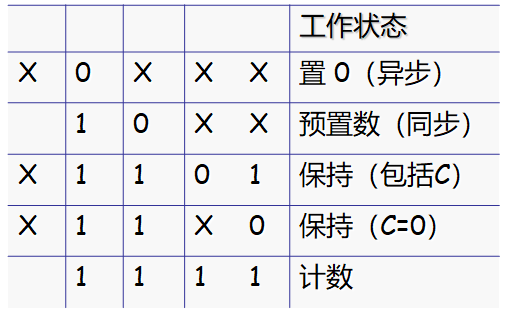
【各个引脚的功能】:LD’为置位端,
D
0
D_0
D0 ~
D
3
D_3
D3为置位信号输入端;
R
D
R_D
RD为置零端,C为进位信号输出,
Q
0
Q_0
Q0~
Q
3
Q_3
Q3为计数输出端
【正常计数的要求】:应该让EP和ET为1
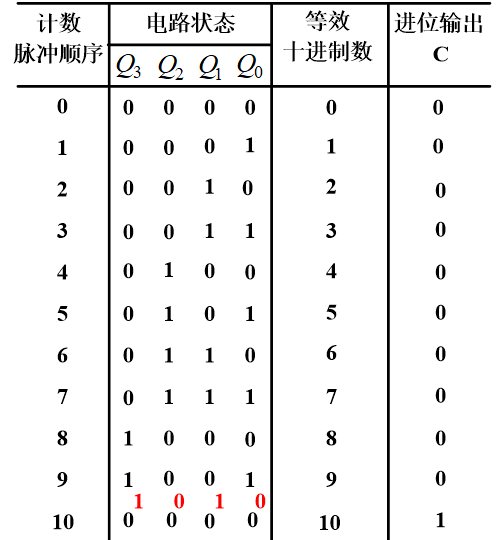
十个CLK信号为一个工作循环,因此是十进制计数器
【状态转换图】:
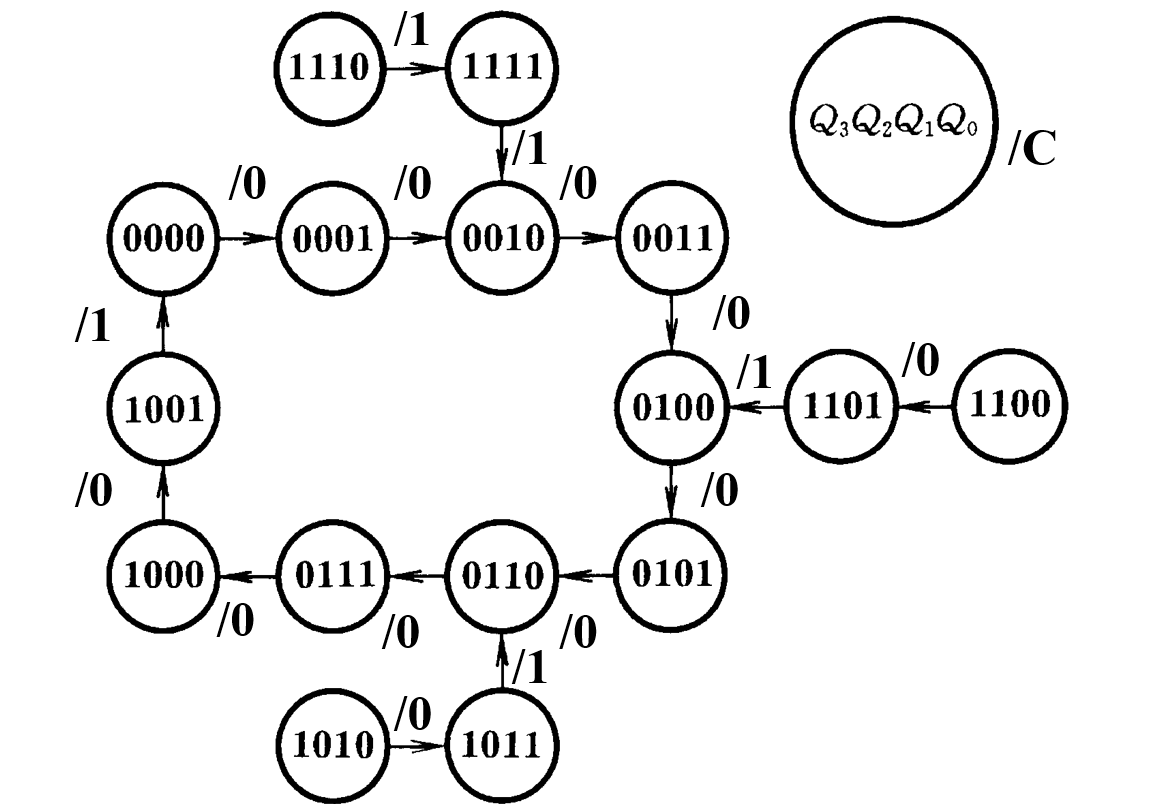
电路可以自启动!
74190
1.2异步计数器
2. 关于计数器的组合和转化
【问题】:将N进制的计数器转化为M进制的计数器
(1)当N > M时:
这时我们采用置零法或者置数法,下面是置零法和置数法的过程图:
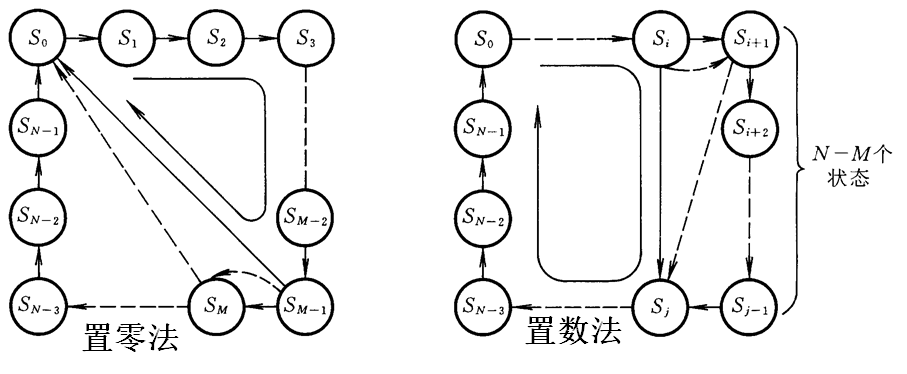
首先记录一下置零法的应用:首先,在我们上面提到的有置零功能的芯片中,置零端都是异步的,也就是说,当我们给了电路这个置零信号之和,电路的状态就会被立刻清零,我们看看上面的左图,这是一个N进制计数器,如果我们想通过置零法将十六进制计数器变成M进制计数器,那么我们就应该在
S
M
S_M
SM处,也就是第M个信号处给出置零信号,那么当
S
M
S_M
SM收到置零信号之后,立刻回到了
S
0
S_0
S0也就是0000处。那么我们计算转换之后的进制数呢,就是从
S
0
S_0
S0记到
S
M
−
1
S_{M-1}
SM−1
那么,要想置零,我们就把需要置零的位置的每一个输出Q,都变成1,然后共同经过一个与非门,在连入RD’,比如下面这个情况:
我们通过Q能看出来,它是想在输出为0110,也就是6时置零,由于74160是异步清零,因此真正要算入循环的就是 S 6 − 1 = S 5 S_{6-1} = S_5 S6−1=S5,那么最终的进制数就是从0到5一共6位,就是六进制
下面再来看看置数法,而置数,就得分同步置数还是异步置数了:比如我们上面介绍的74LS190和74LS191为异步置数;而74160和74161为同步预置数;
注意:我们上图的置数法示意图描述的是异步预置数
和置零法有类似之处:如果为异步预置数,那么如果想从N进制变到M进制,那么我们得从
S
M
+
1
S_{M+1}
SM+1开始置数,但如果是同步预置数,那么我们就从
S
M
S_M
SM开始置数;另外,置零法必须会有0000状态,而置数法是可以从任意状态到任意状态的
【举例】比如说用74161置数法构成七进制计数器:
接法有好多种,我这里只举出两个情况,分别是置数置回到0000和置数置回到另外一个数的
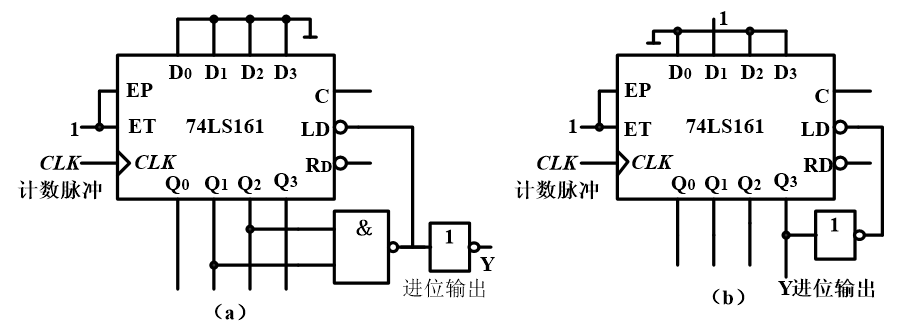
分析一下图(b),我们知道当输出Q为1000也即是8的时候,启动同步置数(记得74160和74161都是同步置数的!)功能,置回什么数呢?这就得看我们得D是啥:0010,也即是2。从8回到2,有:2,3,4,5,6,7,8七位,因此是七进制计数器
当N < M时:
这时,我们就可能需要多片计数器,把他们连接起来使用了。我们在这里主要介绍串行进位和并行进位两种方式。
【串行进位】:以低位芯片的进位输出作为高位芯片的CLK输入,芯片们总时处于计数状态
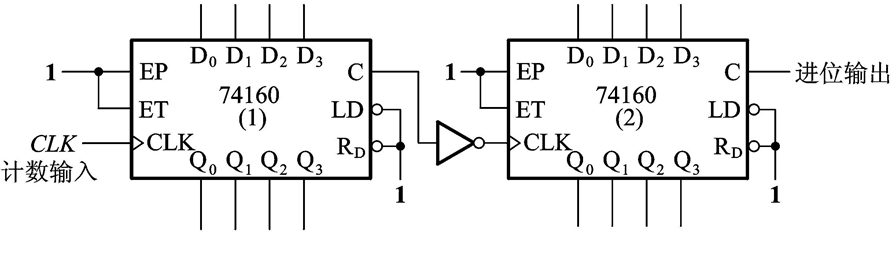
【并行进位】:以低位芯片的进位输出信号作为高位芯片的状态控制信号,同时,所有芯片公用一个CLK信号。(记住:并行连接的话我们所有芯片的CLK都是共用一个的,而把低位芯片的进位输出作为高位芯片的控制信号EP,ET)
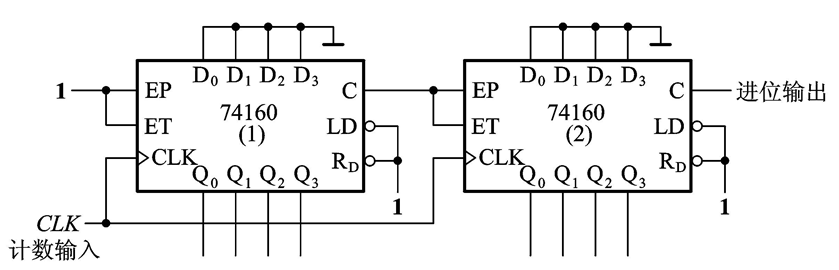
在掌握了上面两种连接方式之和,我们就来看看要转化成的N进制计数器的N取值的情况了:
- 首先,我们看M能不能因式分解,如果M可以分解为:M = N 1 N_1 N1 x N 2 N_2 N2的形式,那么我们就把这两片芯片先分别由N进制接成 N 1 N_1 N1进制和 N 2 N_2 N2进制,然后再通过串行连接或者并行连接组合起来
我发现在使用置数法的时候,我看课本上很喜欢用进位输出C的反向作为LD’的控制信号
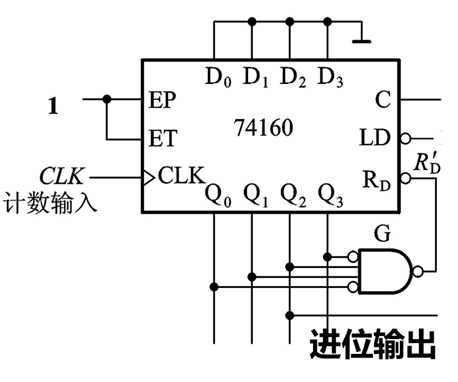
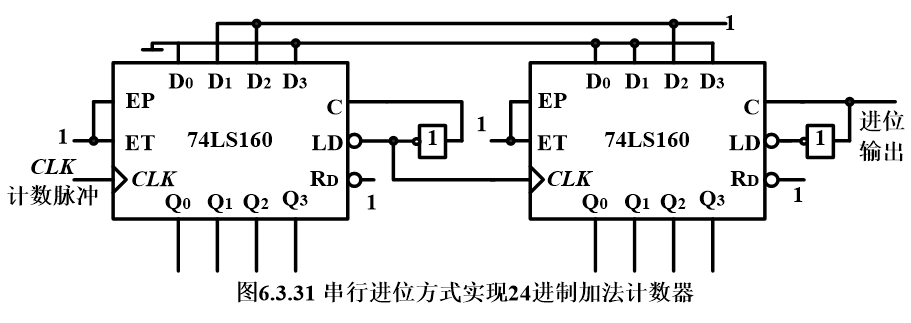
【例子】:要求我们用74160(十进制计数器)构成24进制计数器
方法多样,由于24=4x6=3x8,我们就以4x6为例好了,首先看看串行怎么连接:(记住:串行连接的话就以低位芯片进位输出的反变量作为高位芯片的CLK输入)
对于置数的话,我们就按照课本上大多数习题的处理方法,把进位输出的反变量作为LD’吧:如下
- 但是,当N不能分解的时候怎么办呢??这时,我们采用整体置零法或者整体置数法,也即是我们先把已有的N进制芯片通过串行连接或者并行连接,连接成NxN > M的大芯片,然后对整体才采用置零法或者置数法,置成M进制
用一个例子分析:将十进制计数器接成29进制计数器:
【第一步】由于29不能分解,那么我们就将两个十进制计数器并行连接的方法接成100进制计数器:
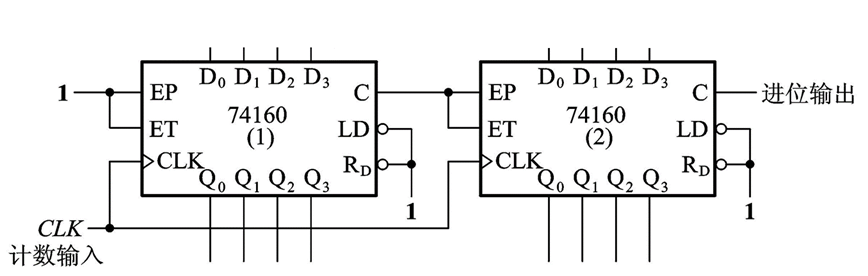
【第二步】开始整体置零,由于74160是异步置零,为了从100进制接到29进制,我们就应该在总计数记到29的时候给出异步置零信号:而总的计数是怎么计算的呢?比如上图,如果芯片(1)的Q输出是1001,也即是9;而芯片(2)的输出是0010,也即是2,那么总的计数就等于:2 x 10 + 9 = 29.
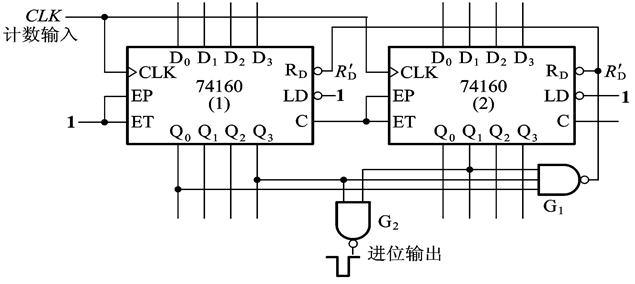
OK,那么,我们就当芯片(1)的Q输出为1001,芯片(2)的输出为0010时给出两个芯片的 R D ′ R_D' RD′置零信号,如下图:
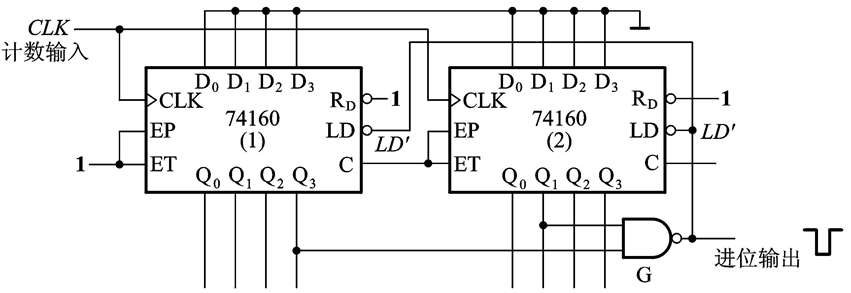
而我们再看看置数是怎么接的,其实也很简单了,但是由于74160是同步预置数,为了简单起见,我们就置数为0好了,那么我们就应该在计数为28的时候给出同步预置数信号LD’:
2. 时序逻辑电路的设计步骤分析:
我们先以用触发器设计M进制计数器为例:(因为这也是考试常考内容)
- 确定需要使用的触发器的个数n:如果我们设计的是M进制计数器,那么电路就会有M个状态,我们有下面的关系式:
2
n
−
1
<
M
<
2
n
2^{n-1} < M < 2^n
2n−1<M<2n
通过这个式子,我们就可以确定所需要的触发器的个数n。 - 写出状态转换表(就是那个Q和 Q ∗ Q^* Q∗关系的表)
- 根据我们写的状态转换表写出 Q ∗ Q^* Q∗的逻辑函数式。
- 把这个 Q ∗ Q^* Q∗的逻辑函数式凑成型如触发器特性方程形式的式子
- 进而得出触发器的输入的逻辑函数式,如果是JK触发器的话,就是得出J = 、、、;K = 、、、
- 得到了触发器的输入,那么就可以开始接线了
【另外:如果我们在用卡诺图对 Q ∗ Q^* Q∗进行化简的时候,把所有的无关项都包进去了,那么最终得到的电路是可以自启动的】
好啦!关于时序逻辑电路里面计数器的笔记终于整理完了哈哈,下面博主就先准备期中考试了
最后
以上就是生动眼睛最近收集整理的关于【数字电子技术 Digital Electronic Technology 7】——时序逻辑电路分析 之 计数器完全攻略1.计数器2. 关于计数器的组合和转化2. 时序逻辑电路的设计步骤分析:的全部内容,更多相关【数字电子技术内容请搜索靠谱客的其他文章。








发表评论 取消回复