MATLAB图像处理学习——高通滤波（频域滤波（二））

目录

1.概论

高通滤波原理

作用

2.理想高通滤波

3.巴特沃斯高通滤波器

代码（巴特沃斯高通滤波器）

4.高斯高通滤波器

1.概论

高通滤波原理：

衰减或抑制低频分量，让高频分量通过

作用：

使图像得到锐化处理，突出图像的边界。

（注意：一般来说，高通滤波对噪声没有任何抑制作用，若简单的使用高通滤波，图像质量可能由于噪声严重而难以达到满意的改善效果，为了既加强图像的细节又抑制噪声，可采用高频加强滤波，这种滤波其实是由一个高通滤波器和一个全通滤波器构成的，这样便能在高通滤波的基础之上保留低频信息）

2.理想高通滤波

产生公式：

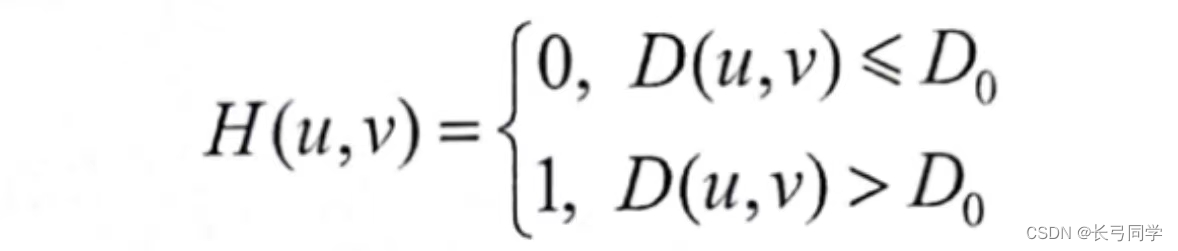
 （其中D0为理想高通滤波器的截止频率）

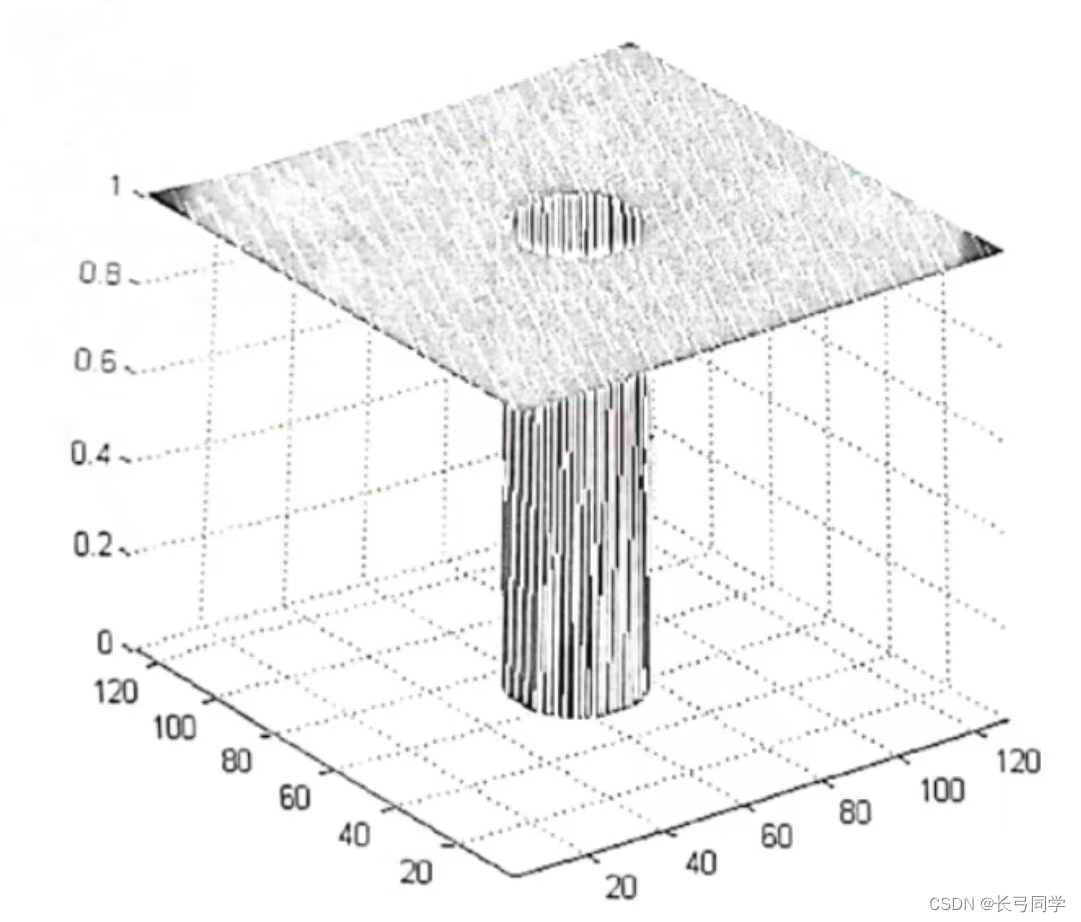
3.巴特沃斯高通滤波器

产生公式：

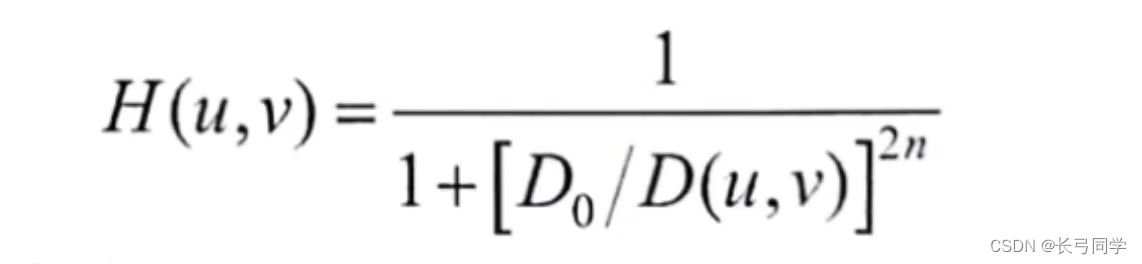
 （其中D0为巴特沃斯高通滤波器的截止频率，n为巴特沃斯滤波器的阶数，用来控制滤波器的陡峭程度）

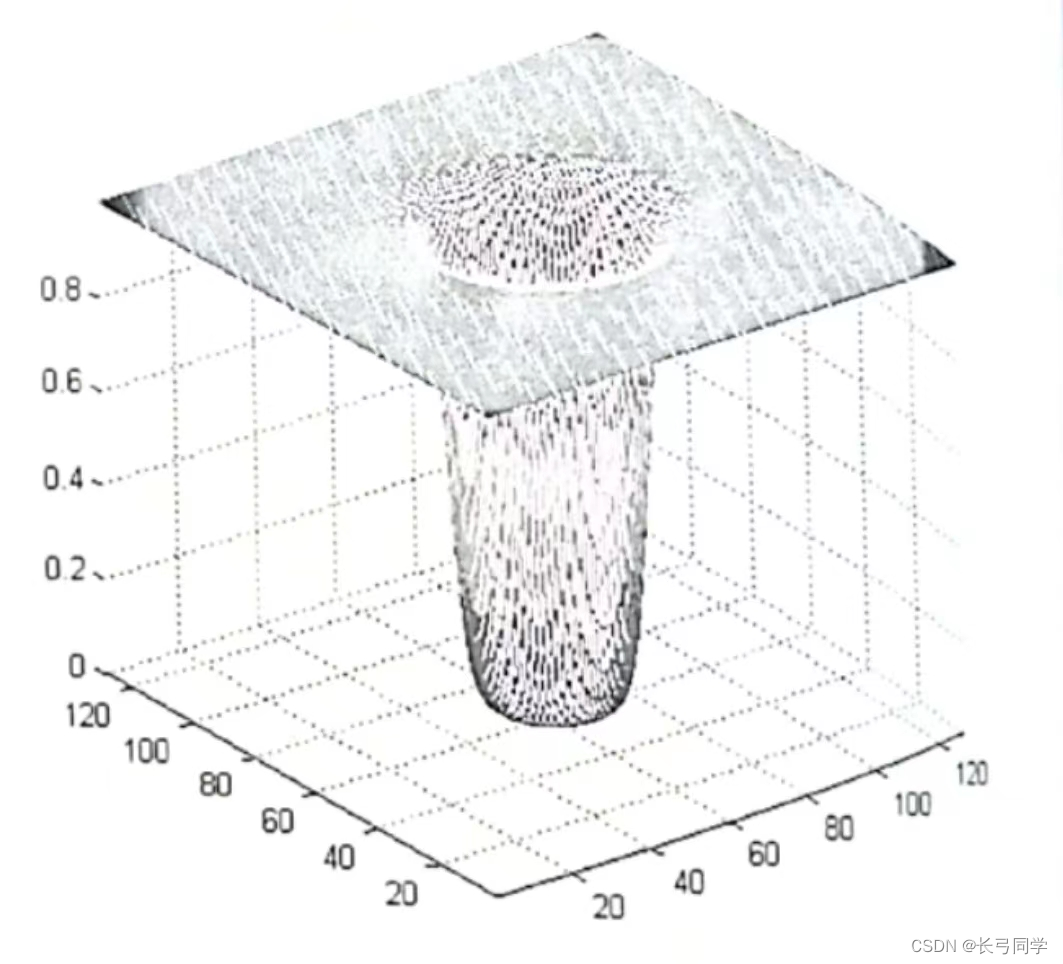
代码（巴特沃斯高通滤波器）：

clear all;clc;
I = imread('D:resource_photo1(1).png');

figure(1);
subplot(221),imshow(I);
title('原始图像');

k=fft2(im2double(I));
s=fftshift(fft2(im2double(I)));

subplot(222),imshow(k);
title('二维傅里叶变换后图像');
subplot(223),imshow(log(abs(s)));
title('中心频谱图像')

[a,b]=size(s);
a0=round(a/2);
b0=round(b/2);
d0=50; % 将理想高通滤波器的截止频率D0设置为50
for i=1:a %双重for循环计算频率点(i,j)与频域中心的距离D(i,j)=sqrt((i-round(a/2)^2+(j-round(b/2)^2))
    for j=1:b 
        distance=sqrt((i-a0)^2+(j-b0)^2);
        if distance<=d0  % 根据理想高通滤波器产生公式,当D(i,j)<=D0,置为0
            h=0;
        else
            h=1;        % 根据理想高通滤波器产生公式,当D(i,j)>D0,置为1
        end
        s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
    end
end
% real函数取元素的实部
s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(224),imshow(s,[]);
title('理想高通滤波所得图像');

 运行结果：

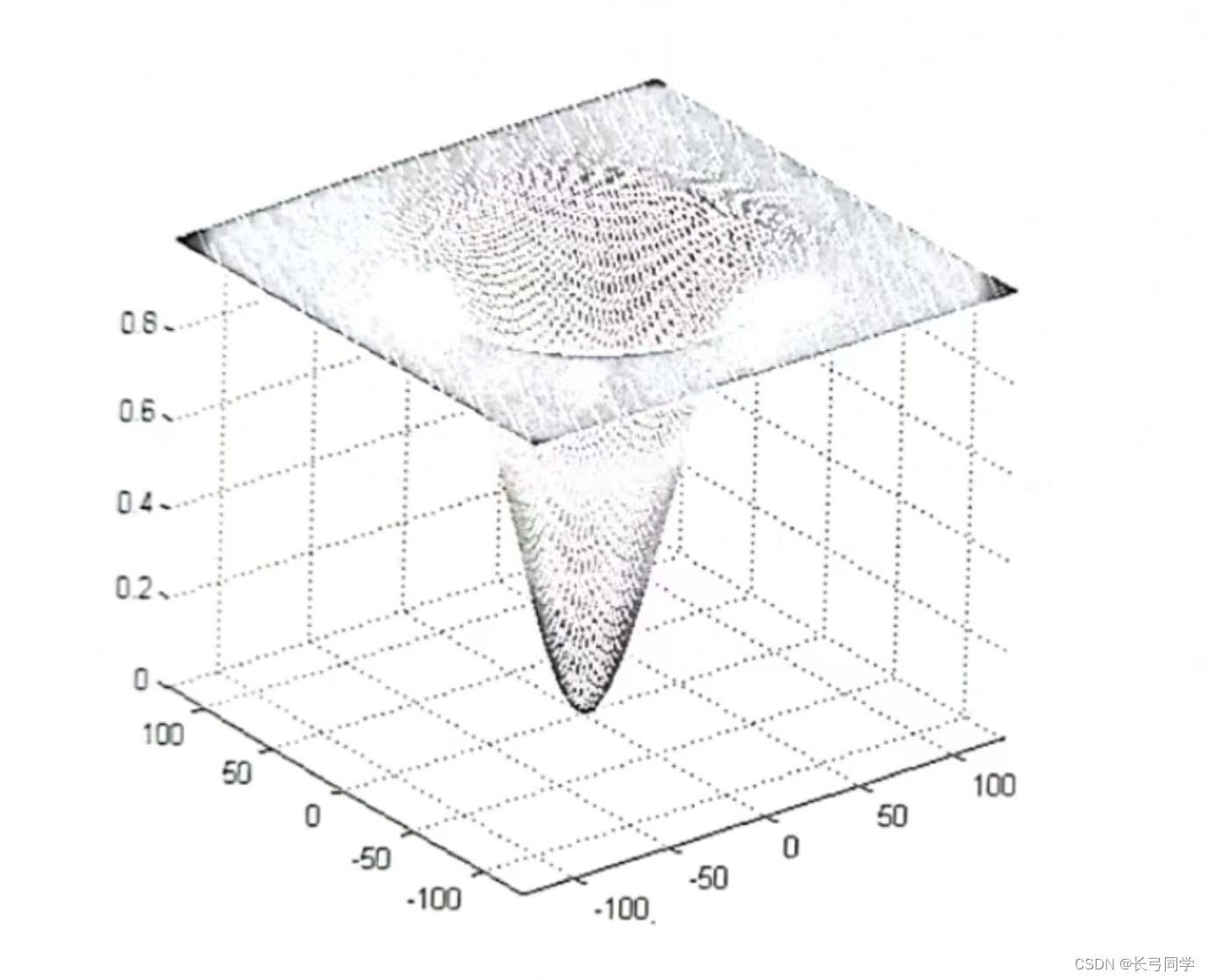
4.高斯高通滤波器

产生公式：

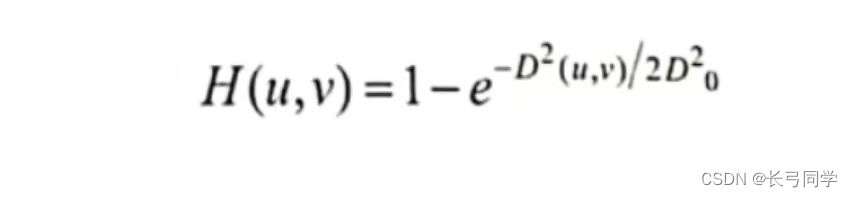
 （其中D0为高斯高通滤波器的截止频率）

最后

以上就是笨笨溪流为你收集整理的MATLAB图像处理学习——高通滤波（频域滤波（二））的全部内容，希望文章能够帮你解决MATLAB图像处理学习——高通滤波（频域滤波（二））所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。