概述
一、在频率域中直接生成滤波器
1，创建用于实现频域滤波器的网格数组的M函数
要在频域内生成一个滤波器，创建一个能够计算任何一点到频率矩形中指定点的距离的M函数是基础的一步。
M函数代码如下：
function [U,V]=dftuv(M,N)
u=single(0:(M-1));
v=single(0:(N-1));
idx=find(u>M/2);
u(idx)=u(idx)-M;
idy=find(v>N/2);
v(idy)=v(idy)-N;
[V,U]=meshgrid(v,u);
dftuv函数能够得到一个网格数组,利用网格数组能够得到任何一点到频率矩形中指定点的距离。
[U,V]=dftuv(8,5);
>> DSQ=U.^2+V.^2
DSQ =
8×5 single 矩阵
0 1 4 4 1
1 2 5 5 2
4 5 8 8 5
9 10 13 13 10
16 17 20 20 17
9 10 13 13 10
4 5 8 8 5
1 2 5 5 2
>> fftshift(DSQ)
ans =
8×5 single 矩阵
20 17 16 17 20
13 10 9 10 13
8 5 4 5 8
5 2 1 2 5
4 1 0 1 4
5 2 1 2 5
8 5 4 5 8
13 10 9 10 13
将 DSQ的ans进行dftshift后得到的就是各点相对频域中心点的距离的平方。
2，低通频域滤波器
理想低通滤波器（ILPF）的传递函数：
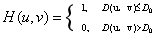
其中D0是正数，D(u,v)是点（u,v）到滤波器中心的距离。该滤波器乘以一幅图像的傅里叶变换，显然滤波器会切断以D0为半径的圆的圆外F(u,v)分量，圆内以及圆上保持不变。但是事实上电子元件无法实现理想的低通滤波器。
常用的有，巴特沃斯低通滤波器，高斯低通滤波器等。
n阶巴特沃斯低通滤波器（BLPF）的传递函数是：
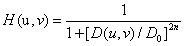
在滤波器中心D0有截止频率，与理想滤波器的区别在于在D0出没有一个尖锐的不连接点。
高斯滤波器（GLPF）的传递函数:
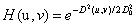
定义M函数生成低通滤波器的传递函数。
function H=lpfilter(type,M,N,D0,n)
[u,v]=dftuv(M,N);
D=hypot(U,V);
switch type
case 'ideal'
H=single(D<=D0);
case 'btw'
if nargin==4
n=1;
end
H=1./(1+(D./D0).^(2*n));
case 'gaussian'
H=exp(-(D.^2)./(2*(D0^2)));
otherwise
error('unkonw filter type.')
end
运用理想低通滤波器对图像进行滤波：
>> f=imread('C:/experiment/test8.jpg');
>> [f,revertclass]=tofloat(f);
>> PQ=paddedsize(size(f));
>> D0=0.05*PQ(2);
>> H=lpfilter('ideal',PQ(1),PQ(2),D0);
>> mesh(H(1:10:540,1:10:800))
>> axis tight
>> F=fft2(f,PQ(1),PQ(2));
>> g=dftfilt(f,H);
>> g=revertclass(g);
>> figure,imshow(fftshift(H))
>> figure,imshow(log(1+abs(fftshift(F))),[])
>> figure,imshow(g)
平滑类图像：
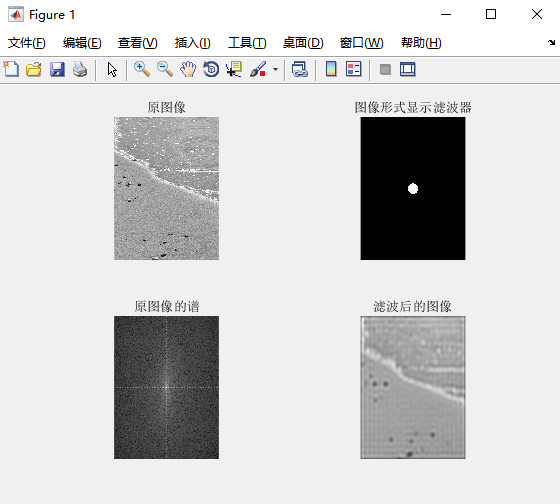
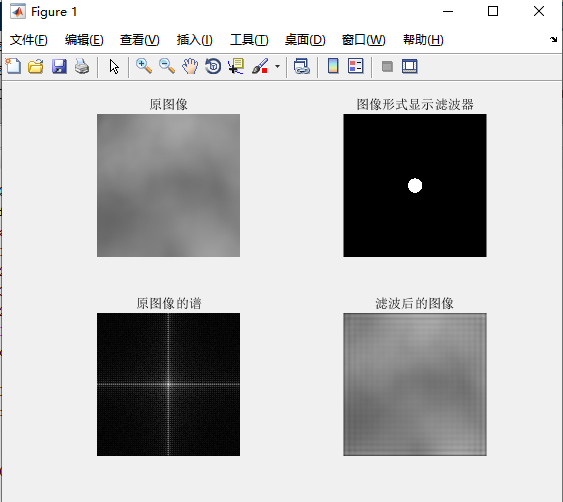
三幅原始图像各自有着不同的特点，第一幅风景图像边缘明显，第二幅沙滩图像沙滩与水面处边界明显，第三幅图想边界模糊。对三幅图像使用理想低通滤波器进行处理，三幅图像与原始图像相比都有些模糊。第一幅图象图像内容的边缘较多，图像边缘全部被模糊，而且由于选择的是理想低通滤波器，可以清楚地看到“振铃效应”。第二幅图像经过滤波后，图像水面与沙滩的边界细节也都被模糊，也存在着”振铃效应“。第三幅图像的原始图像边界模糊，经过理想低通滤波器之后，模糊程度不大，但是依然存在振铃效应。
因为存在“振铃效应”，争对这一点，再次对三幅图像进行处理，选择使用高斯滤波器。
clear all
>> f=imread('C:/experiment/test10.jpg');
f=rgb2gray(f);
[f,revertclass]=tofloat(f);
PQ=paddedsize(size(f));
D0=0.05*PQ(2);
H=lpfilter('gaussian',PQ(1),PQ(2),D0);
mesh(H(1:10:500,1:10:500))
axis tight
F=fft2(f,PQ(1),PQ(2));
g=dftfilt(f,H);
g=revertclass(g);
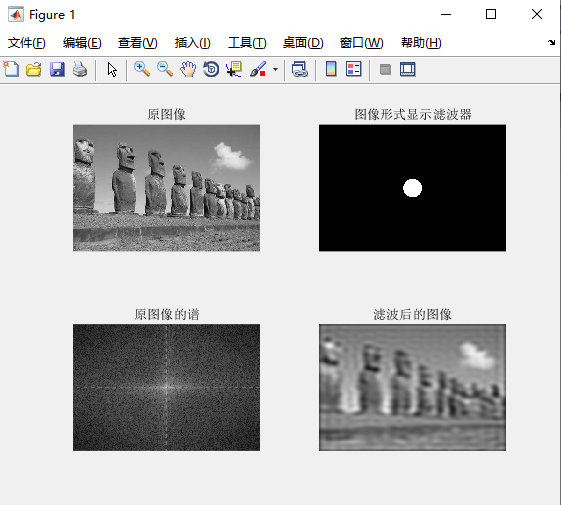
subplot(221),imshow(f),title('原图像');
subplot(222),imshow(fftshift(H)),title('图像形式显示滤波器');
subplot(223),imshow(log(1+abs(fftshift(F))),[]),title('原图像的谱');
subplot(224),imshow(g),title('滤波后的图像');
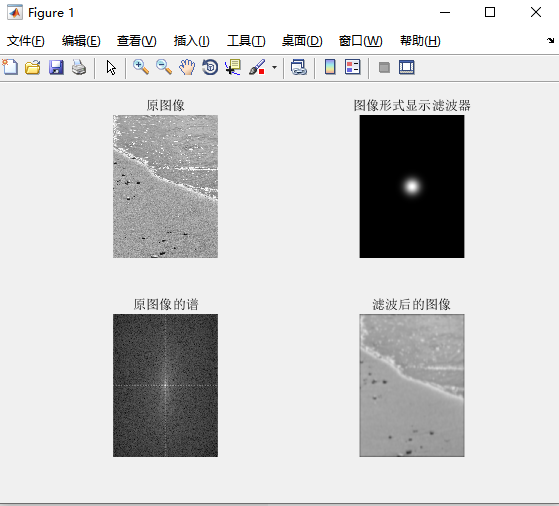
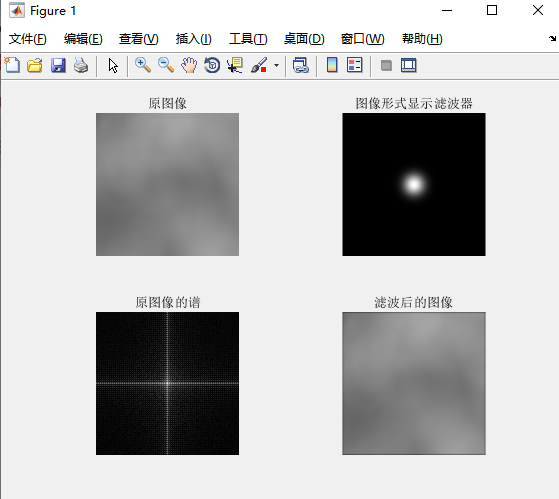
使用高斯低通滤波器，沙滩与水面的边界依旧被模糊，水面以及沙滩上的边缘细节也被模糊，与理想低通滤波器滤波之后的效果类似，区别在于 ，经过高斯低通滤波器处理过后，“振铃效应”消失了。第二幅原始图像边缘细节模糊，经过低通滤波器处理过后，与原图像差别相对与其他两幅图像来说不大，理想滤波器滤波的“振铃效应”也消失了。
显然，低通滤波器使高频分量被滤除，抑制变化快的信号（锯齿，边缘），能够起到平滑图像的作用。当使用理想低通滤波存在振铃效应和折叠误差。
二、高通频域滤波器
与低通频域滤波器模糊图像那样，高通滤波使其相反过程，会锐化图像，原理是抑制低频，保持高频。若给定的低频滤波器的传递函数H(u,v),则，相应高通滤波器的传递函数是1-H(u,v)。
利用这一特性可以写出生成高通频域滤波器的M函数：
function H=hpfilter(type,M,N,D0,n)
if nargin==4
n=1;
end
Hlp=lpfilter(type,M,N,D0,n);
H=1-Hlp;
理想高通滤波器的透视图和图像
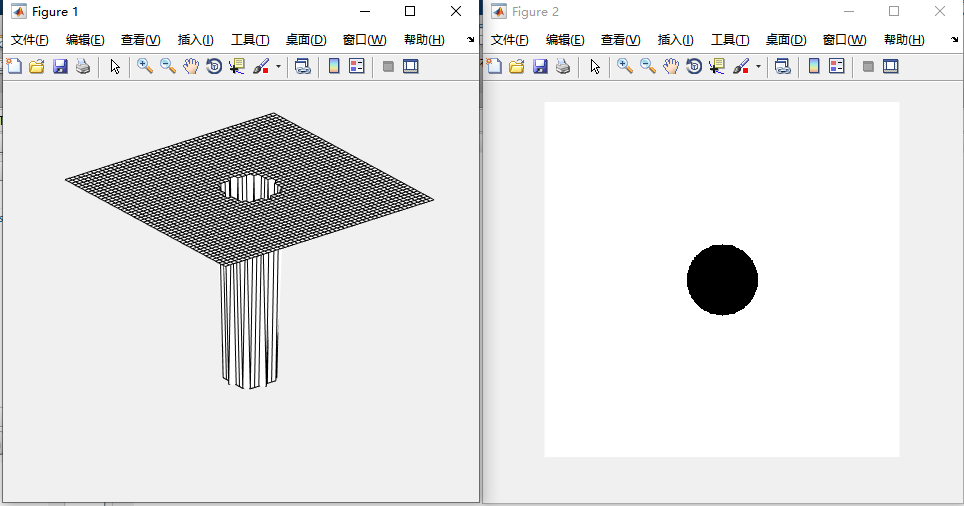
对上面三幅图像使用高通滤波器处理
f=imread('C:/experiment/test9.jpg');
>> f=rgb2gray(f);
>> PQ=paddedsize(size(f));
>> D0=0.05*PQ(1);
>> H=hpfilter('ideal',PQ(1),PQ(2),D0);
>> g=dftfilt(f,H);
>> figure,imshow(g)
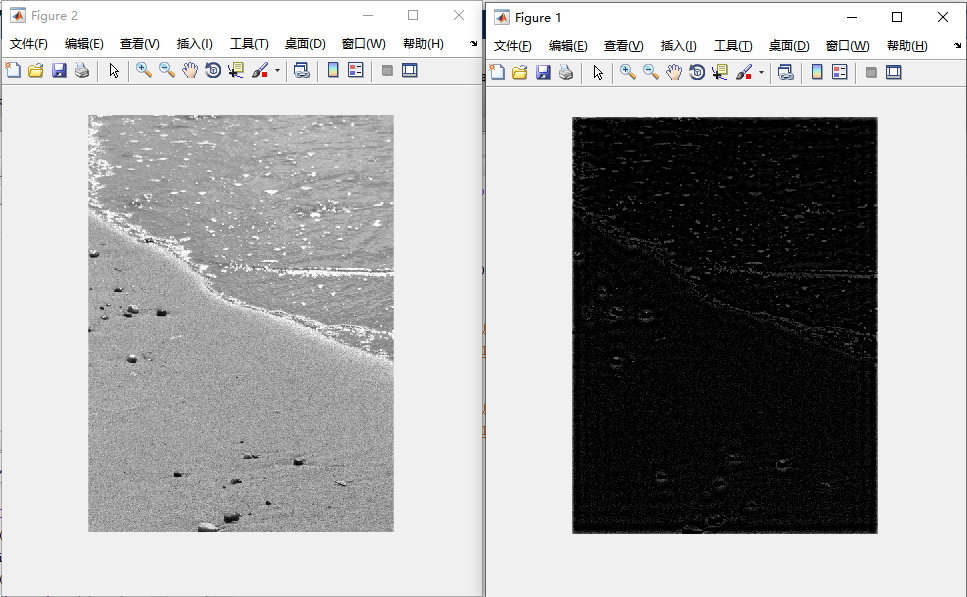
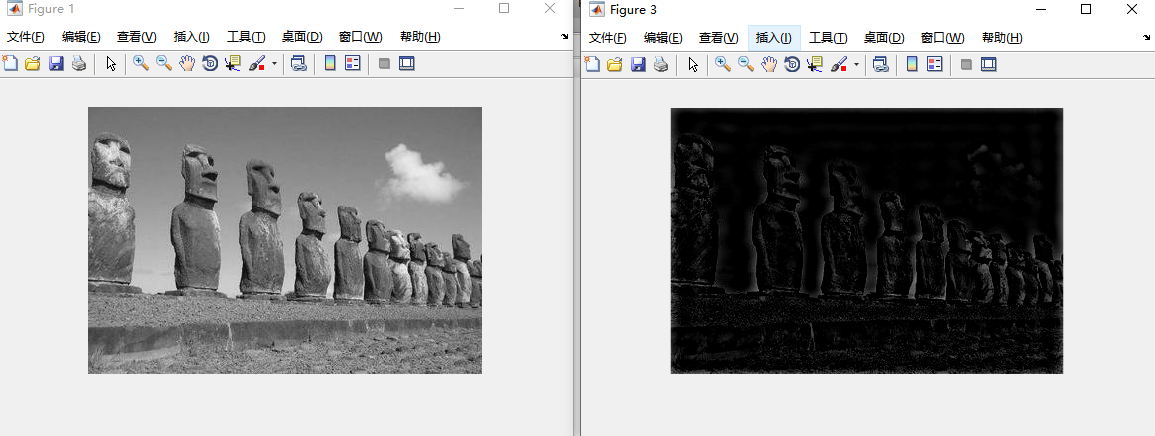
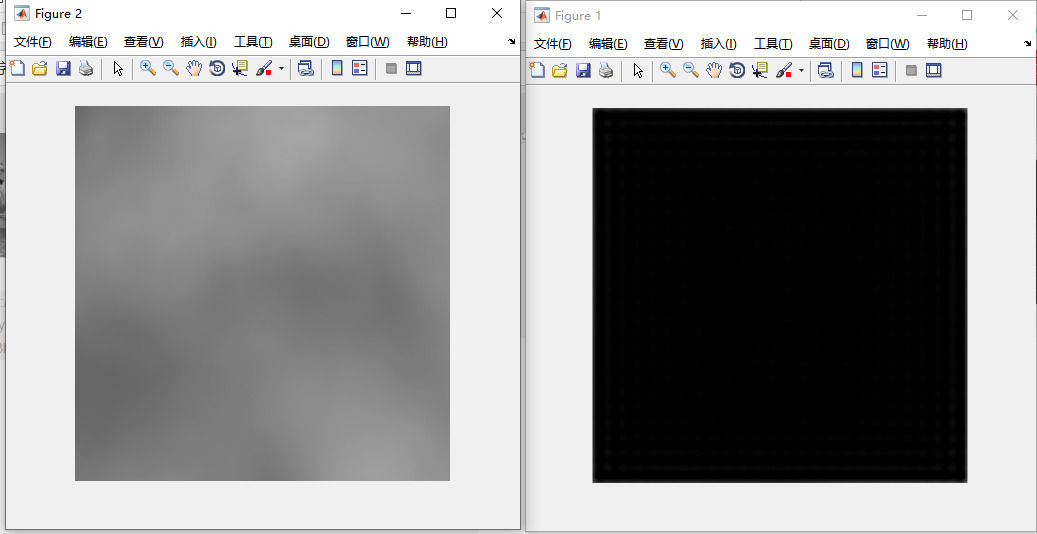
观察三幅经过理想高通滤波器的图像，第一幅沙滩与水面的分界以及沙滩，水面上的细节边缘得到锐化，清晰分明；第二幅图像经过高通滤波后，其中的石像与背景边缘明显；第三幅图像由于本身的边缘细节模糊，经过高通滤波后，低频分量全部得到抑制，得到一幅黑色图像，信息全部丢失，可以通过修改截至频域进行优化。可以看出图像中的边缘和其他灰度急转得到了增强，而消除了模糊的部分，抑制了低频分量，使图像的线条，边沿变得清晰，完成了图像锐化的目的。
三、高频强调滤波器
但是，由于高通滤波器偏离了傅里叶变换的原点，经过高通滤波后，图像都是去了大部分原始图像中呈现的灰度，这是需要进行高频强调滤波。
高频强调滤波的原理是基于原始高频滤波器传递函数的。原始高频强调滤波器的传递函数为H(u,v),则高频强调滤波的传递函数是a+bH(u,v)。
通过对高通滤波器补偿一个偏移量，再有一个大于1的常数乘数来突出高频部分，来构成一个高频强调滤波器。
一个高频强调滤波器的实例：
clear all
>> f=imread('C:/experiment/test11.jpg');
>> f=rgb2gray(f);
>> PQ=paddedsize(size(f));
>> D0=0.05*PQ(1);
>> HBW=hpfilter('btw',PQ(1),PQ(2),D0,2);
>> H=0.5+2*HBW;
>> gbw=dftfilt(f,HBW,'fltpoint');
>> gbw=gscale(gbw);
>> ghf=dftfilt(f,H,'fltpoint');
>> ghf=gscale(ghf);
>> figure,imshow(gbw)
>> figure,imshow(ghf)
>> figure,imshow(f)
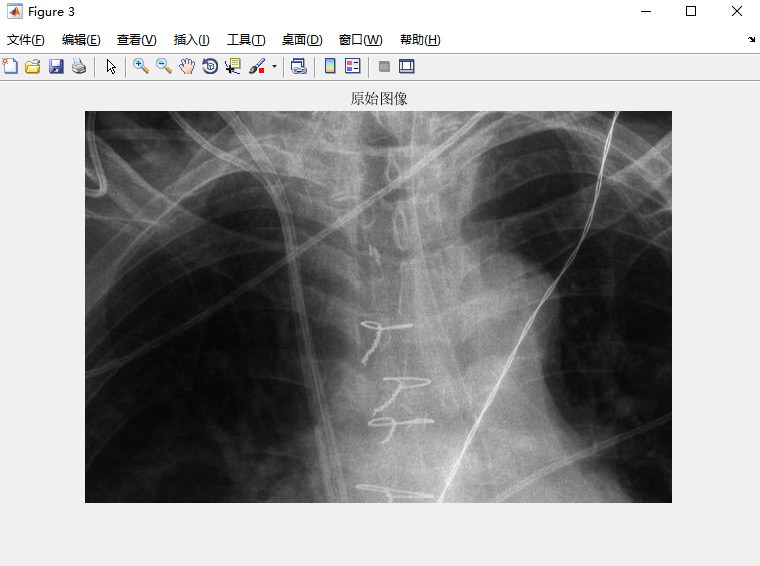
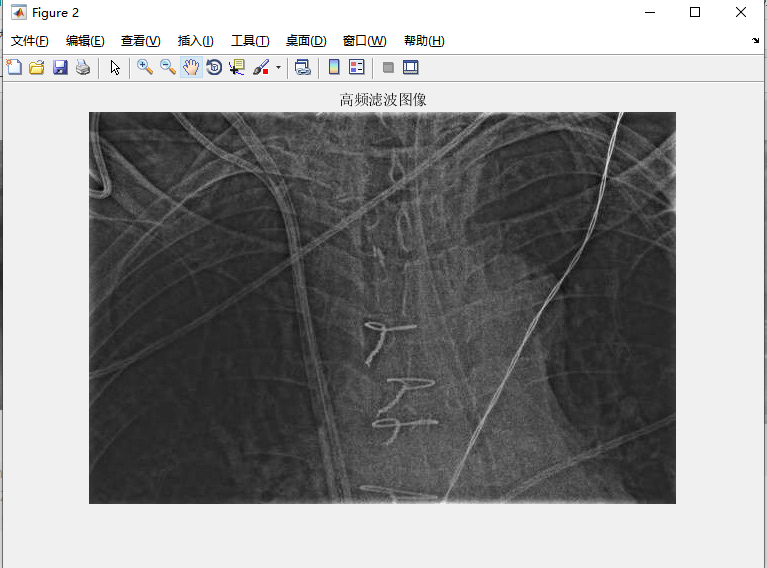
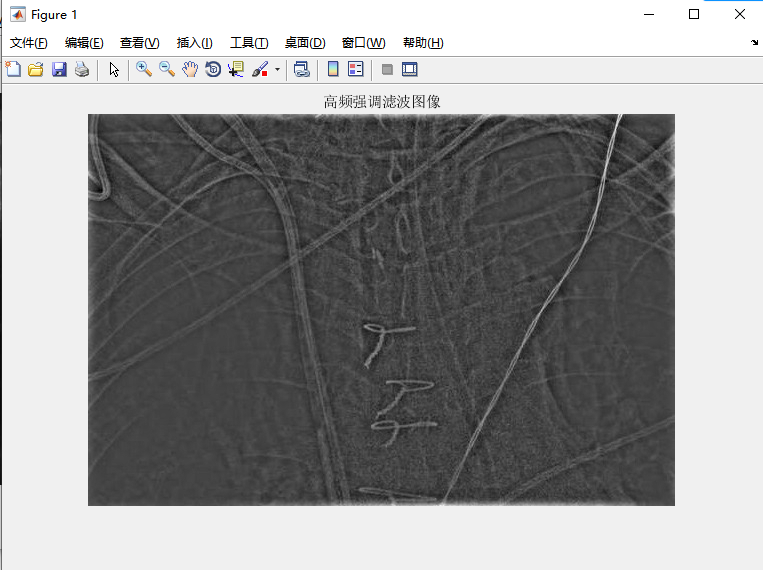
后两幅图像显示了对初始图像的滤波结果，所用的是一个二阶巴特沃斯滤波器，D0的值等于填充后的图像的垂直长度的0.05倍。第二幅图像是高频滤波的结果，第三幅图像是高频强调滤波的结果。一幅非零图像具有零均值的唯一方法是，该图像的某些灰度值为负，即如同第二幅图像显示结果。因此，必须在dftfilt中使用fltpoint选项来得到浮点型结果，否则会失去一些细节。
观察得知，高频滤波丢失了一些原始图像低频分量引起的灰色调，而在高频强调滤波中得以保留。图像的一些主要边缘仍然有些模糊，在高频强调滤波中，得到了改善。
最后
以上就是拉长宝贝为你收集整理的四、基于MATLAB的数字图像处理————频率域滤波（二）的全部内容，希望文章能够帮你解决四、基于MATLAB的数字图像处理————频率域滤波（二）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复