MATLAB 图像滤波器

72 阅读 0 评论 48 点赞

我是靠谱客的博主眯眯眼白羊，最近开发中收集的这篇文章主要介绍MATLAB 图像滤波器，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

实验目的

– 继续熟悉仿真工具MATLAB

– 巩固图像读取与显示的方法

– 掌握给图像添加噪声的方法

– 掌握图像空间域的滤波方法

– 掌握图像频率域的滤波方法

实验原理

空间域平滑操作

(1)高斯噪声是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声。

(2)椒盐噪声，椒盐噪声又称脉冲噪声，它随机改变一些像素值，是由图像传感器，传输信道，解码处理等产生的黑白相间的亮暗点噪声。椒盐噪声往往由图像切割引起。

(3)均值滤波算法是比较常用，也比较简单的滤波算法。在滤波时，将N个周期的采样值计算平均值，算法非常简单。当N取值较大时，滤波后的信号比较平滑，但是灵敏度差；相反N取值较小时，滤波平滑效果差，但灵敏度好。

(4)中值滤波是一种典型的非线性滤波，是基于排序统计理论的一种能够有效抑制噪声的非线性信号处理技术，基本思想是用像素点邻域灰度值的中值来代替该像素点的灰度值，让周围的像素值接近真实的值从而消除孤立的噪声点。该方法在取出脉冲噪声、椒盐噪声的同时能保留图像的边缘细节。这些优良特性是线性滤波所不具备的。

空间域锐化操作

(1)Sobel算子是像素图像边缘检测中最重要的算子之一。在技术上，它是一个离散的一阶差分算子，用来计算图像亮度函数的一阶梯度之近似值。在图像的任何一点使用此算子，将会产生该点对应的梯度矢量或是其法矢量。

(2)Prewitt算子是一种一阶微分算子的边缘检测，利用像素点上下、左右邻点的灰度差，在边缘处达到极值检测边缘，去掉部分伪边缘，对噪声具有平滑作用。其原理是在图像空间利用两个方向模板与图像进行邻域卷积来完成的，这两个方向模板一个检测水平边缘，一个检测垂直边缘。

(3)Laplacian算子是n维欧几里得空间中的一个二阶微分算子，定义为梯度grad（）的散度div（）。因此如果f是二阶可微的实函数，则f的laplacian算子定义为：f的拉普拉斯算子也是笛卡尔坐标系xi中的所有非混合二阶偏导数求和：作为一个二阶微分算子，拉普拉斯算子把C函数映射到C函数，对于k ≥ 2。

3.图像的频域处理

(1)低通滤波

低通滤波可以简单的认为：设定一个频率点，当信号频率高于这个频率时不能通过，在数字信号中，这个频率点也就是截止频率，当频域高于这个截止频率时，则全部赋值为0。因为在这一处理过程中，让低频信号全部通过，所以称为低通滤波。在数字图像处理领域，从频域看，低通滤波可以对图像进行平滑去噪处理。

(2)高通滤波

高通滤波是只对低于某一给定频率以下的频率成分有衰减作用，而允许这个截频以上的频率成分通过，并且没有相位移的滤波过程。主要用来消除低频噪声，也称低截止滤波器。

高通滤波属于[频率域]滤波，它保留高频，抑制低频，是[图像锐化]的一种方式。

（3）傅里叶变换

频率中最典型的就是傅立叶变换，傅立叶变换能把图像从空间域变换到只包含不同频率信息的频率域，原图像上的灰度突变部位、图像结构复杂的区域、图像细节及干扰噪声等信息集中在高频区，而原图像上灰度变化平缓部位的信息集中在低频区。

三、实验环境

– Windows XP/ Windows 7

– Matlab 7.0.1/ Matlab R2008

四、实验内容与步骤

– （1）空间域平滑操作

 读取并显示一幅灰度图像；

 对原图像分别添加高斯噪声和椒盐噪声，并显示添加噪声之后的图像；调整高斯噪声和椒盐噪声的参数，比较不同参数之间噪声的区别；

 针对两幅含有噪声的图像，分别采用3*3、5*5、7*7平均模板和高斯模板进行平滑操作，观察、记录并比较实验结果；

 针对两幅含有噪声的图像，采用中值滤波方法进行平滑处理，观察并记录实验结果。并将之与上一步骤的实验结果相比较，得出相关结论。

读取peppers图像，加入标准差为0.1的高斯噪声

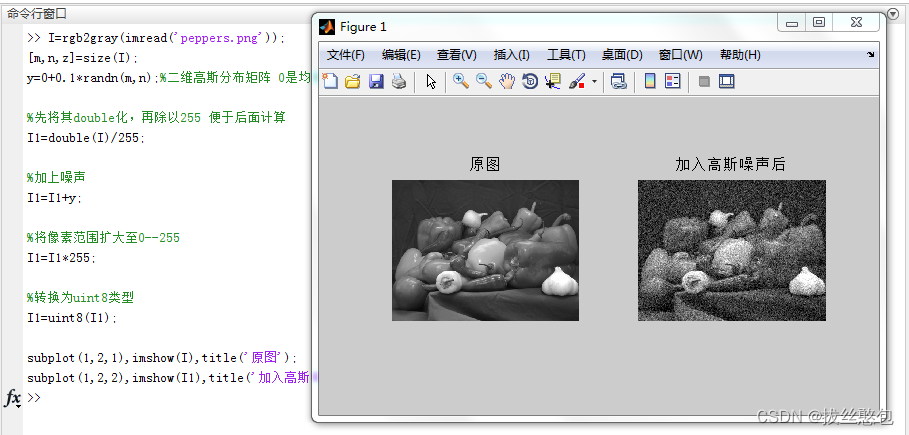
加入标准差为0.3的高斯噪声：

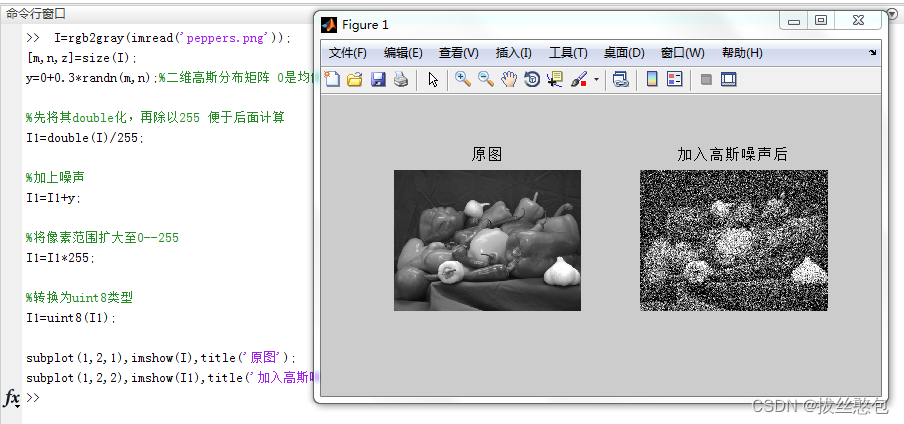
标准差越高，图像的噪声越大，颗粒感更强。

加入密度不同的椒盐噪声：

加入密度分别为0.1、0.2、0.3的椒盐噪声：

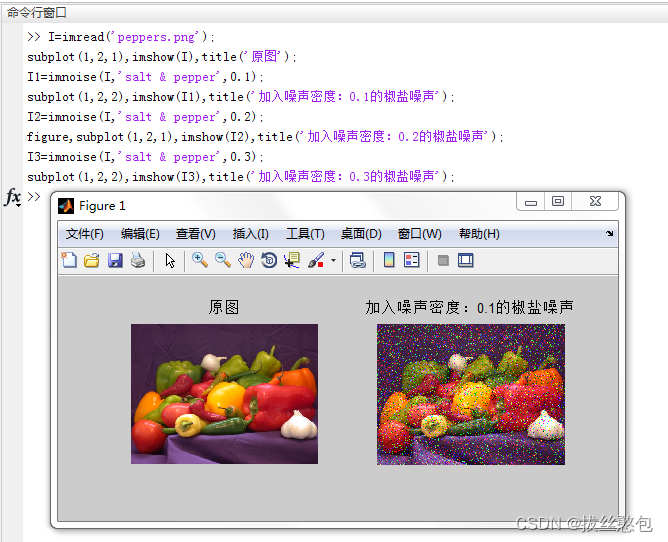
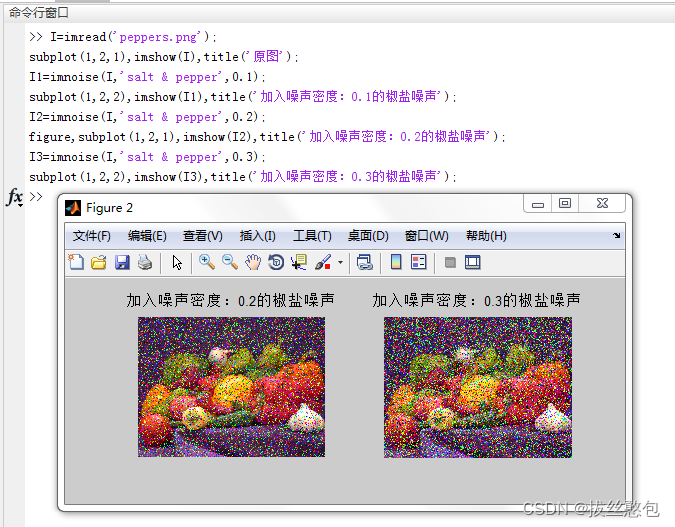
加入的椒盐噪声密度越大，图像越像“电视花了”，也就是“椒”和“盐”分布的更密集了。

对比

椒盐噪声是数字图像的一个常见噪声，所谓椒盐，椒就是黑，盐就是白，椒盐噪声就是在图像上随机出现黑色白色的像素。

高斯噪声是指它的概率密度函数服从高斯分布（即正态分布）的一类噪声。常见的高斯噪声包括起伏噪声、宇宙噪声、热噪声和散粒噪声等等。

采用3*3、5*5、7*7平均模板进行平滑操作

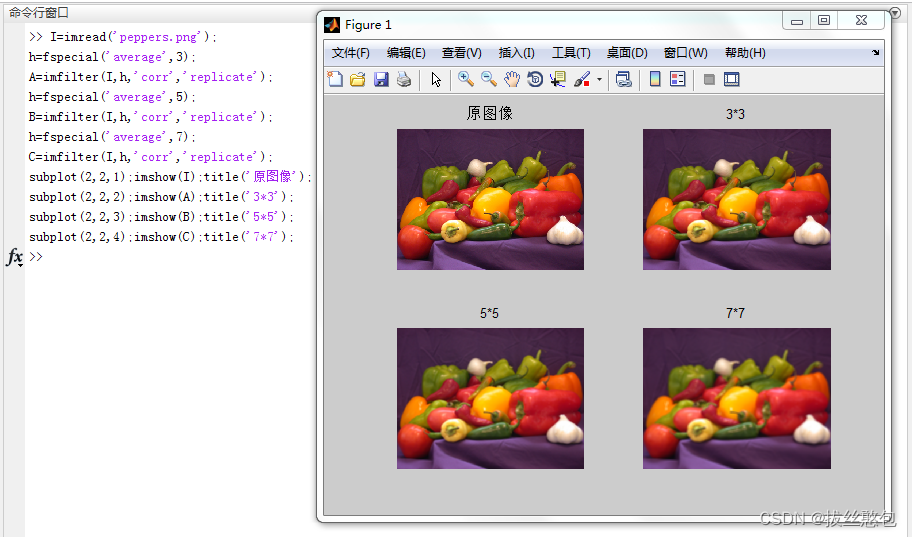
采用高斯模板进行平滑操作

读入cameraman图像，对其采用高斯模板进行平滑操作：

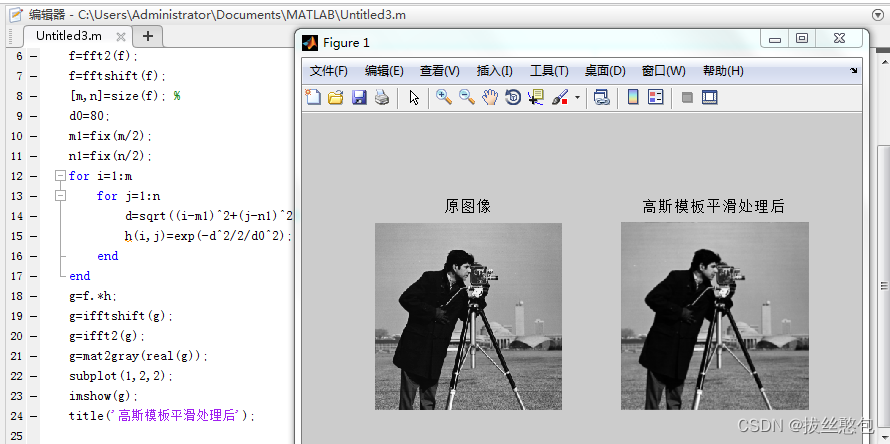
高斯噪声的幅值近似正态分布，但是分布在每个点上。因为所有的点都被污染所以不能中值滤波选不到正确的干净的点。因为高斯噪声服从正态分布所以均值噪声为零可以选用均值滤波处理噪声。

针对两幅含有噪声的图像采用中值滤波方法进行平滑处理

同样对于cameraman图像，采用中值滤波方法进行平滑：

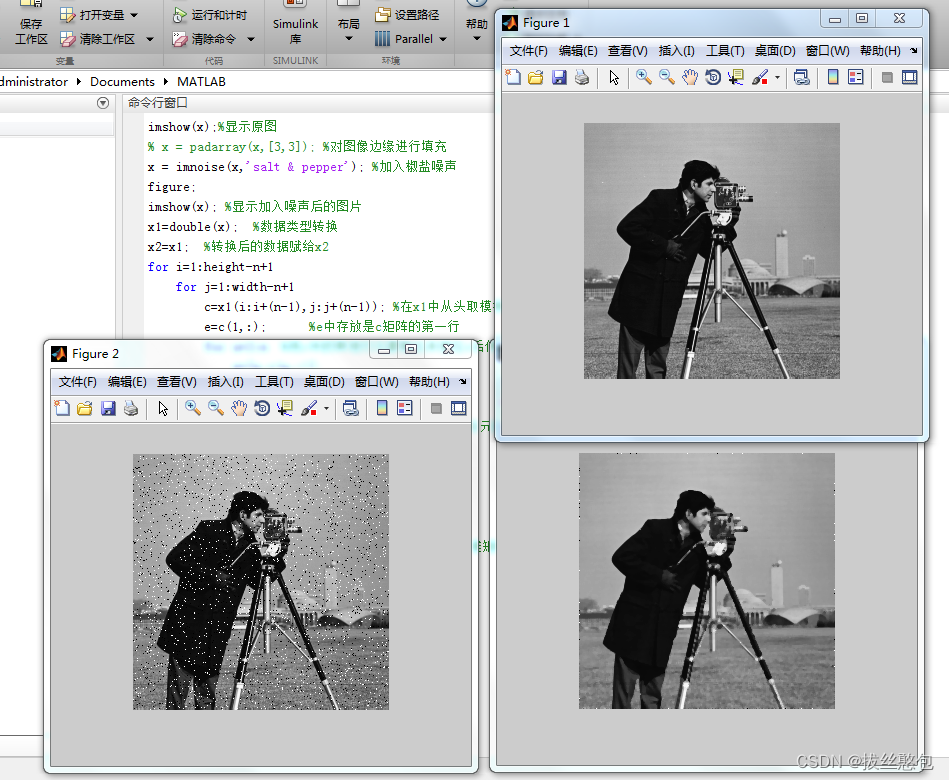
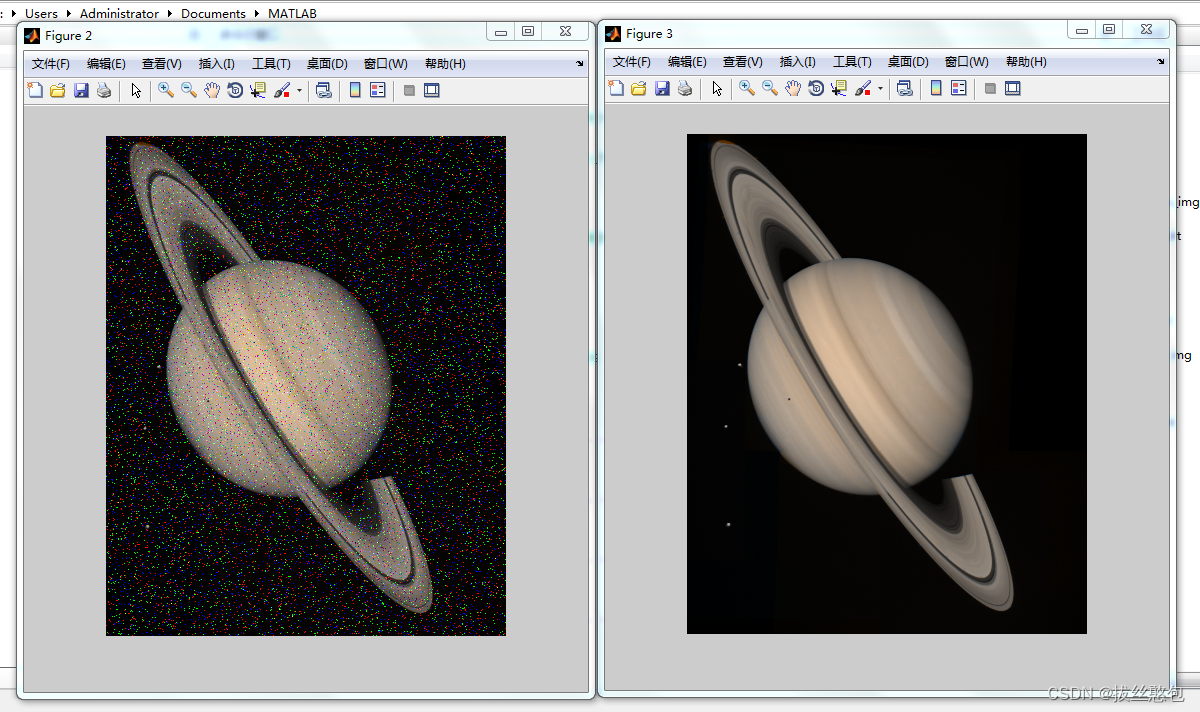
对于含有椒盐噪声的图像，适合中值滤波。椒盐噪声是幅值近似相等但是随机的分布在不同位置，图中既有污染的点，也有干净的点。图中噪声的均值不为零，所以不适合均值滤波。正因为图中有干净的点也有污染的点，所以中值滤波可以用干净的点代替污染的点。

– （2）空间域锐化操作

 读取并显示一幅灰度图像；

 分别采用Prewitt水平/垂直边缘检测算子，Sobel水平/垂直边缘检测算子对原图像进行锐化操作，比较实验结果；

 采用拉普拉斯模板进行锐化处理，与上一步骤实验结果相比较。

采用Prewitt算子进行锐化

I=imread(‘saturn.tif’);
I1=rgb2gray(I); %将彩色图变成灰色图
subplot(131);
imshow(I1),title(‘原图’);
model=[-1,0,1;
-1,0,1;
-1,0,1];
[m,n]=size(I1);
I2=I1;
for i=2:m-1
for j=2:n-1
tem=I1(i-1:i+1,j-1:j+1);
tem=double(tem).*model;

I2(i,j)=sum(sum(tem));
end
end
subplot(132),
imshow(uint8(I2)),title(‘边缘提取后的图像’);
I2=I2+I1;
subplot(133),
imshow(I2),title(‘图像锐化’);

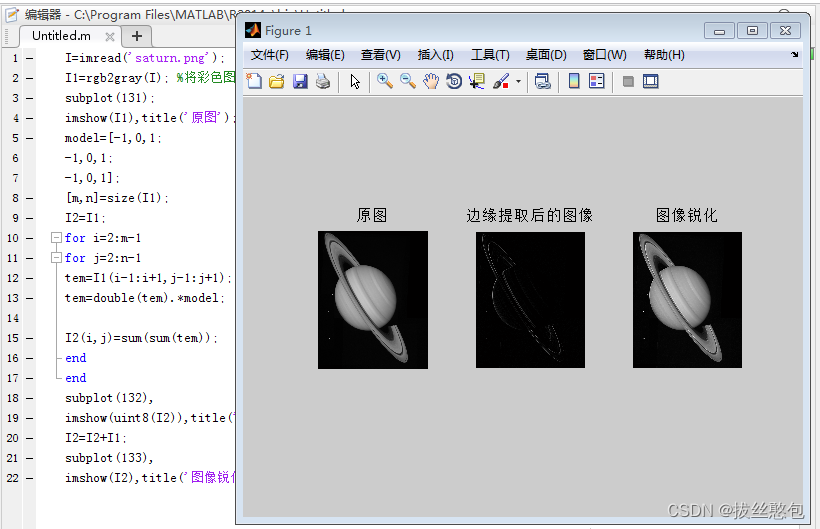
2.采用Sobel算子进行锐化

I=imread(‘saturn.png’); %读取图像
I1=rgb2gray(I); %将彩色图变成灰色图
imshow(I1),title(‘原图’);

model=[-1,0,1;
       -2,0,2;
       -1,0,1];
[m,n]=size(I1);
I2=double(I1);

for i=2:m-1
    for j=2:n-1
        I2(i,j)=I1(i+1,j+1)+2*I1(i+1,j)+I1(i+1,j-1)-I1(i-1,j+1)-2*I1(i-1,j)-I1(i-1,j-1);
    end
end
figure,
imshow(I2),title(‘边缘提取后的图像’);
I2 = I2 + double(I1);
figure,
imshow(uint8(I2)),title(‘锐化后的图像’);

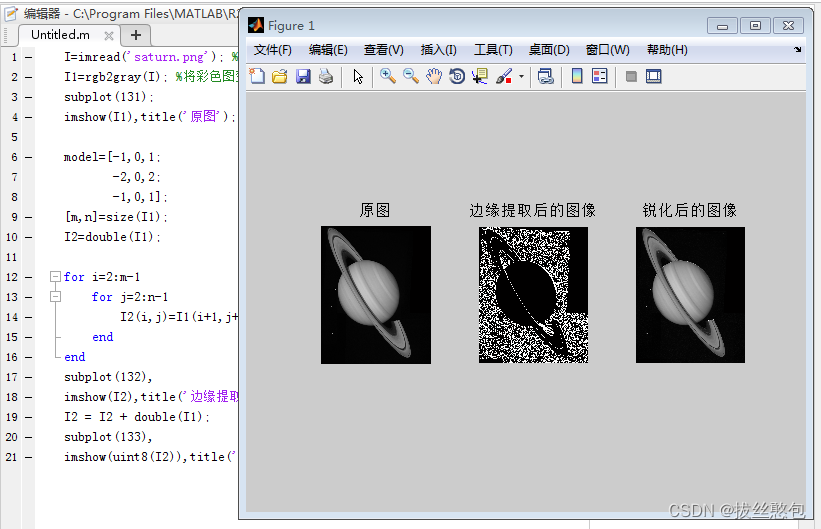
3. 采用拉普拉斯模板进行锐化处理

I=imread(‘saturn.png’);
I1=mat2gray(I);%实现图像矩阵的归一化操作
[m,n]=size(I1);
newGrayPic=I1;%为保留图像的边缘一个像素
LaplacianNum=0;%经Laplacian算子计算得到的每个像素的值
LaplacianThreshold=0.2;%设定阈值
for j=2:m-1 %进行边界提取
    for k=2:n-1
        LaplacianNum=abs(4*I1(j,k)-I1(j-1,k)-I1(j+1,k)-I1(j,k+1)-I1(j,k-1));
        if(LaplacianNum > LaplacianThreshold)
            newGrayPic(j,k)=255;
        else
            newGrayPic(j,k)=0;
        end
    end
end
I2=rgb2gray(I); %将彩色图变成灰色图
subplot(131),imshow(I2),title(‘原图’);
subplot(132),
imshow(newGrayPic);
title(‘拉普拉斯边缘提取后’)
t=I1+newGrayPic;
subplot(133),imshow(t),title(‘锐化后的图像’);

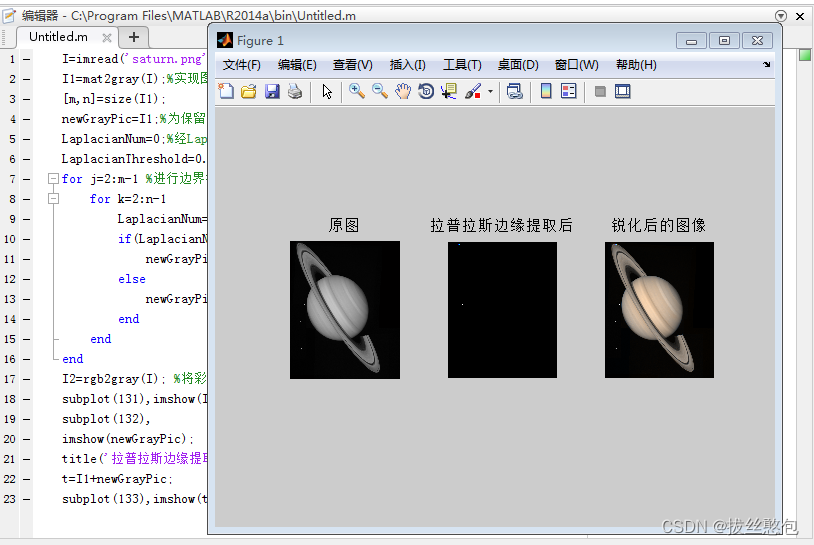
对比：Sobel算子能够锐化的边缘信息较强；

Prewitt算子有一定的抗干扰性，图像效果比较干净；

Laplacian算法是线性二次微分算子，与梯度算子一样具有旋转不变性，从而满足了不同方向的图像边缘锐化要求，其获得的边界比较细，包括较多的细节信息，但边界不清晰。

– （3）图像的频域处理

 利用循环语句，自己构建理想低通滤波器；

I = imread(‘cameraman.tif’);
I=rgb2gray(I);
figure(1);
subplot(221),imshow(I);
title(‘原图像’);
I=imnoise(I,’gaussian’);%%加入高斯白噪声
subplot(222),imshow(I);
title(‘加入噪声后’);
s=fftshift(fft2(I));
subplot(223), imshow(log(abs(s)),[]);
title(‘傅里叶变换频谱图’);
[a,b]=size(s);
a0=round(a/2);
b0=round(b/2);
d=50;
for i=1:a
    for j=1:b
        distance=sqrt((i-a0)^2+(j-b0)^2);
        if distance<=d
            h=1;
        else
            h=0;
        end
        s(i,j)=h*s(i,j);
    end
end
s=uint8(real(ifft2(ifftshift(s))));
subplot(224),imshow(s);
title(‘理想低通滤波所得图像’);

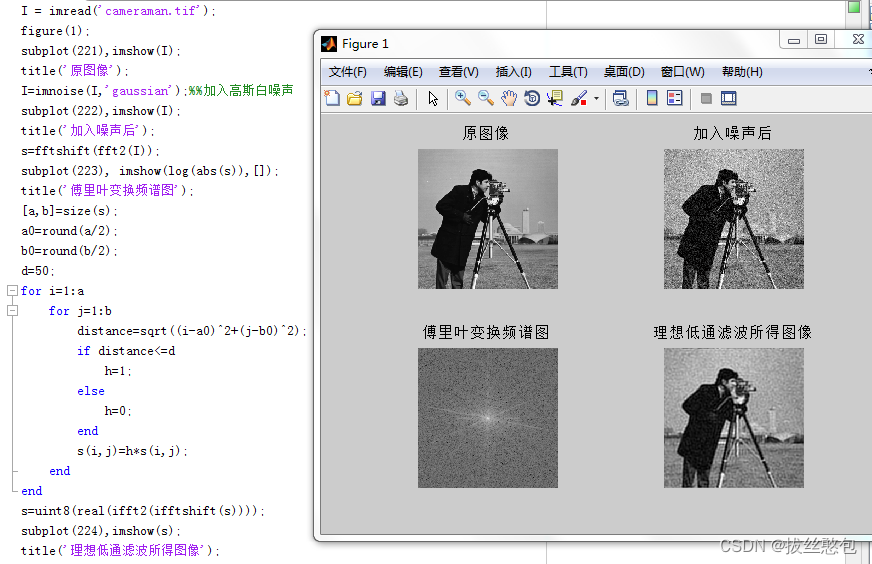
对一幅灰度图像进行傅里叶变换，显示其频谱图；

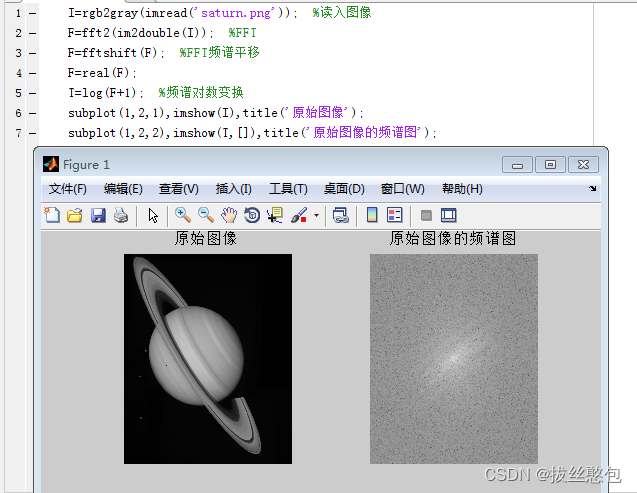
 对一幅灰度图像作频率域理想低通滤波，调整滤波器半径，观察并记录不同结果，分析原因；

d0=50;  %阈值
I=imread(‘cameraman.tif’);
[M ,N]=size(I);

I_f = fft2(double(I));%傅里叶变换得到频谱
I_f=fftshift(I_f);  %移到中间

m_mid=floor(M/2);%中心点坐标
n_mid=floor(N/2);

h = zeros(M,N);%低通滤波器构造
for i = 1:M
    for j = 1:N
        d = ((i-m_mid)^2+(j-n_mid)^2);
        h(i,j) = exp(-(d)/(2*(d0^2)));
    end
end

I_lpf = h.*I_f;

I_lpf=ifftshift(I_lpf);    %中心平移回原来状态
I_lpf=uint8(real(ifft2(I_lpf)));  %反傅里叶变换,取实数部分

subplot(1,2,1);imshow(I);title(‘原图’);
subplot(1,2,2);imshow(I_lpf);title(‘低通滤波d=50’);

低频部分主要是灰度平滑区域，高频部分可能是噪声或者图像边缘特征，主要是灰度变化较大区域。通过低通滤波器，滤除高频部分，保留低频部分，可有效去除噪声。被低通滤波的图像比原始图像少尖锐的细节部分而突出平滑过渡部分。

半径越小，图像越模糊，越平滑。

 利用循环语句，自己构建理想高通滤波器；

I = imread(‘cameraman.tif’);
I=rgb2gray(I);
figure(1);
subplot(221),imshow(I);
title(‘原图像’);
I=imnoise(I,’gaussian’);%%加入高斯白噪声
subplot(222),imshow(I);
title(‘加入噪声后’);
s=fftshift(fft2(I));
subplot(223), imshow(log(abs(s)),[]);
title(‘傅里叶变换频谱图’);
[a,b]=size(s);
a0=round(a/2);
b0=round(b/2);
d=50;
for i=1:a
    for j=1:b
        distance=sqrt((i-a0)^2+(j-b0)^2);
        if distance<=d
            h=0;
        else
            h=1;
        end
        s(i,j)=h*s(i,j);
    end
end
s=uint8(real(ifft2(ifftshift(s))));
subplot(224),imshow(s);
title(‘理想高通滤波所得图像’);

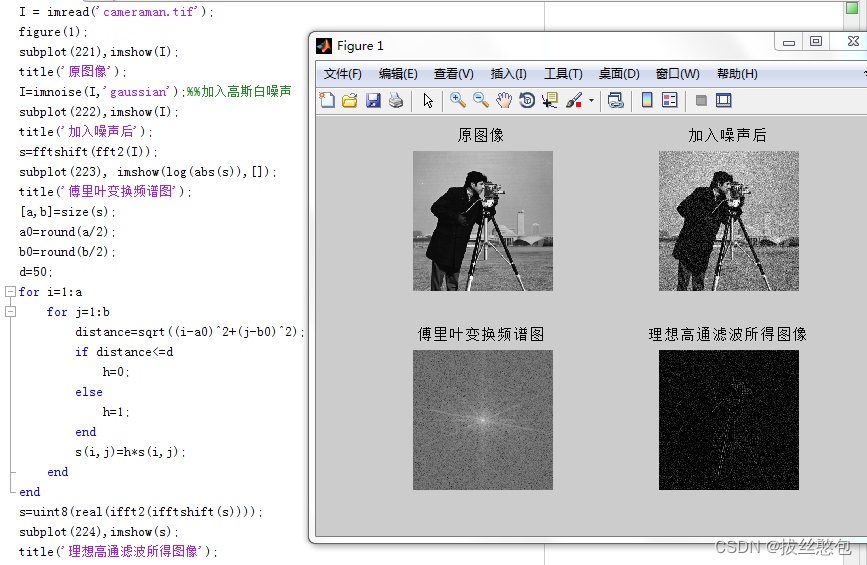
 对同一幅灰度图像作频率域理想高通滤波，调整滤波器半径，观察并记录不同结果，分析原因；

d0=30;  %阈值
I=imread(‘cameraman.tif’);
[M ,N]=size(I);

I_f = fft2(double(I));%傅里叶变换得到频谱
I_f=fftshift(I_f);  %移到中间

m_mid=floor(M/2);%中心点坐标
n_mid=floor(N/2);

h = zeros(M,N);%高斯高通滤波器构造
for i = 1:M
    for j = 1:N
        d = ((i-m_mid)^2+(j-n_mid)^2);
        h(i,j) = 1-exp(-(d)/(2*(d0^2)));
    end
end

I_lpf = h.*I_f;

I_lpf=ifftshift(I_lpf);    %中心平移回原来状态
I_lpf=uint8(real(ifft2(I_lpf)));  %反傅里叶变换,取实数部分

subplot(1,2,1);imshow(I);title(‘原图’);
subplot(1,2,2);imshow(I_lpf);title(‘高通滤波d=30’);

高通滤波器使高频通过而使低频衰减，被高通滤波的图像比原始图像少灰度级的平滑过渡而突出边缘等细节部分。

半径约小，图像边缘更明显。

六、实验心得与体会

本次实验一共分为了三个不同的部分，图像的平滑、锐化和频域处理。虽说划分出了三个部分，但他们之间是紧密联系的。

1.在学习对图像平滑操作时，先学习了如何给图像加入噪声，认识到高斯噪声和椒盐噪声的区别，以及不同参数下两种噪声的变化和对比。接着学习了用均值滤波和中值滤波对含噪声的图像进行平滑处理，发现了这两种不同的平滑方式各自针对不同的噪声有更好的效果：对于含有椒盐噪声的图像，适合中值滤波；对于含有高斯噪声的图像，适合均值滤波。认识到了为了展现更好的效果，要选取合适的图像素材进行处理，不然体会不到明显的区别。

2．接着学习了三种不同的算子对图像的锐化处理，切身感受了不同的算子对图像锐化的侧重点不同，比如Sobel算子能够锐化的边缘信息较强，在今后应用中如果想提取图像的边缘信息最好选用Sobel算子。对于不同的需求，我们应该选用合适的方法，避免浪费时间。

3．对于图像频率域的操作，通过构建理想低通和高通滤波器，体会到了两种不同的滤波方法对图像处理注重的部分是不同的。在写循环语句的时候也体现了出来，当构造好理想低通滤波器之后只需要把圆的0和1值调换就可得到理想高通滤波器。体会到了经过傅里叶变换将图像从空间域转换到频率域之后再处理的巧妙，与课本上的知识再次结合，学到了很多。