????????个人主页:研学社的博客
????????????????欢迎来到本博客❤️❤️????????
????博主优势:????????????博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
????????????本文目录如下:????????????
目录
????1 概述
????2 运行结果
????3 参考文献
????4 Matlab代码及文章讲解
????1 概述
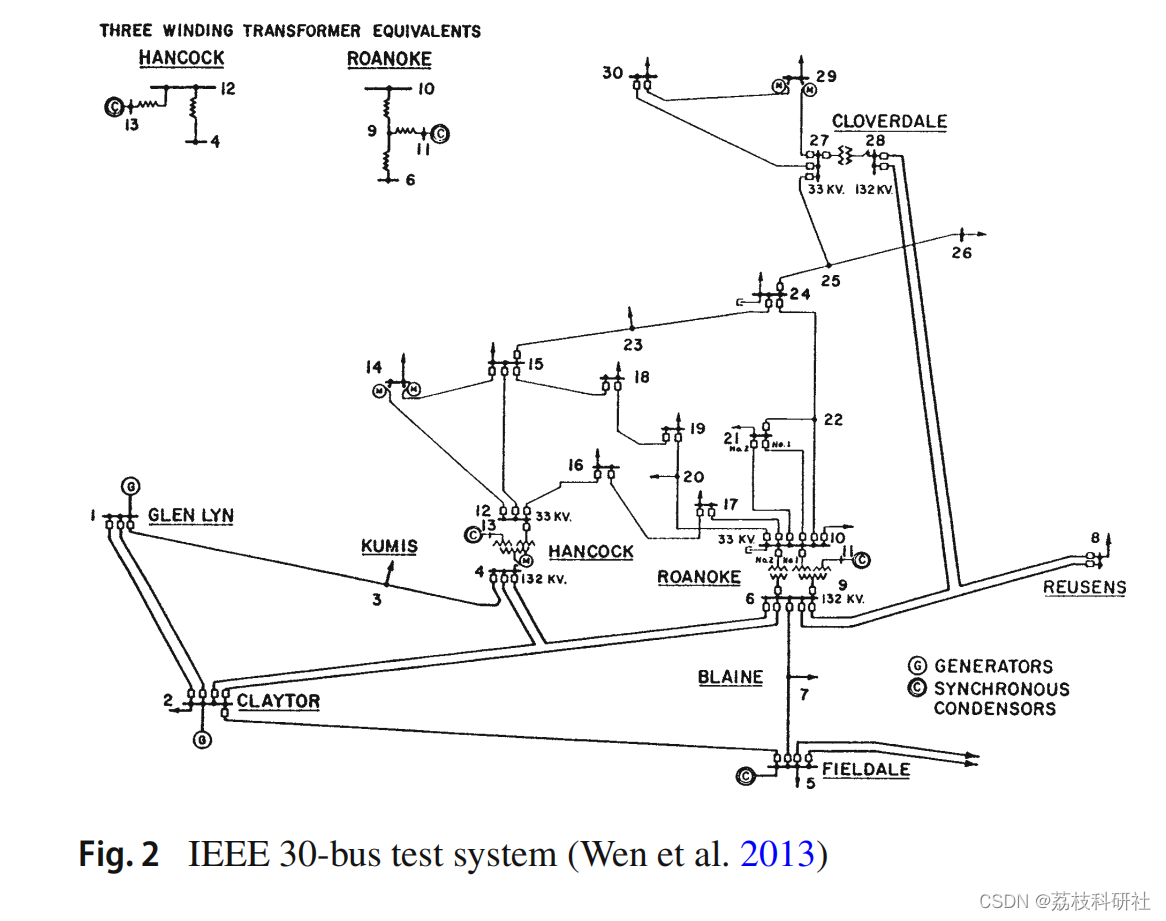
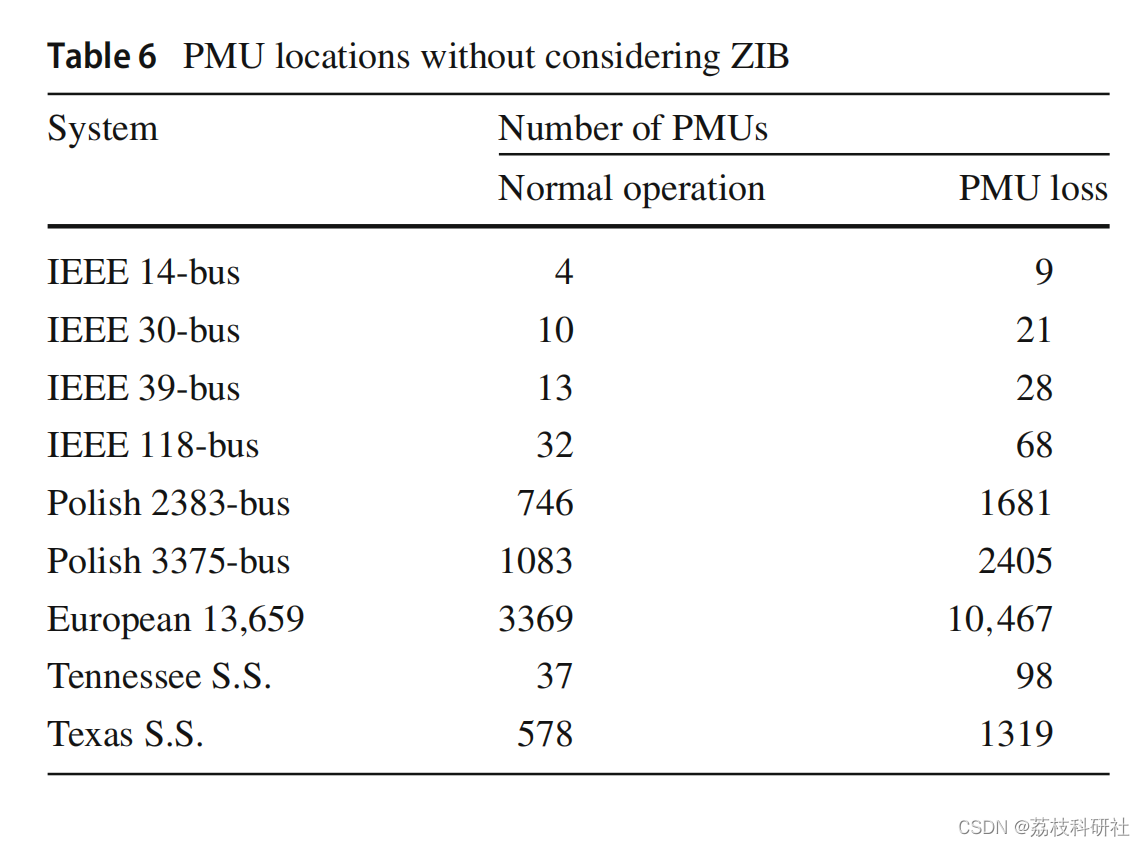
零注入节点 (ZIB) 可以减少为实现完全可观测性而需要安装的相量测量单元 (PMU) 的数量。已经证明,一组相邻的ZIB可以进一步减少所需的PMU数量。与单个 ZIB 相比,除了一些启发式方法外,一组 ZIB 的效果尚未使用数学方法纳入最佳 PMU 放置 (OPP) 模型中。该文提出一种利用整数线性规划方法将一组ZIB效应纳入OPP模型的新方法。还考虑了两种常见的意外情况 - 线路中断和PMU丢失。此外,两种可视化技术用于说明从OPP获得的PMU的位置:(1)使用基于图形的力导向方法和(2)使用地理信息系统在地图上。使用几种小型和大型测试系统验证了所提出的方法,并与其他相关研究进行了比较。
相量测量单元 (PMU) 是智能电子设备,可提供电压和电流的同步相量测量(Mazhari 等人,2013 年)。PMU同步是通过使用全球定位系统(GPS)提供的参考时间信号对电压和电流波形进行时间戳来实现的。PMU是广域测量系统最新技术发展最合适的测量设备(Azizi等人,2013)。限制可安装PMU数量的最具挑战性的障碍是安装成本和通信设施的可用性(Hooshmand等人,2016)。在系统的每条总线上安装PMU既不必要也不经济(Nuqui and Phadke 2005)。安装在总线上的PMU可以测量总线的电压相量(幅度和角度)以及入射到总线中的所有分支电流相量,假设PMU具有足够数量的通道(Manousakis等人,2012)。换句话说,与传统仪表相比,PMU可以使安装它的总线以及所有相邻的总线可观察。最佳 PMU 放置 (OPP) 的目标是确定使整个系统可观察所需的最小 PMU 数量及其位置。
没有发电机或负载的公交车称为零喷射公交车(ZIB)。流向ZIB的所有电流的总和为零。总线集群是一组总线,包括总线本身和所有相邻总线。零注入群集 (ZIC) 是 ZIB 和所有事件总线的组合。ZIB有可能减少完全可观测性所需的PMU安装数量。然而,零注入约束的建模是OPP的主要挑战之一,因为它具有固有的非线性(Dua等人,2008)。
ZIB可分为两种类型:(1)仅连接到负载和/或发电机总线的ZIB,换句话说,其所有相邻总线都是非ZIB;或 (2) 连接到至少一个其他 ZIB 的 ZIB,并且可以形成一组 ZIB。通过考虑第一种ZIB的OPP在文献中被广泛讨论(Aminifar等人,2010年;郭台铭 2008a, b;阿巴西和伊斯梅尔 2009;阿米尼法等人,2011年;查克拉巴蒂和基里亚基德斯 2008;马努萨基斯和科雷斯 2016;黄等, 2014;温等. 2013;阿卜杜勒·拉赫曼和佐巴 2017;阿加伊等人,2015 年)。然而,只有少数研究检查了一组ZIB对OPP模型的影响。这些研究中使用的所有技术都基于智能搜索技术,并且没有包含一组ZIB效应的数学方法。一组ZIB的概念首先由Hajian等人(2007)的作者使用粒子群优化引入。随后,在Aminifar等人(2009)中,作者使用免疫遗传算法来处理一组ZIB。这两项研究的结果表明,考虑一组ZIB可以进一步减少完全可观测性所需的PMU数量。
文献中用于OPP的解决方案可分为两种技术:确定性和启发式。
确定性技术基于模型的数学表示。使用最广泛的确定性技术是整数线性规划(ILP),它可以求解大规模电力系统而不会陷入局部最小值(Gou 2008b;黄等人,2014)。文献中使用的其他确定性技术是整数非线性规划(Gou 2008a),整数二次规划(Chakrabarti等人,2009),加权最小二乘算法(Manousakis和Korres 2013)和基于概率的约束方法(Aminifar等人,2011)。
启发式解决方案是基于搜索的智能方法,用于求解 OPP,而无需模型的数学表示。文献中描述和使用了几种启发式方法,包括遗传算法(Marin 等人,2003 年)、塔布搜索(Koutsoukis 等人,2013 年)、模拟退火(Nuqui 和 Phadke 2005 年)、粒子群优化(Saleh 等人,2017 年)、免疫算法(Aminifar 等人,2009 年)、决策树(Mahmoodianfard 等人,2009 年)和布谷鸟算法(Dalali 和 Kazemi Karegar 2016 年) ).尽管存在一些优点,但启发式方法的主要缺点是这些技术是近似方法,并且由于局部最小值中可能存在陷阱,可能无法实现全局最优(Monti and Muscas 2016)。
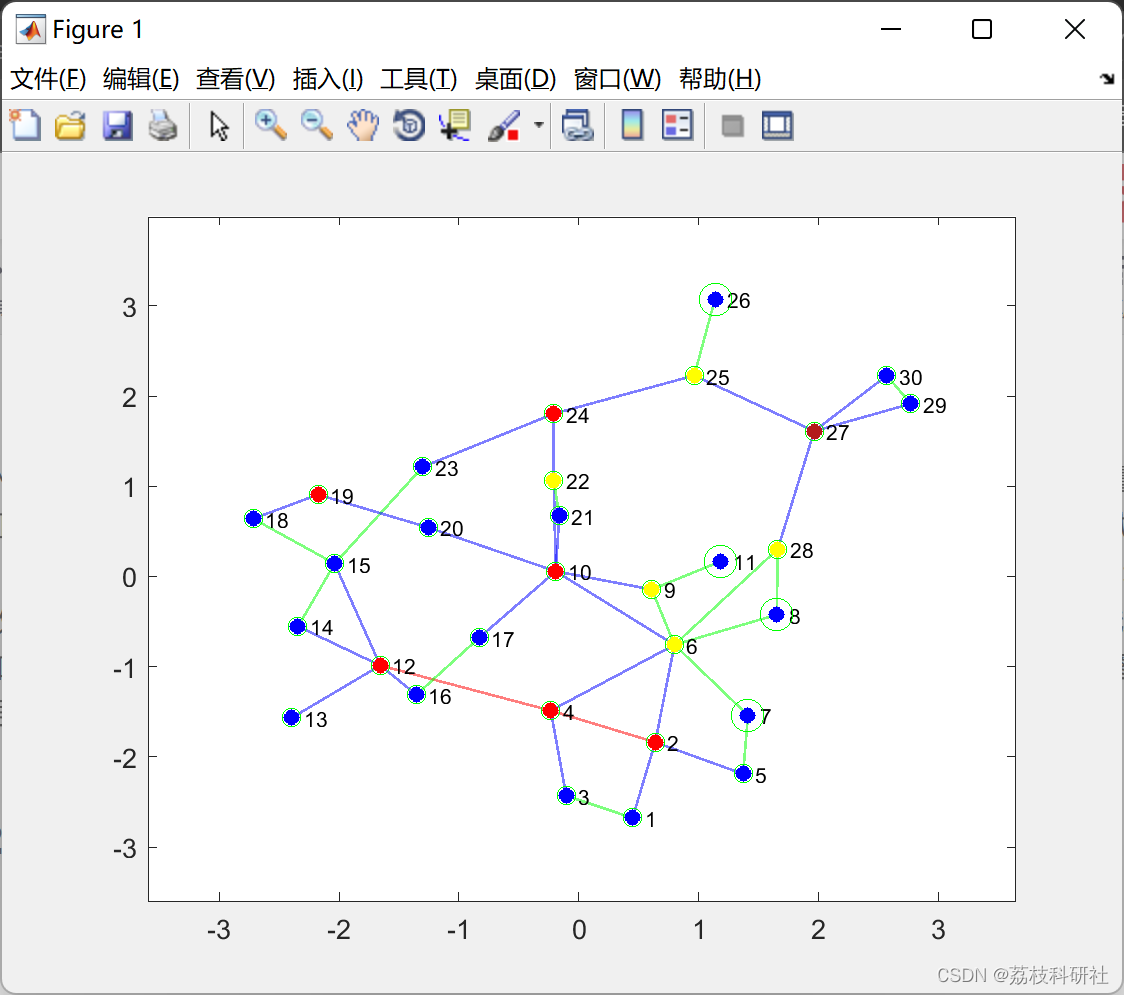
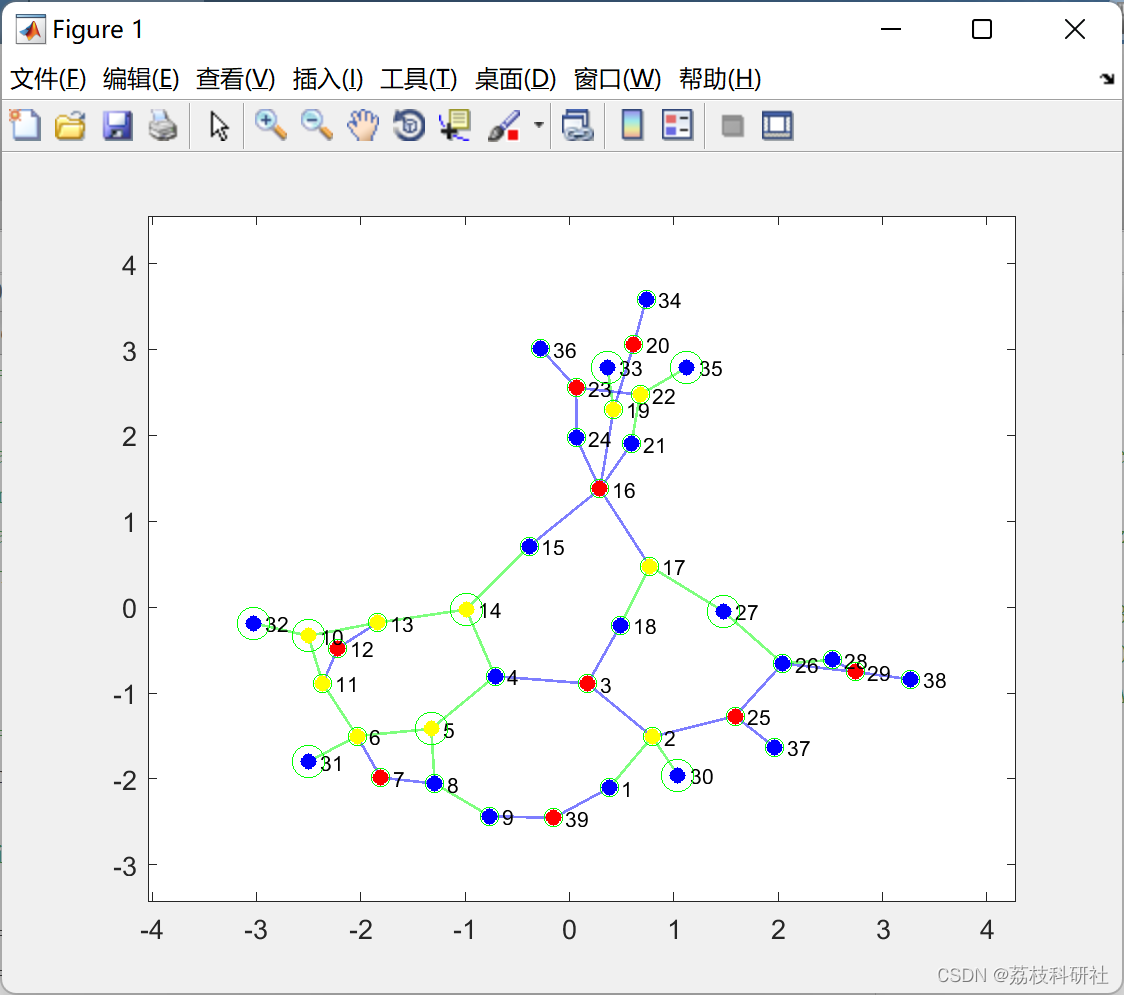
另一个重要的考虑因素是从OPP的数值结果中获得的PMU位置的可视化。在文献中,仅使用表格来说明这些位置。对于波兰测试系统等大型电力系统,PMU的最佳位置在以前的研究中尚未报告。相反,仅提及完全可观测性所需的 PMU 数量。操作员或规划人员可能希望查看地图上可视化的放置结果或图表,以了解问题的详细信息并获得对解决方案的一些见解。这促使我们确定一些技术,以图形和地理方式可视化最佳PMU位置。
本文的主要贡献是:(1)开发一种基于ILP技术的数学方法,将一组ZIB的影响纳入OPP模型,以进一步减少可观测性所需的PMU数量;(2)提出不同的可视化技术,分别利用图论和地理信息系统(GIS)以图形和地图方式说明OPP的数值结果;(3)采用大规模和实用的测试系统,如13,659总线欧洲系统和德克萨斯州和田纳西州的综合测试系统。为了处理多种解决方案,测量冗余被纳入OPP中,以实现最大化目标。此外,通过考虑一组ZIB的影响,不同突发事件(如PMU损失或线路中断)的影响也包含在模型中。将获得的结果与其他七项相关研究进行比较。
本文的其余部分组织如下: 以下部分介绍可观测性规则。在第3节中,制定了基本ILP的数学方程。随后,将单个ZIB的影响合并到方程中。所提出的方法以通用公式为例进行描述和表示。数值结果见第4节。可视化技术在第5节中介绍。最后,结论载于第6节。
基于 PMU 的可观测性分析
如果系统的所有状态都是已知的,即直接测量总线电压相量(幅度和角度)或使用电路规则进行计算,则认为系统是可观察的。电力系统的可观测性可分为两类:数值和拓扑(Huang等人,2014)。数值可观测性可以基于状态估计的增益矩阵进行。如果增益矩阵具有完整的列秩,则称系统是完全可观察的。尽管有一些优点,但高计算负担是数值方法的主要缺点。此外,较大的条件数测量矩阵可能导致不准确的求解。如果存在网络全秩的生成树,则认为该系统在拓扑上是可观测的(Huang et al. 2014)。
拓扑可观测性可以通过应用以下通用规则来实现(Hajian et al. 2007):
- (一)
如果总线安装了测量该总线电压相量的PMU,则认为该总线可直接观察到。如果该PMU还具有用于测量连接到总线的线路的电流相量的通道,则认为线路电流可直接测量。
- (二)
如果线路一端的电压和电流相量已知,则可以使用欧姆定律计算线路另一端的电压相量。这条具有计算电压相量的总线被认为是间接可观测的。
- (三)
如果线路两端的电压相量直接或间接已知,则可以计算该线路的电流相量,假设线路阻抗已知。该线路电流被认为是可间接测量的。
- (四)
对于单个可观测的ZIB,如果该总线和所有相邻总线的电压相量已知,则可以使用ZIB处的基尔霍夫电流定律计算未知电压相量。
- (五)
对于单个不可观测的ZIB,如果其所有相邻总线的电压相量已知,则ZIB也被认为是可观测的,因为它的电压相量可以使用节点方程计算。
- (六)
对于一组不可观测的ZIB,如果所有相邻总线的电压相量已知,则该组中的所有总线都被认为是可观测的,因为它们的电压相量可以使用节点方程计算。
前三个规则是一般规则,可以应用于系统中的任何总线。单个ZIB(ZIB的第1类)的效果由规则(d)和(e)表示。这两个规则可以与以下语句结合使用:如果 ZIC 中的所有总线都是可观察的,除了一条总线之外,也可以使用 ZIB 上的节点方程观察到异常。这表明仅观察(n−1)(n−1)ZIC 中的总线使整个集群可观察,包括不可见的总线,其中 n 是集群中的总线总数。因此,ZIB可以减少完全可观测性所需的PMU数量。最终规则考虑了一组(或多个)ZIB的影响,这可以进一步导致具有较少PMU数量的可观察系统。试图使用ILP将这一规则纳入OPP公式。
????2 运行结果
部分代码:
ZIB4=ZIB2;
ZIB40=zeros(length(ZIB4),length(Y1(1,:)));
ZIB40(:,(ZIB4))=1;
ZIB40=sparse(ZIB40);
ZIB2 = unique(ZIB2);
B=zeros(length(Y1(1,:)), length(Y1(1,:)));
B(sub2ind(size(B), ZIB2, ZIB2))=-1; % replacing ZIB-diagonal elements of Y with a unity
B=sparse(B);
D=-Y1(ZIB,:);
Y1=sparse(Y1);
D=sparse(D);
b1=-ones(1,length(Y1(1,:)));
b3=-ones(1,length(Y1(1,:))); % for cases without considering ZIBs
CC=sparse(zeros(size(Y1))); % for cases without considering ZIBs
b10=zeros(size(b1));
b1(ZIB2)=0;
b10(ZIB2)=-1;
C=sparse(zeros(size(D)));
b1=sparse(b1);
b10=sparse(b10);
BA2=zeros(size(Y1));
BA2(ZIB2,:)=Y1(ZIB2,:);
%=========================================================================
k=1; % k=1 for normal operation, k=2 for contingency operation
A=[Y2 -k*B; C -D]; % see the diff. if Y2 is replaced by Y1 (when no ZIB is considered)
b2=-sparse(ZIB3);
b=[k*b1 b2];
Aineq=A;
bineq=b';
% Note: For a system without ZIB or without considering the effect of ZIB:
% either (1) set Z =0 at the beginning above inside the loop AND (2) replace Y2 with Y1 in A matrix above
% or (1) change B to CC AND (2) change b1 to b3 AND (3) delete C D in the lines above AND (4) replace Y2 with Y1 in A matrix above
%===================Redundancy Consideration (weighting)===================
wr=Count2; % redundancy weight
w0=zeros(1,length(Y1(1,:)));
wt=[wr.^1 wr];
wrc=1/length(Y1(1,:));
w1=[wr.^0 w0];
w2=1/length(A(1,:))*(wt')';
f=wrc+1*(1*w1-1*w2); % the minus is to maximize the redundancy
%================================Solver====================================
options = cplexoptimset;
options.Display = 'on';
x= cplexbilp(f,Aineq,bineq,[],[],[]);
t_end=toc; % time in sec. consumed to solve the problem
x2= find(int16(x));
x3= (x2(x2<=length(Y1(1,:))));x3=x3';
x4=zeros(1,length(Y1(1,:))); x4(x3)=1;
PMU_Locations_and_TotalNo=[x3 length(x3)] % OPP results (locations and total of PMUs)
t_end % display time consumed
%================================PLOTTING==================================
S00=Y1;S00=S00(x3,:);S0=sum(S00); % no. of times nodes observed by PMU
S1=-sum(S0); % sum of no. of times observed buses
S2=sum(S0==0); % no. of unobserved buses (but obsrvable through the effect of ZIB)
S3=find((S0==0)); % locations of unobservable nodes
S=[S1 S2];
% SS(i)=sum(sum(Y(:))==0);% maximize no. of S2
%=============================Lines Statistics=============================
ft=[fb tb];
branch_0PMU0=(ft(find(sum(x4(ft)~=0,2)==0)',:))'; % branches with no PMU installed at ends
branch_1PMU0=(ft(find(sum(x4(ft)~=0,2)==1)',:))'; % branches with one PMU installed at ends
branch_2PMU0=(ft(find(sum(x4(ft)~=0,2)==2)',:))'; % branches with two PMU installed at ends
branch_0PMU=reshape(branch_0PMU0, 1, 2*length(branch_0PMU0(1,:)));
branch_1PMU=reshape(branch_1PMU0, 1, 2*length(branch_1PMU0(1,:)));
branch_2PMU=reshape(branch_2PMU0, 1, 2*length(branch_2PMU0(1,:)));
Y1(logical(eye(size(Y1)))) = 0;
G = graph(Y1~=0);
sz=5;
????3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Abdulrahman, Ismael & Radman, Ghadir. (2018). ILP-Based Optimal PMU Placement with the Inclusion of the Effect of a Group of Zero-Injection Buses. 29. 10.1007/s40313-018-0389-4.
????4 Matlab代码及文章讲解
最后
以上就是畅快画笔最近收集整理的关于基于ILP的最优PMU放置优化研究(Matlab代码实现)的全部内容,更多相关基于ILP内容请搜索靠谱客的其他文章。









发表评论 取消回复