【数字图像处理笔记（七）】之冲激和取样的傅里叶变换

本文章由公号【开发小鸽】发布！欢迎关注！！！

老规矩–妹妹镇楼：

一． 冲激和取样特性

（一）连续冲激的定义

       线性系统和傅里叶变换研究的核心是冲激及其取样特性。连续变量t在t= 0处的单位冲激表示：

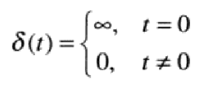
满足等式

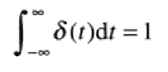
       物理上，如果我们把t解释为时间，那么一个冲激可看成是幅度无限、持续时间为0.具有单位面积的尖峰信号。一个冲激具有关于如下积分的所谓取样特性:

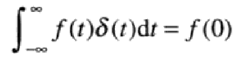
       假设f(t)在t = 0处是连续的，取样特性得到函数f(t)在冲激位置的值。

更一般的取样特性：
       位于任一点t0的冲激，与f(t)相乘，得到任意点冲激位置的函数值：

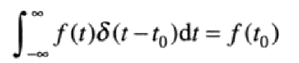
（二）离散冲激的定义

单位离散冲激：

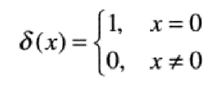
同样满足等式：

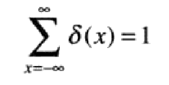
离散变量的取样特性：

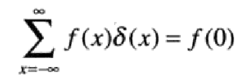
一般的取样特性：

       任意位置的离散冲激取样特性可以得到任意冲激位置处的函数值。

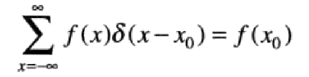
（三）冲激串

       无限个分离的周期冲激单元之和

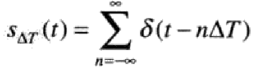
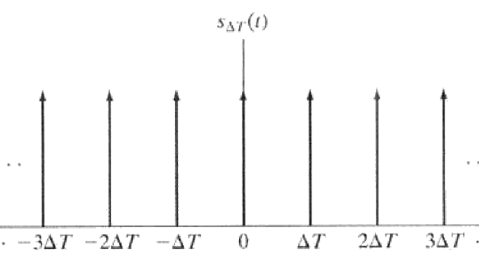
冲激串的示例：

二． 傅里叶变换

（一）连续函数的傅里叶变换

       连续变量t的连续函数f(t)的傅里叶变换：

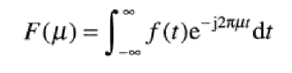
       给定F(u)，通过傅里叶反变换可以得到f(t)：

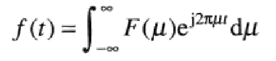
       说明函数可以由变换来恢复。

（二）冲激和冲激串的傅里叶变换

1. 冲激的傅里叶变换

       位于原点的单位冲激的傅里叶变换为：

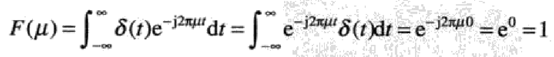
       可以得出，一个位于空间域原点的冲激的傅里叶变换，在频率域是一个常数。

       一般情况下，任意位置的冲激的傅里叶变换为：

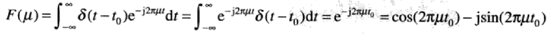
       最后一步由欧拉公式得到。

2. 冲激串的傅里叶变换

       周期为△T的冲激串的傅里叶变换还是冲激串，其周期为1 / △T。

三． 卷积

（一） 连续函数的卷积

       两个连续函数f(t)和h(t)的卷积：

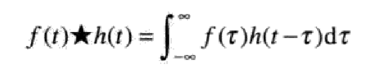
       t是一个函数滑过另一个函数的位移。

（二）卷积定理

       再将两个函数的卷积经过傅里叶变换，得到如下结论：空间域中两个函数的卷积的傅里叶变换等于两个函数的傅里叶变换在频率域中的乘积。

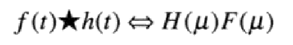
       H(u)是h(u)的傅里叶变换，F(u)是f(u)的傅里叶变换，t所在的域为空间域，u所在的域为频率域。

       双箭头用于表示右边的表达式是通过对左边的表达式 执行傅里叶变换得到的；而左边的表达式是通过求右边的表达式的傅里叶反变换得到的。

       同理，频率域的卷积和空间域的乘积也是同样的关系：

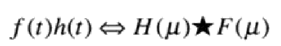
四． 取样和取样函数的傅里叶变换

（一） 取样

       计算机处理连续函数，需要转换为离散值序列，可以通过取样来完成。

       取样可以通过单位间隔的冲激串来作为取样函数乘以f(t)。

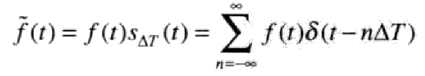
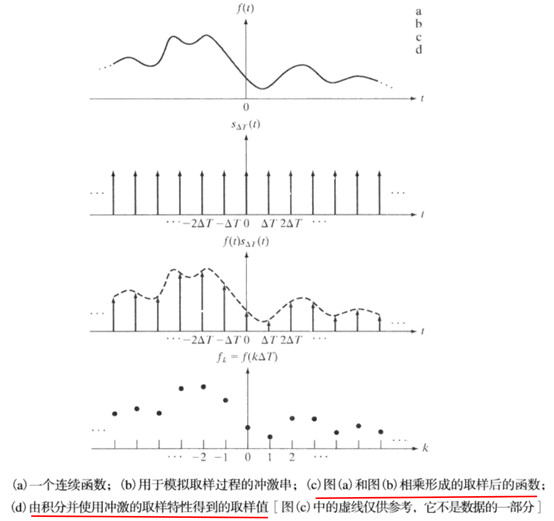
       取样的过程如下图所示：

（二） 取样函数的傅里叶变换

       由于取样后的函数是原始函数和冲激串的乘积，根据卷积定理得知，空间域两个函数乘积的傅里叶变换是两个函数在频率域的卷积。那么，取样函数的傅里叶变换就是两个函数在频率域的卷积。

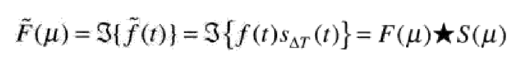
       冲激串的傅里叶变换：

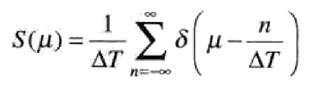
       于是得到取样后的函数的傅里叶变换为：

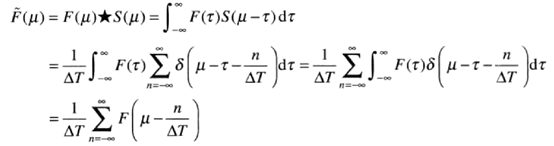
       可以看出，取样后的函数的傅里叶变换是F(u)的一个拷贝的无限周期序列，也是原始连续函数的傅里叶变换。拷贝间的间隔有 1 / △T的值决定。较高的1 / △T值在会使周期之间有更为清晰的间隔；而较低的 1 / △T值将会使周期之间融合。

（三） 取样定理

       一个连续函数完全可以由其取样集合恢复。

1. 带限函数

       对于以原点为中心的有限区间[-umax, umax]之外的频率值，其傅里叶变换为0的函数f(t)称为带限函数。

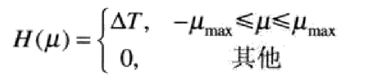
2. 恢复f(t)

       如果能从取样函数的傅里叶变换这个周期序列中分离出F(u)的一个拷贝，就可以通过傅里叶反变换恢复出f(t)。

       因此，我们需要使1 / △T的值足够大，提取出一个单周期。

       即要满足以下公式：

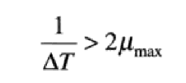
       该公式表明：如果以超过函数最高频率的两倍的取样率来取样本，连续的带限函数可以从它的样本集中恢复。这就是取样定理。

3. 函数复原完整过程

       带限函数H(u):（该带限函数又称为低通滤波器，因为它通过频率范围低端的频率）

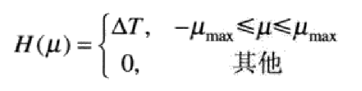
       将H(u)乘以取样后的函数得到F(u)

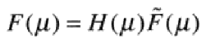
       通过傅里叶反变换复原f(t)：

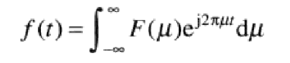
最后

以上就是虚拟麦片为你收集整理的【数字图像处理笔记（七）】之冲激和取样的傅里叶变换的全部内容，希望文章能够帮你解决【数字图像处理笔记（七）】之冲激和取样的傅里叶变换所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。