基于Matlab的汉明码纠错传输以及交织编码仿真
- 前言
- 原理
- 汉明码
- 编码过程
- 冗余位数量计算
- 校验位位置计算
- 计算校验相关位
- 开始编码
- 解码过程
- 实验结果
- 仿真代码
- 可以修改的参数
- 下载链接
- 主函数
- 汉明码编解码测试模块
- 汉明码编码器
- 汉明码解码器
- 冗余位计算模块
- 交织编码器
- 交织解码器
- 随机误码模块
- 比较模块
- 单极性码生成模块
- 随机码转单极性码模块
- 后语
前言
在上一篇文章《8位16位64位等任意数量用户CDMA直接序列扩频通信系统的Matlab仿真》中,介绍了一种多用户CDMA传输模型,但该模型存在一个缺陷,那就是无论信噪比多高,误码率始终无法为0,为了引入纠错码从而解决这个缺陷,在空闲时间研究了汉明码与交织编码技术,做出了Matlab模型,整理成文章给大家参考。
原理
汉明码
代码中编码与解码均采用奇校验。
编码过程
冗余位数量计算
∀
x
⊂
Z
+
且满足
2
x
≥
x
+
m
+
1
,
i
=
m
i
n
(
x
)
forall x subset Z^+且满足2^x geq x+m+1,i = min(x)
∀x⊂Z+且满足2x≥x+m+1,i=min(x)
其中,m为每一帧数据的二进制位数,i为冗余位数量。
校验位位置计算
校验位位置都出现在2的幂次方位,所以根据冗余位数量计算即可。如果冗余位数量为4,则校验位位置就是[1,2,4,8],注意,以上位置对应数组索引从一开始,即1表示第一位。
计算校验相关位
汉明码就是奇偶校验的升级版,它在编码结果中加入冗余位数量个奇偶校验位。每一个校验位都有不同的校验相关位,第一位校验位,它就跟索引在二进制下第一位是1的所有数据位有关。
假设传输的数据7位一帧,那么它的冗余位数量就是4,第一个冗余位出现在编码后的第一位,这一位要与[3 5 7 9 11]这些位做奇偶校验。
第2位校验位则跟索引在二进制第2位是1的所有数据进行奇偶校验;
。。。
第k位校验位则跟索引在二进制第k位是1的所有数据进行奇偶校验。
代码中用了按位与的方法,把每一个校验位对应的多个相关位找出来。
开始编码
对于每一帧数据,首先把用户的数据填入到编码结果的非校验位,然后对每个校验位及其校验相关位做奇校验,把校验结果填入校验位,即完成一帧的编码。
例如传输的数据7位一帧,那么它的冗余位数量就是4,冗余位序号,索引以及校验相关位如下图所示:
| 冗余位序号 | 冗余位位置索引 | 校验相关位索引 |
|---|---|---|
| 1 | 1 | 1 3 5 7 9 11 |
| 2 | 2 | 2 3 6 7 10 11 |
| 3 | 4 | 4 5 6 7 |
| 4 | 8 | 8 9 10 11 |
| 注意,以上索引指编码后的索引,且从1开始。 | ||
| 比如说用户需要发送:1011001,那么初步编码结果即为100?110?1??,?号表示冗余校验位。 | ||
| 把下表中的初步编码与第一冗余相关位进行逻辑与,带?号的位忽略,第一逻辑与结果中有4个1,所以冗余位应该填入1,使其满足奇校验,接着把第二冗余相关位与初步编码进行逻辑与,重复上述步骤,以此类推,即可得到每个冗余位的值。 | ||
| 位序号 | 11 | 10 |
| -------- | ----- | -------- |
| 初步编码 | 1 | 0 |
| 第一冗余相关位 | 1 | 0 |
| 第一逻辑与结果 | 1 | 0 |
| 第一冗余结果 | 0 | 0 |
| 位序号 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 第二初步编码 | 1 | 0 | 1 | ? | 1 | 0 | 0 | ? | 1 | ? | 1 |
| 第二冗余相关位 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 第二逻辑与结果 | 1 | 0 | 0 | ? | 1 | 0 | 0 | ? | 1 | ? | 0 |
| 第二冗余结果 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ?=0 | 0 |
| 位序号 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 第三初步编码 | 1 | 0 | 1 | ? | 1 | 0 | 0 | ? | 1 | 0 | 1 |
| 第三冗余相关位 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 第三逻辑与结果 | 0 | 0 | 0 | ? | 1 | 0 | 0 | ? | 0 | 0 | 0 |
| 第三冗余结果 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ?=0 | 0 | 0 | 0 |
| 位序号 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 第四初步编码 | 1 | 0 | 1 | ? | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 第四冗余相关位 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 第四逻辑与结果 | 1 | 0 | 1 | ? | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 第四冗余结果 | 0 | 0 | 0 | ?=1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 位序号 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 编码结果 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
解码过程
解码同样要计算校验位位置与校验相关位,然后对每一个校验位及其校验相关位进行奇校验,校验正确输出0,校验失败输出1。仍是上面的例子,假设接收端接收时出错,上面的编码结果:10111000101的第6位变成了1,即接收到了:10111100101,接收端的解码过程如下:
把接受结果依次与四种冗余相关位进行逻辑与,然后分别统计结果中”1“的个数是否为奇数个,是则输出0,否则输出1。
| 位序号 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 接收结果 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 第一冗余相关位 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 第一逻辑与结果 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 第一逻辑与结果有5个”1“,输出0,奇校验通过。 | |||||||||||
| 位序号 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| -------- | ----- | -------- | ----- | -------- | ----- | -------- | ----- | -------- | ----- | — | — |
| 接收结果 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 第二冗余相关位 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 第二逻辑与结果 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 第二逻辑与结果有4个”1“,奇校验失败,输出1 | |||||||||||
| 位序号 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| -------- | ----- | -------- | ----- | -------- | ----- | -------- | ----- | -------- | ----- | — | — |
| 接收结果 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 第三冗余相关位 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 第三逻辑与结果 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 第三逻辑与结果有2个”1“,奇校验失败,输出1 | |||||||||||
| 位序号 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| -------- | ----- | -------- | ----- | -------- | ----- | -------- | ----- | -------- | ----- | — | — |
| 接收结果 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 第四冗余相关位 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 第四逻辑与结果 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 第四逻辑与结果有3个”1“,输出0,奇校验通过。 | |||||||||||
| 把以上的输出从第四到第一进行排列,可得0110,这是6的二进制,标志着第6位传输出错!因为传输的是二进制,只要对第六位取反,就可以得到发送的码元。 | |||||||||||
| 以上就是汉明码纠错原理,它可以纠正一帧中的一维错码,对于多位错码的情况,可以使用更复杂的BCH编码,此处不再介绍。 |
实验结果
实验参数:
- 汉明编码一帧对应8个用户码元
- 交织编码一帧对应16个用户码元
- 用户码元数设置为1e5 * 8个
- 信道误码率范围:10^(-4) 到10^(-0.3)
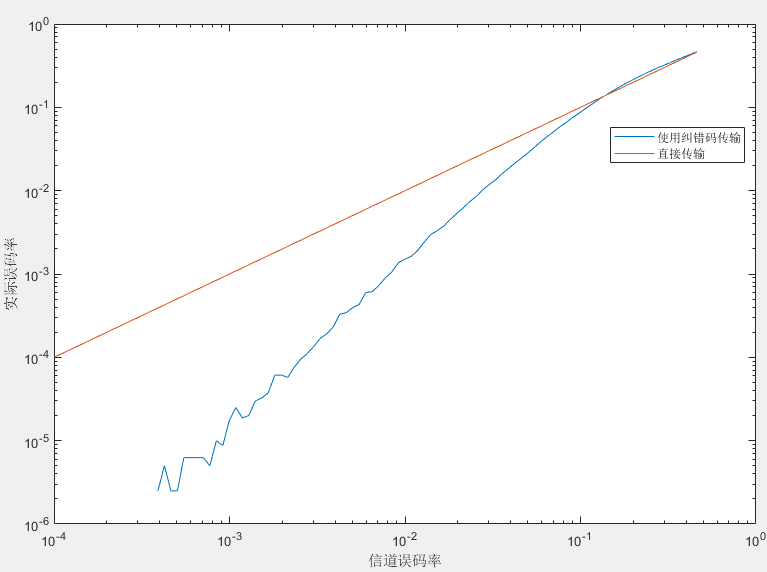
实验结果显示,在信道误码率小于0.128时,使用纠错编码传输对于通信质量有显著改善,甚至在信道误码率小于4e-4时,可以0误码传输,在信道误码率大于0.128时,使用纠错码无实际意义。
仿真代码
可以修改的参数
- 汉明编码一帧的码元数
- 交织编码一帧的码元数
- 测试的码元数量
- 误码率开始数
- 误码率结束数
- 误码率尝试数
下载链接
GitHub: https://github.com/highskyno1/hamming_en-decode
度盘:https://pan.baidu.com/s/13YSblZQoAWjCibgU7Mtmmw
提取码:jrgi
主函数
main.m
%{
本代码实现了对用户二进制码元的纠错编码与解码。
核心功能采用的汉明码的方法。
2020/8/4 23:10
加入了交织编码技术,一定程度上避免了突发连续错误带来的误码
2020/8/5 11:19
%}
%汉明编码一帧的码元数,对数据冗余度有影响
hamming_frame_size = 8;
%交织编码一帧的码元数,越大对于抵抗突发连续错误越好,但会增加处理时延
mixed_frame_size = 16;
%测试的码元数量,必须是frame_size以及mixed_frame_size的整数倍
code_num = 1e5 * 8;
%生成用户码元
user_code = genBipolar(code_num);
%交织编码
mix_code = mixed_encode(user_code,mixed_frame_size);
%发送出去的编码后的码元
send_code = hamming_encode(mix_code,hamming_frame_size);
fprintf('冗余度:%fn',length(send_code)/length(user_code));
%误码率开始数
error_start = -4; % -4指10^-4
%误码率结束数
error_end = -0.3; % -0.3指10^(-0.3)
%误码率尝试数
error_size = 100;
%记录信道误码率的数组
channel_error_rec = zeros(1,error_size);
%记录实际误码率的数组
error_rec = zeros(1,error_size);
parfor error_index = 1:error_size
%当前信道误码率
error_rate = 10^(error_start + (error_index-1) / error_size * (error_end - error_start));
channel_error_rec(error_index) = error_rate;
%随机误码
rec_code = randErrorCode(send_code,error_rate);
%解码后的码元
de_code = hamming_decode(rec_code,hamming_frame_size);
%交织解码
res_code = mixed_decode(de_code,mixed_frame_size);
%计算实际误码率
[~,accuracy] = compare(user_code,res_code);
error_rec(error_index) = 1 - accuracy;
fprintf('信道误码率:%f,实际误码率:%fn',error_rate,1-accuracy);
end
%绘制实际误码率与信道误码率关系图
figure();
loglog(channel_error_rec,error_rec);
hold on;
loglog(channel_error_rec,channel_error_rec);
xlabel('信道误码率');
ylabel('实际误码率');
legend('使用纠错码传输','直接传输');
汉明码编解码测试模块
hamming_test.m
user_code = [1 0 0 1 1 0 1];
en_code = encode(user_code,7);
%误码位
en_code(11) = ~en_code(11);
de_code = decode(en_code,7);
%计算正确率
[~,accuracy] = compare(user_code,de_code);
fprintf('误码率:%fn',1-accuracy);
汉明码编码器
hamming_encode.m
function res = hamming_encode(input,frame_size)
%encode 对输入的二进制数组进行汉明码编码,奇校验
%input:需要编码的二进制数组
%frame_size:每一帧数据的二进制位数
len_input = length(input);
if mod(len_input,frame_size) ~= 0
error('输入的数组数必须是分组数的整数倍')
end
%计算冗余位数量
red_bit_num = red_bit_cal(frame_size);
%总的位数
bit_num = red_bit_num + frame_size;
%帧数量
frame_num = len_input / frame_size;
%计算校验位的位置
pos_red_bit = 2.^(0:red_bit_num-1);
%计算校验位的相关位
pos_relat_bit = uint8(zeros(red_bit_num,bit_num));
for i = 1:red_bit_num
for j = 1:bit_num
if bitand(2^(i-1),j) ~= 0
pos_relat_bit(i,j) = 1;
end
end
end
%初始化一个结果单元
res = uint8(zeros(frame_num,bit_num));
%填满每一帧的数据位
index = 1;
for i = 1:frame_num
for j = 1:bit_num
if ismember(j,pos_red_bit)
continue
end
res(i,j) = input(index);
index = index + 1;
end
end
%对每一帧加入校验位
for i = 1:frame_num
for j = 1:red_bit_num
foo = bitand(res(i,:),pos_relat_bit(j,:));
foo = mod(sum(foo)+1,2);
res(i,pos_red_bit(j)) = foo;
end
end
res = res';
res = res(:);
end
汉明码解码器
hamming_decode.m
function res = hamming_decode(input,frame_size)
%decode 对输入的二进制数组进行汉明码解码,奇校验
%input:需要编码的二进制数组
%frame_size:每一帧数据的二进制位数
len_input = length(input);
%计算冗余位数量
red_bit_num = red_bit_cal(frame_size);
%总的位数
bit_num = red_bit_num + frame_size;
if mod(len_input,bit_num) ~= 0
error('输入的数组数必须是总的位数的整数倍');
end
%帧数量
frame_num = len_input / bit_num;
%对输入进行重构
input = uint8(input);
input = reshape(input,bit_num,frame_num);
input = input';
%计算校验位的位置
pos_red_bit = 2.^(0:red_bit_num-1);
%计算校验位的相关位
pos_relat_bit = uint8(zeros(red_bit_num,bit_num));
for i = 1:red_bit_num
for j = 1:bit_num
if bitand(2^(i-1),j) ~= 0
pos_relat_bit(i,j) = 1;
end
end
end
%开始校验,注意是奇校验
for i = 1:frame_num
%该帧的校验结果
res_verify = uint8(zeros(1,red_bit_num));
for j = 1:red_bit_num
foo = sum(bitand(input(i,:),pos_relat_bit(j,:)));
if mod(foo,2) == 0
%奇校验失败
res_verify(j) = 1;
end
end
%计算出错位
%转换为小端序
res_verify = fliplr(res_verify);
error_bit_pos = 0;
for j = 1:red_bit_num
error_bit_pos = error_bit_pos*2 + res_verify(j);
end
%出错位取反
if error_bit_pos <= bit_num && error_bit_pos ~=0
%如果为0,则没有发生传输错误
input(i,error_bit_pos) = ~input(i,error_bit_pos);
end
end
%提取结果
res = uint8(zeros(1,frame_num*frame_size));
res_index = 1;
for i = 1:frame_num
for j = 1:bit_num
if ismember(j,pos_red_bit)
continue
end
res(res_index) = input(i,j);
res_index = res_index + 1;
end
end
end
冗余位计算模块
red_bit_cal.m
function res = red_bit_cal(group_num)
%red_bit_cal 计算冗余位数量
%group_num:每一帧数据的二进制位数
res = 0;
while 2^res - res < group_num + 1
res = res + 1;
end
end
交织编码器
mixed_encode.m
function res = mixed_encode(input,frame_size)
%mined_encode 本函数用于对输入信号进行交织编码
%input:用户数据
%frame_size:一帧数据所包含的二进制码元数
len_input = length(input);
if mod(len_input,frame_size) ~= 0
error('用户数据二进制数必须为帧数的整数倍');
end
frame_num = len_input / frame_size;
res = reshape(input,frame_num,frame_size);
res = res';
res = res(:);
end
交织解码器
mixed_decode.m
function res = mixed_decode(input,frame_size)
%mined_encode 本函数用于对输入信号进行交织解码
%input:用户数据
%frame_size:一帧数据所包含的二进制码元数
len_input = length(input);
if mod(len_input,frame_size) ~= 0
error('用户数据二进制数必须为帧数的整数倍');
end
frame_num = len_input / frame_size;
res = reshape(input,frame_size,frame_num);
res = res';
res = res(:);
end
随机误码模块
randErrorCode.m
function res = randErrorCode(input,error_rate)
%randErrorCode 对输入的码元数组添加随机误码
%input:数组
%error_rate:误码率(%)
res = input;
for i = 1:length(input)
if rand() < error_rate
res(i) = ~res(i);
end
end
end
比较模块
compare.m
%比较两个数组
%input1:数组1
%input2:数组2
%res:正确码元数量
%accuracy:正确率
function [res,accuracy] = compare(input1,input2)
len1 = length(input1);
len2 = length(input2);
len = min(len1,len2);
right_code = 0;
for i = 1:len
if input1(i) == input2(i)
right_code = right_code + 1;
end
end
res = right_code;
accuracy = right_code / len;
end
单极性码生成模块
genBipolar.m
%产生单极性码
%num:单极性码的规模
%res:满载单极性码的数组
function res = genBipolar(num)
res = rand(1,num);
res = value2Bipolar(res);
end
随机码转单极性码模块
value2Bipolar.m
% 本函数用户把随机生成的0~1之间的double数转换成双极性码
function res = value2Bipolar(input)
res = zeros(1,length(input));
for index = 1:length(input)
if(input(index) > 0.5)
res(index) = 1;
end
end
res = uint8(res);
end
后语
终于把纠错码模型做出来了,接下来可以去修改任意用户CDMA传输模型了。前几天趁着有空,去了张家界旅游,自由行,一共5天。那边空气非常清新,但是景区的设计非常坑爹,经常都是至少坐一次缆车或者天梯,才能在景区下班前离开景区,但风景是真的不错。昨天收到通知,初步确定9月24号才能回到学校,这个暑假又延长了!
最后
以上就是孤独蜻蜓最近收集整理的关于【通信系统仿真系列】基于Matlab的汉明码(Hamming Code)纠错传输以及交织编码(Interleaved coding)仿真前言原理汉明码实验结果仿真代码后语的全部内容,更多相关【通信系统仿真系列】基于Matlab的汉明码(Hamming内容请搜索靠谱客的其他文章。








发表评论 取消回复