加窗函数后频谱幅值发生了变化的修正技巧

87 阅读 0 评论 58 点赞

我是靠谱客的博主粗心发卡，最近开发中收集的这篇文章主要介绍加窗函数后频谱幅值发生了变化的修正技巧，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

在加窗函数前、后计算的频谱幅值发生了变化（矩形窗除外），这个变化是怎么发生的？该如何修正幅值呢？下面以汉宁窗函数为例进行说明。

一、矩形窗函数和汉宁窗函数的频谱

先来说明矩形窗函数的频谱。设离散的矩形窗函数rN（n）为

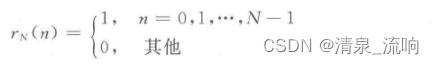
rN（n)的离散时间傅里叶变换（DTFT）为

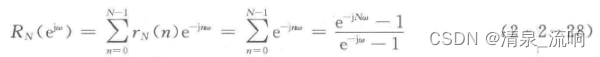
利用三角函数的关系，由式（2-2-28）可导出

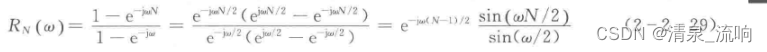
式（2-2-29）就是矩形窗函数DTFT的频谱。

设汉宁窗函数为

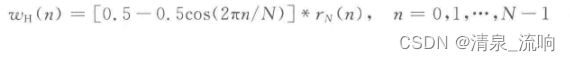
式中：rN（n)就是式（2-2-27)的矩形窗函数。由式（2-2-23)wH（n)的离散时间傅里叶变换
（DTFT）为

式中的Rv就是矩形窗函数的DTFT频谱，由式（2-2-29）表示；而式（2-2-31）给出了汉宁窗函数DTFT的频谱。

二、汉宁窗的幅值修正计算如下：
设修正系数为K，定义为

式中：AR为矩形窗的幅值，AH为汉宁窗的幅值。把式（2-2-29）与式（2-2-31）相除，令w=
0,有

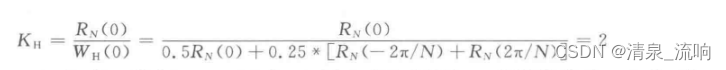
将上式中w=2π/N代人到式（2-2-29）中，RN（土2π/N）的值为0。所以得到KH=2，KH表示为汉宁窗的修正系数。
下面把一些主要窗函数的幅值恢复系数列，在下表中，表内MATLAB函数中的N是窗函数的长度。

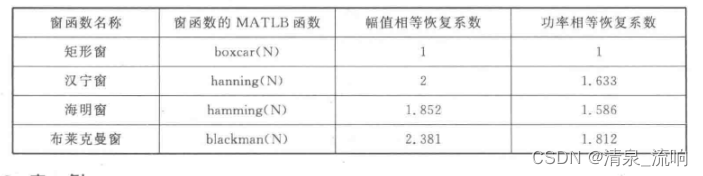
案例、信号由两个余弦信号组成，频率分别为f1=50Hz和f2=65.75Hz，幅值都为1，初始相角都为0，信号长度为1000，采样频率为1000Hz。通过加汉宁窗函数FFT求出两个正弦信号的幅值和初始相角。程序如下：

clear all; clc; close all;

fs=1000;                         % 采样频率
N=1000;                          % 信号长度
t=(0:N-1)/fs;                    % 设置时间序列
f1=50; f2=65.75;                 % 两信号频率
x=cos(2*pi*f1*t)+cos(2*pi*f2*t); % 设置信号
wind=hanning(N)';
X=fft(x.*wind);                  % 乘窗函数并FFT
Y=abs(X)*2/1000;                 % 计算幅值
freq=fs*(0:N/2)/1000;            % 设置频率刻度
[A1, k1]=max(Y(45:65));          % 寻求第1个信号的幅值
k1=k1+44;                        % 修正索引号
[A2, k2]=max(Y(60:70));          % 寻求第1个信号的幅值
k2=k2+59;                        % 修正索引号
Theta1=angle(X(k1));             % 计算信号f1的初始相角
Theta2=angle(X(k2));             % 计算信号f2的初始相角
Y1=Y*2;                          % 对加窗后的幅值进行修正
% 显示频率和幅值
fprintf('f1=%5.2f   A1=%5.4f   A11=%5.4f   Theta1=%5.4fn',freq(k1),A1,A1*2,Theta1); 
fprintf('f2=%5.2f   A2=%5.4f   A21=%5.4f   Theta2=%5.4fn',freq(k2),A2,A2*2,Theta2);

% 作图
subplot 211; plot(freq,Y(1:N/2+1),'k'); xlim([40 75]); 
line([0 100],[.5 .5],'color','k');
xlabel('频率/Hz'); ylabel('幅值'); title('(a)频谱图-幅值修正前');
subplot 212; plot(freq,Y1(1:N/2+1),'k'); xlim([40 75]); 
line([0 100],[1 1],'color','k');
xlabel('频率/Hz'); ylabel('幅值'); title('(b)频谱图-幅值修正后');
set(gcf,'color','w');

运行结果如下：

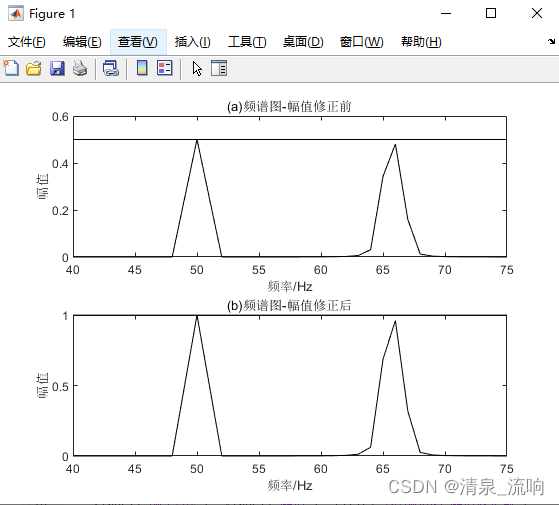
其中f1和f2表示两信号的频率，A1和A2表示两信号修正前的幅值，A11和A21表示两信号修正后的幅值，Theta1和Theta2表示两信号的初始相位角。而第1个信号的幅值和初始相角非常接近
于设置值，误差比例2-2-2的结果有很大的改善（例2-2-2中求得信号f1的幅值为A1=0.9896，初始相角为Thetal=0.0089）。这说明两个问题：①在例2-2-2中幅值和初始相角产生的误差是由第2个信号的泄漏造成的；②加了窗函数以后能减小泄漏，但幅值还是有些误差，若使用泄漏更小的窗函数则可进一步提高幅值的精度。

参考文献：MATLAB数字信号处理85个实用案例精讲——入门到进阶；宋知用（编著）