使用比值校正法消除信号中正弦信号的干扰

103 阅读 0 评论 68 点赞

我是靠谱客的博主无限大侠，最近开发中收集的这篇文章主要介绍使用比值校正法消除信号中正弦信号的干扰，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

在实际测量的信号中常常会混有正弦信号，有时不只含有一个正弦信号基波分量，而是一个畸变了的正弦信号，其中包含复杂的频率成分，即包含了基波和它的各次谐波。要消除这些基波和谐波当然可以用滤波的方法来清除，但如果基波外还有2～99次的谐波，那么要清除起来就不是那么轻松了。下面的例子就是包含有基波和2~99次的谐波，采用了类似于滤波的方法，但不是用滤波器来消除畸变了的正弦信号。

对于一个离散的正弦信号x（n），可以表示为x(n)=Acos(2π*f0*t＋φ0)
其中：A是正弦信号x（n)的幅值，f0和φ0是x（n)的频率和初始相角，它们是正弦信号的三个要素。因此在已知采样频率fs的条件下，一旦这三个要素A、f0和φ0决定下来，则这个正弦信号就可以完整地被仿真出来，可以求出任何时刻x（n）的值。若利用比值校正方法求出正弦信号的三个要素，设为A'、f0'和φ0'，仿真出信号y（n）为y(n)=A'cos(2π*f0'*t+φ0')

则它们的差值e（n)=x（n)一y（n）。只要校正方法计算得到的A'、f0'和φ0'十分接近于A、f0
和φ0，那么e（n）就是消除该正弦信号后的信号。我们用这种方法来消除正弦信号的干扰（不
用滤波器的“滤波”），该方法的优点是不用滤波器，不会有滤波器造成的影响（包括信号的延
迟、信号的瞬态响应等），缺点是消噪的程度取决于校正方法达到的精度。同时这种方法不限于用比值校正法，但其他校正法一样适用，只要能求出正弦信号的三个要素，就能用本方法对正弦信号进行“滤波”。

比值校正法函数如下：

名称：specor_ml
功能：用矩形窗和汉宁窗进行比值法校正，计算出正弦信号的频率、幅值和初始相角
调用格式：

Z= specor_m1(x,fs,N,NX,method)
说明：本函数是参照振动论坛上yangzj提供的程序修改而来的。函数的输入参数x是被测的信号序列，fs是采样频率，N是FFT的长度（默认值是x的长度），NX是寻找峰值的频率区间，给的是频率值（默认值是[0 fs/2]），method是说明用矩形窗（method=1）或用汉宁窗（method=2）（默认值是method=1）。输出参数Z有3个元素，Z（1）是正弦信号的频率，Z（2）是信号的幅值，Z（3）是信号的初始幅值（在-pi~pi之间）。因为在信号中可能有许多峰值，为了求一个特定的峰值，则先设置求该峰值的频率区间NX。函数程序如下：

function Z=specor_m1(x,fs,N,NX,method)
if nargin<3, N=length(x); NX=[0 fs/2]; method=1; end % 参数不足时的设置
if nargin<4, NX=[0 fs/2]; method=1; end
if nargin<5, method=1; end
if method<1 | method>2           % method小于1或大于2,都设为method=1
    disp('method-value should be equal to 1 or 2');
    method=1;
end
x=x(:)';                         % 设置x为行序列
w=hann(N,'periodic');            % 求出海宁窗函数
if method==2                     % 若调用时用海宁窗函数
    xf=fft(x.*w');               % 信号加窗后FFT
    xf=xf(1:N/2)/N*4;            % 把信号的幅值修正
    WindowType=2;                % 设WindowType=2;
else
    xf=fft(x);                   % FFT
    xf=xf(1:N/2)/N*2;            % 把信号的幅值修正
    WindowType=1;                % 设WindowType=1;
end
ddf=fs/N;                        % 求出频率分辨率
nx1=NX(1); nx2=NX(2);            % 给出求最大值频率的区间
n1=fix(nx1/ddf);                 % 按频率区间给出索引号
n2=round(nx2/ddf);

A=abs(xf);                       % 求取模值
[Amax,index]=max(A(n1:n2));      % 从索引号取间求出最大值
index=index+n1-1;                % 给出最大值的索引号
phmax=angle(xf(index));          % 求出相角未修正时的数值
    
%比值法_加矩形窗
if (WindowType==1)               % 若是矩形窗
    indsecL=A(index-1)>A(index+1);  % 给出X(k-1)>X(k+1)的逻辑量
    % 按式(6-2-5)计算Δk
    df=indsecL.*A(index-1)./(Amax+A(index-1))-...
        (1-indsecL).*A(index+1)./(Amax+A(index+1));
    Z(1)=(index-1-df)*ddf;       % 按式(6-2-6)计算频率
    Z(2)=Amax/sinc(df);          % 按式(6-2-8)计算幅值
    Z(3)=phmax+pi*df;            % 按式(6-2-12)计算初始相角
end
    
%比值法_加Hanning窗
if (WindowType==2)               % 若是海宁窗
    indsecL=A(index-1)>A(index+1);  % 给出X(k-1)>X(k+1)的逻辑量
    % 按式(6-2-29)计算Δk
    df=indsecL.*(2*A(index-1)-Amax)./(Amax+A(index-1))-...
        (1-indsecL).*(2*A(index+1)-Amax)./(Amax+A(index+1));
    Z(1)=(index-1-df)*ddf;       % 按式(6-2-6)计算频率
    Z(2)=(1-df^2)*Amax/sinc(df); % 按式(6-2-31)计算幅值
    Z(3)=phmax+pi*df;            % 按式(6-2-12)计算初始相角
end
Z(3)=mod(Z(3),2*pi);             % 以保证初始相角在-pi~pi的区间中
Z(3)=Z(3)-(Z(3)>pi)*2*pi+(Z(3)<-pi)*2*pi;

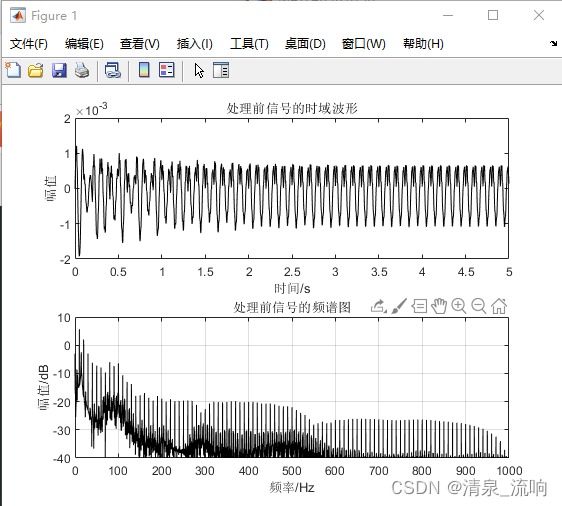
案例、实测得到一个系统的脉冲响应(在文件uy_25a.txt中),但在该脉冲响应中混有畸变了的正弦信号，该正弦信号几乎淹没了实际信号。希望通过消除这些正弦信号恢复出系统实际的脉冲响应信号。先进行频谱分析，可以看到这系统的脉冲响应信号中混有10Hz的基波和它的谐波，谐波的阶数差不多由2至99阶。所以通过比值校正法估算基波和每一阶谐波的参数，然后仿真它们，从原始信号中减去仿真值，以达到消除干扰的目的。程序如下：

clear all; clc; close all;

xx=load('uy_25a.txt');                 % 读入数据文件
t=xx(:,1); x=xx(:,2);                  % 得到时间序列和信号序列
dt=t(2)-t(1); fs=1/dt;                 % 求出采样频率
N=length(x);                           % 数据长度
y=x;                                   % 保存原始信号在y中
n=1:N; n2=1:N/2+1;                     % 设置n和n2
df=fs/N;                               % 给出频率分辨率
freq=(n2-1)*df;                        % 给出频率刻度
Y=fft(y);                              % 给出原始信号的频谱

rad=pi/180;                            % 1弧度值
DX=[5 15];                             % 寻找基波的区间
t=(0:N-1)/fs;                          % 设置时间刻度
for k=1 : 99                           % 求基波及2~99阶谐波的参数
    if k==1                           % 当k为1,即求基波参数
        NX=DX;                         % 给出寻找基波的区间
        Z=specor_m1(x,fs,N,NX,2);      % 比值校正法求出基波的参数
        u=Z(2)*cos(2*pi*Z(1)*t+Z(3));  % 仿真出基波信号
        x=x'-u;                        % 从原始信号中减去基波的成分
        f0=Z(1);                       % 基波的频率
    else                               % 求2~99阶谐波的参数
        NX=[k*f0-DX(1) k*f0+DX(1)];    % 给出寻找k阶谐波的频率区间
        Z=specor_m1(x,fs,N,NX,2);      % 比值校正法求出k阶谐波的参数
        u=Z(2)*cos(2*pi*Z(1)*t+Z(3));  % 仿真出k阶谐波信号
        x=x-u;                         % 从原始信号中减去k阶谐波的成分
    end
end
X=fft(x);                              % 消除正弦信号后的频谱
% 作图
figure(1);
subplot 211; plot(t,y,'k')
axis([0 5 -2e-3 2e-3]); title('处理前信号的时域波形');
xlabel('时间/s'); ylabel('幅值');
subplot 212; plot(freq,10*log10(abs(Y(n2))),'k');  
axis([0 1000 -40 10]); title('处理前信号的频谱图');
xlabel('频率/Hz'); ylabel('幅值/dB'); grid;
set(gcf,'color','w'); 

figure(2);
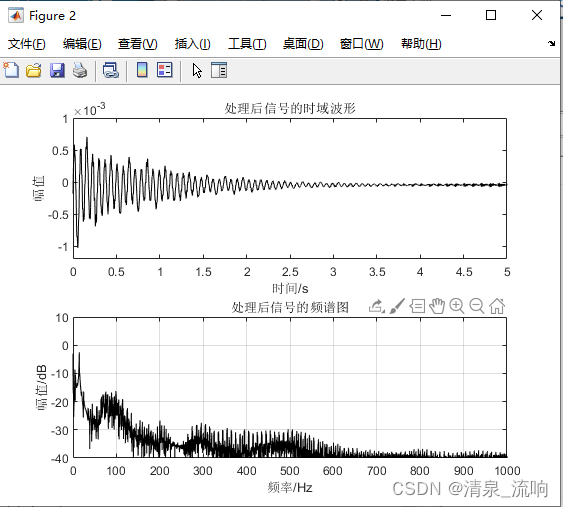
subplot 211; plot(t,x,'k')
axis([0 5 -1.2e-3 1e-3]); title('处理后信号的时域波形');
xlabel('时间/s'); ylabel('幅值');
subplot 212; plot(freq,10*log10(abs(X(n2))),'k'); 
axis([0 1000 -40 10]); title('处理后信号的频谱图');
xlabel('频率/Hz'); ylabel('幅值/dB'); grid;
set(gcf,'color','w');

运行结果如下：

说明：
①在程序中先求基波的频率，从频谱分析知道基波频率的大致区间，设置了寻找基波的频率区间DX=[5 15]。在求出基波后设置基波频率为f0。
②在求谐波时由于谐波频率不一定是基波的整数倍，而是在整数倍附近，所以对第k次谐波一样给出寻找频率的区间，设为XN=[k*f0-5 k*f0+5]。
③不论求出基波或谐波的参数后，都构成仿真的信号u=Z（2）*cos（2*pi*Z（1）*t+Z（3）），并从原始信号中减去：x=x-u。
④用汉宁窗能达到较高的精度，所以在本程序中都用汉宁窗的比值校正。

用本方法不能完全把正弦信号消除，因为用校正方法得到正弦信号的参数只是实际信号参数的一个近似值，有一个精度的限制。本章参考文献[4]中介绍比值法时，由于相角的精度为1°，相对误差约为1%，故采用仿真波形来消除正弦波的干扰，能把干扰衰减约40dB。

使用到的实验数据下载链接如下：

https://mp.csdn.net/mp_download/manage/download/UpDetailed

参考文献：MATLAB数字信号处理85个实用案例精讲——入门到进阶；宋知用（编著）