傅里叶变换与傅里叶级数

傅里叶级数

对于满足狄利克雷条件的周期信号可以进行傅里叶展开，对于周期函数f(t)，其周期为T1，角频率为w1 = 2π/T1,f1 = 1/T1，其傅里叶级数展开为：

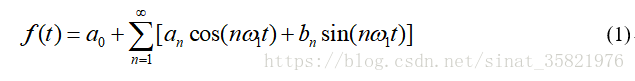
上式的右端就是所谓的傅里叶级数。周期信号按照傅里叶级数展开，可以分解成为直流分量a0，和许多正余弦分量an,bn而这些正余弦的分量必定是基频f1(1/T,T为周期函数的周期)的整数倍）。

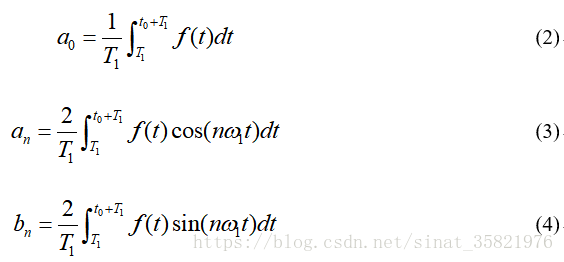
将（1）式相同的频率项合并，可以写成：

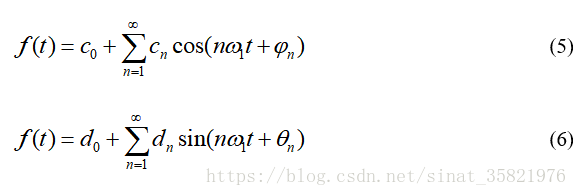
把cn或dn对nw1 的关系绘制成下图的曲线，得到的就是周期信号的幅度频谱，其中每一条线代表某一频率分量的的幅度。

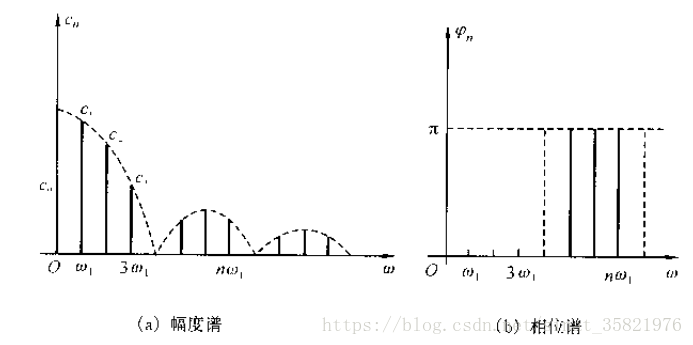
根据欧拉公式可以将傅里叶级数写成指数形式

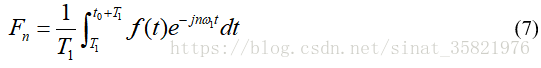
傅里叶变换

而对于非周期信号，可以视为周期无限大的周期信号，但当T1无限大时，w1 = 2π/T1间隔无限小，因此非周期信号的谱线就由离散变为连续，并且此时谱线长度Fn趋于0，则按照周期信号计算的频谱化为乌有。但是从物理上来说信号存在，那么必定有相应的能量存在，因此为了解决这个问题引入了频谱密度函数从傅里叶级数导出傅里叶变换。具体推导过程本文就不详讲，直接给出傅里叶变换的公式：

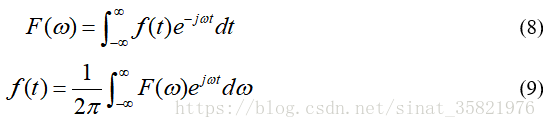
傅里叶变换又分离散和非离散，这里给出一个总结

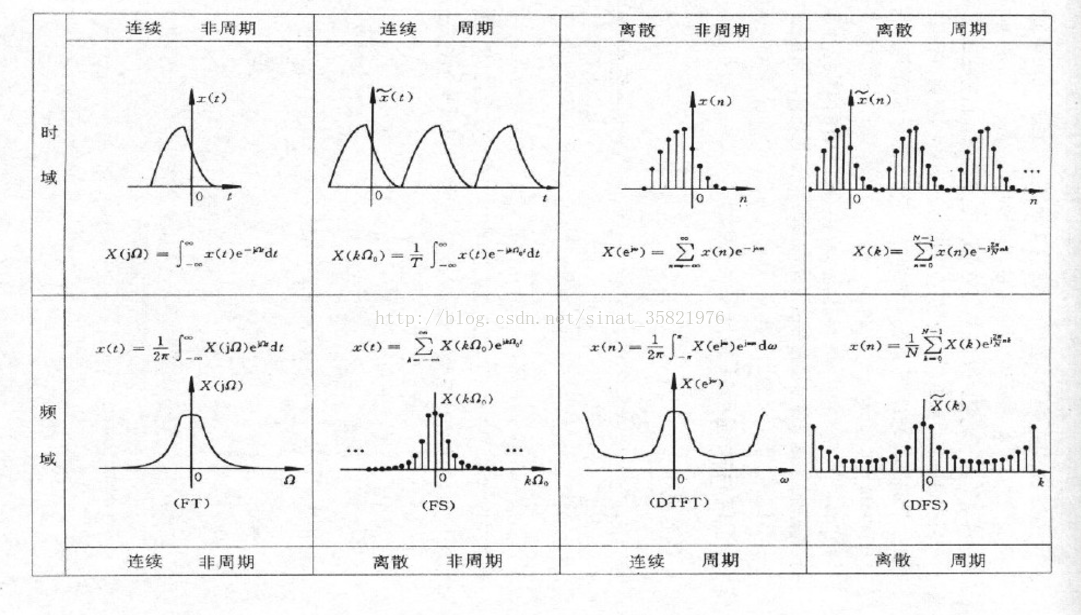
傅里叶变换与频谱、功率谱、能量

在上文讲到，一个信号可以分解成无数个周期信号的叠加，每个信号都有自己的频率分量，描述这种频率分量的图叫做频谱图。频谱图分为两部分，一部分是幅度频谱，另一部分是相位谱。语音中不怎么关注相位，因此下面会多讲一下幅度谱。任意信号经过傅里叶变换（FFT）可到的是一个复数序列，每一项记为a+ib。以下面代码为例

fs = 1000;            % 采样频率                   
T = 1/fs;             % 采样周期       
L = 1500;             % 信号长度
t = (0:L-1)*T;        % 时间
S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
signal = S + 2*randn(size(t));
figure;
plot(1000*t(1:50),signal(1:50))
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('t (milliseconds)')
ylabel('X(t)')
Y = fft(signal);
L = length(signal);
P2 = abs(Y/L);    %频谱
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);    
%P1 = 20*log10(P1); 
f = fs*(0:(L/2))/L;
figure;
plot(f,P1) ;
title('Single-Sided Amplitude Spectrum of X(t)');
xlabel('f (Hz)');
ylabel('|P1(f)|');

运行后我们可以看到，其中各个变量的类型与数目如上图所示。由于傅里叶变换后的点的个数与时域信号采样点个数相同（signal数组数目等于Y数组的数目），但是傅里叶变换是堆成的因此只用显示其中的一半即可（P1，一半会多取一点，这样不用考虑采样点的奇偶情况）。时域波形如下图所示

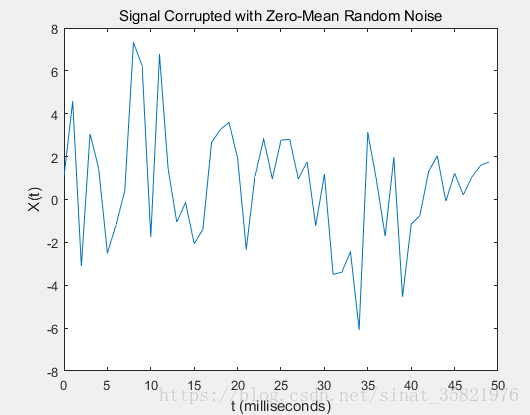
傅里叶变换得到复数的模即为频谱的幅值:

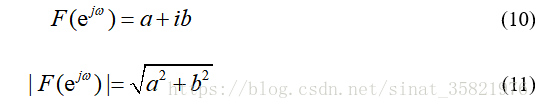
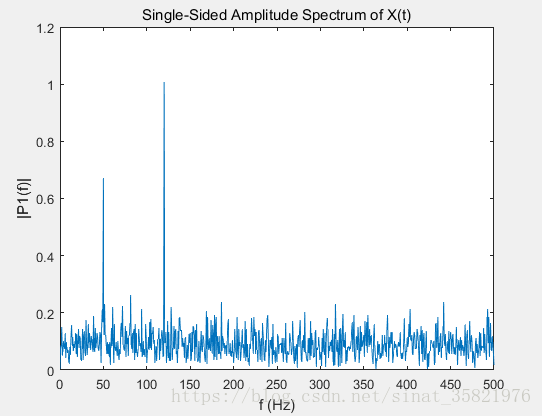
如下图所示，第一张图为单边频谱，第二张图为双边频谱

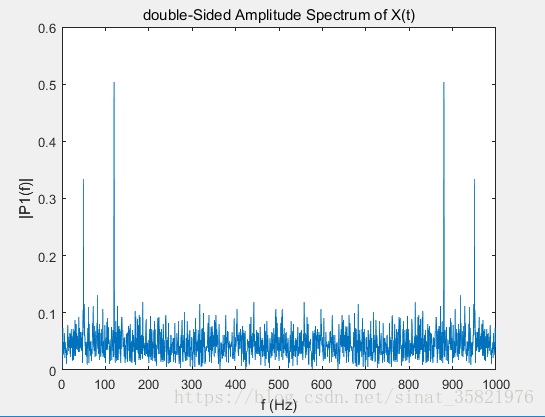
有时候也会用对数计算后的结果来表示频谱，此时单位为dB

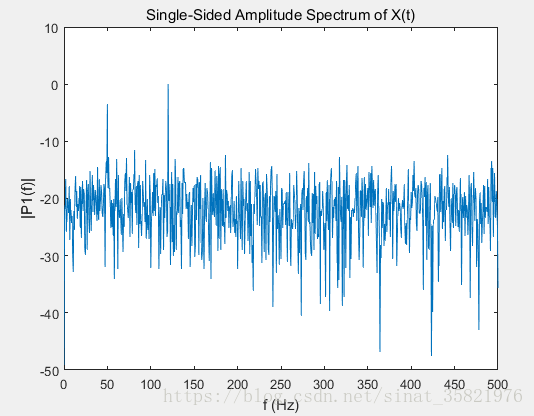
信号的能谱为信号频谱的平方，根据帕斯维尔定理，实信号的能量等于频域能量即

其中功率为

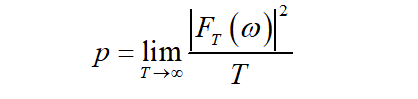
语音信号处理交流群：652292630

最后

以上就是勤劳春天为你收集整理的信号的傅里叶级数、傅里叶变换、频谱、功率谱、能量傅里叶变换与傅里叶级数傅里叶变换与频谱、功率谱、能量的全部内容，希望文章能够帮你解决信号的傅里叶级数、傅里叶变换、频谱、功率谱、能量傅里叶变换与傅里叶级数傅里叶变换与频谱、功率谱、能量所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。