文章目录
- 能量谱和功率谱
- 1 能量谱
- 1.1 信号能量
- 1.2. 帕斯瓦尔方程(能量方程)
- 1.3 能量密度谱E (ω)
- 2 功率谱
- 2.1 信号功率
- 2.2 功率密度谱
- 2.3 功率密度谱与自相关函数的关系
能量谱和功率谱
1 能量谱
1.1 信号能量
信号(电压或电流)
f
(
t
)
f(t)
f(t)在
1
Ω
1Ω
1Ω电阻上的瞬时功率为
∣
f
(
t
)
∣
2
|f(t)|^2
∣f(t)∣2,在区间
(
−
T
,
T
)
(-T, T)
(−T,T)的能量为
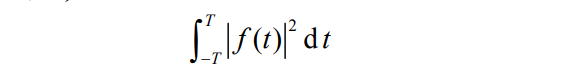
定义:时间
(
−
∞
,
∞
)
(-∞, ∞)
(−∞,∞)区间上信号的能量。
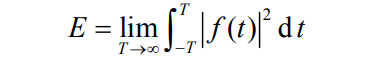
如果信号能量有限,即
0
<
E
<
∞
0<E<∞
0<E<∞,称为能量有限信号,简称能量信号。例如门函数,三角形脉冲,单边或双边指数衰减信号等
1.2. 帕斯瓦尔方程(能量方程)
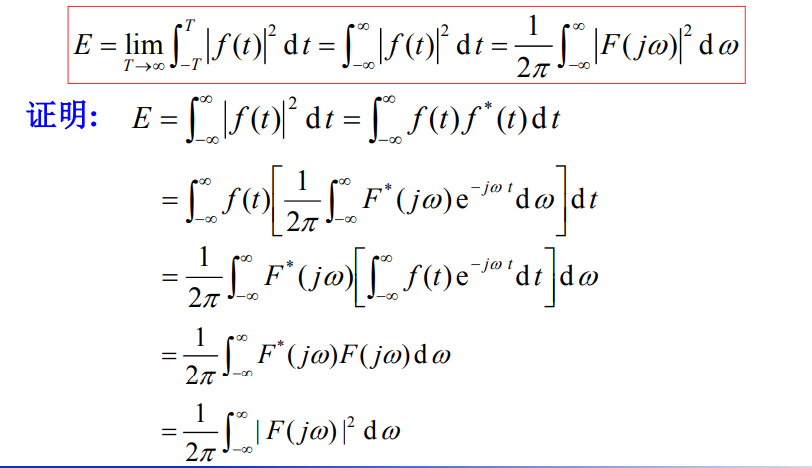
1.3 能量密度谱E (ω)
定义:单位频率的信号能量。
物理意义:为了表征能量在频域中的分布情况而定义的
能量密度函数,简称为能量频谱或能量谱。
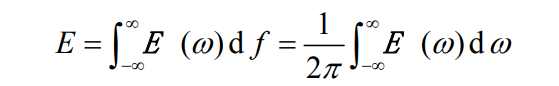
ω = 2 π f omega=2pi f ω=2πf
在频带 d f df df内信号的能量为 E ( ω ) d f E(ω) df E(ω)df,因而信号在整个频率区间 ( − ∞ , ∞ ) (-∞, ∞) (−∞,∞)的总能量为:
上式与帕斯瓦尔能量方程进行比较可知,
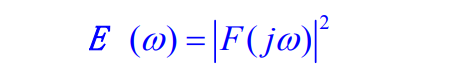
由相关定理:
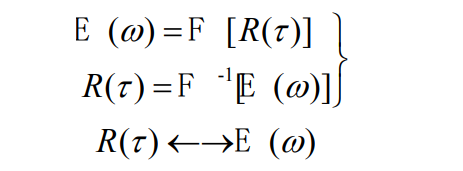
结论:能量有限信号的能量谱
E
(
ω
)
E (ω)
E(ω)与自相关函数
R
(
τ
)
R(τ)
R(τ)是一对傅里叶变换。

信号的能量谱
E
(
ω
)
E (ω)
E(ω) 是
ω
ω
ω的偶函数,它只取决于频谱函数的模量,而与相位无关。单位:
J
⋅
s
J·s
J⋅s。

2 功率谱
2.1 信号功率
定义:时间
(
−
∞
,
∞
)
(-∞, ∞)
(−∞,∞)区间上信号f(t)的平均功率。
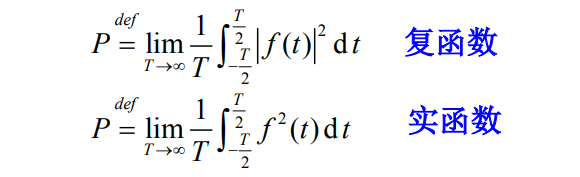
如果信号功率有限,即
0
<
P
<
∞
0<P<∞
0<P<∞,信号称为功率有限信号,简称功率信号。如周期信号等。
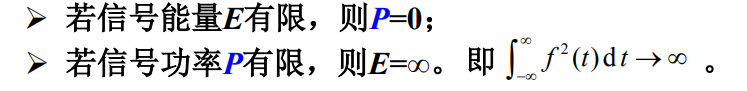
从
f
(
t
)
f(t)
f(t)中截取
∣
t
∣
≤
T
/
2
|t|≤T/2
∣t∣≤T/2的一段,得到一个截尾函数
f
T
(
t
)
f_T(t)
fT(t),它可以表示为:
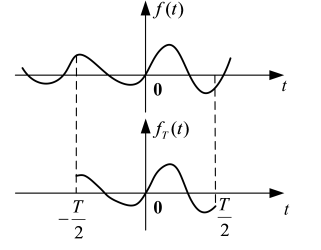
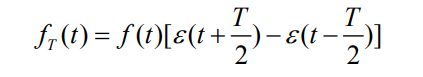
如果T是有限值,则
f
T
(
t
)
f_T(t)
fT(t)的能量也是有限的。令
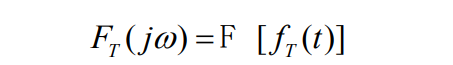
由帕斯瓦尔能量方程,
f
T
(
t
)
f_T(t)
fT(t)的能量
E
T
E_T
ET可表示为:
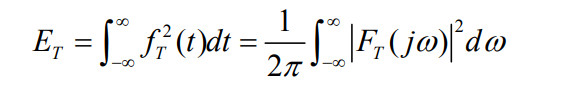

2.2 功率密度谱

2.3 功率密度谱与自相关函数的关系



《工程信号与系统》作者:郭宝龙等
中国大学MOOC:信号与系统 ,西安电子科技大学,郭宝龙,朱娟娟
最后
以上就是大胆火龙果最近收集整理的关于【信号与系统】(十七)傅里叶变换与频域分析——能量谱和功率谱能量谱和功率谱的全部内容,更多相关【信号与系统】(十七)傅里叶变换与频域分析——能量谱和功率谱能量谱和功率谱内容请搜索靠谱客的其他文章。








发表评论 取消回复