目录
- OpenGL
- 图形学
- 数学问题
OpenGL
-
各种矩阵:
- 世界矩阵(World Matrix):世界矩阵确定一个统一的世界坐标,用于组织独立的物体形成一个完整的场景;
- 视图矩阵(View Matrix):摄像机/观察者的位置等信息,将所有世界坐标转换为观察坐标
- 投影矩阵(Projection Matirx):投影矩阵就是3维物体的平面影射.把三维场景在一个二维的平面上显示。裁剪坐标,转换到屏幕上。
- 模型矩阵(Model Matrix):主要针对模型的平移、旋转、缩放等功能,将模型由局部空间转换到世界空间。
- 纹理矩阵:对生成的纹理坐标进行坐标变换。使用纹理坐标变换可以对纹理坐标进行诸如平移、旋转和缩放等三维变换。可以通过一个简单的平移矩阵对纹理坐标进行变换,从而使物体表面上的纹理不断变换位置,产生动画效果。纹理坐标自动生成在三维图形程序中最广泛的应用是环境映射。
-
OpenGL常用的坐标空间
- 局部空间(物体空间):指对象所在的坐标空间
- 世界空间:相对于世界的坐标。物体变换到的最终空间就是世界坐标系。
- 观察空间(摄像机空间/视觉空间):经常被人们称之为OpenGL的摄像机,就是将对象的世界空间的坐标转换为用户视野前面的坐标。因此观察空间就是从摄像机角度观察到的空间。
- 裁剪空间(视觉空间):在一个顶点着色器运行的最后,OpenGL期望所有的坐标都能落在一个给定的范围内,且任何在这个范围之外的点都应该被裁剪掉。被裁剪掉的坐标就被忽略了,所以剩下的坐标就将变为屏幕上可见的片段。
- 屏幕空间:一般由glViewPort设置。
-
OpenGL的渲染流程
-
shader的使用过程
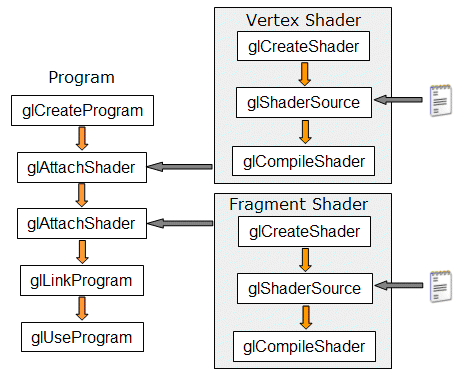
- 顶点着色程序的源代码和片段作色程序的源代码要分别保存到一个字符数组里面;
- 创建着色器对象 - glCreateshader();
- 把源码关联到每个着色器对象 glShaderSource();
- 编译着色器 - glCompileShader();
- 创建(着色)程序对象 - 使用glCreaterProgram();
- 关联着色器到程序对象 - glAttachShader();
- 链接程序 - glLinkProgram();
- 激活着色器程序 - glUseProgram() 将OpenGL渲染管道切换到着色器模式;
- 删除着色器和程序
然后,才可以提交顶点。
-
GLSL如何传递数据
- 老版本(GL2.x)
- Uniform变量:外部程序传递给shader的变量,在shader程序内部,uniform变量就像是C++的const,不能被shader程序修改。uniform是全体顶点都使用的同一个变量。
- attribute变量:只能在vertex shader中声明和使用的变量。一般用attribute变量来表示一些顶点的数据,如:顶点坐标,法线,纹理坐标,顶点颜色等。在application中,一般用函数glBindAttribLocation()来绑定每个attribute变量的位置,然后用函数glVertexAttribPointer()为每个attribute变量赋值。attribute是每一顶点各自的变量。
- varying变量:varying变量是vertex和fragment shader之间做数据传递用的。一般vertex shader修改varying变量的值,然后fragment shader使用该varying变量的值。因此varying变量在vertex和fragment shader二者之间的声明必须是一致的。application不能使用此变量。
- 新版本(GL.3x)
- uniform不变
- 使用in和out来代替attribute和varying
- 老版本(GL2.x)
-
顶点缓冲对象VBO:在显卡存储空间中开辟出的一块内存缓存区,用于存储顶点的各类属性信息,如顶点坐标,顶点法向量,顶点颜色数据等。渲染时直接从VBO取数据,不需要从CPU传输数据,效率高。可以开辟多个VBO,每个VBO在opengl中有其唯一的ID,这个ID对应具体的VBO的显存地址,通过ID对特定的VBO内的数据进行存取操作。
- 创建过程:glGenBuffers(开辟显存空间并分配ID)->glBindBuffer(数据类型绑定)->glBufferData(数据传输到显存缓冲区)->glVertexAttribPointer(通知opengl如何解释这些顶点数据)
- VBO保存了一个模型的顶点属性信息,每次绘制前都要绑定顶点的所有信息,当数据量很大时重复这个动作很麻烦。VAO可以把所有配置存储在一个对象中,绘制模型时绑定这个VAO对象即可。
-
顶点数组对象VAO:保存了所有顶点数据属性的状态集合,存储了顶点数据的格式以及顶点数据所需的VBO对象的引用。VAO本身并没有存储顶点的相关属性数据,这些信息是存储在VBO中的,VAO相当于是对很多个VBO的引用,把一些VBO组合在一起进行对象的统一管理。
创建过程:glGenVertexArrays(开辟)->glBindVertexArray(绑定)->glDrawArrays(绘制)VBO和VAO创建关联过程:
/* 1. Generate Vertex Array Object 2. Bind Vertex Array Object 3. Generate Vertex Buffer Object 4. Bind Vertex Buffer Object */ glGenVertexArrays(1, &vaoID[0]); // Create our Vertex Array Object glBindVertexArray(vaoID[0]); // Bind our Vertex Array Object so we can use it glGenBuffers(1, vboID); // Generate our Vertex Buffer Object glBindBuffer(GL_ARRAY_BUFFER, vboID); // Bind our Vertex Buffer Object glBufferData(GL_ARRAY_BUFFER, 18 * sizeof(GLfloat), vertices, GL_STATIC_DRAW); // Set the size and data of our VBO and set it to STATIC_DRAW glVertexAttribPointer((GLuint)0, 3, GL_FLOAT, GL_FALSE, 0, 0); // Set up our vertex attributes pointer glEnableVertexAttribArray(0); // Disable our Vertex Array Object glBindVertexArray(0); // Disable our Vertex Buffer Object delete [] vertices; // Delete our vertices from memory -
索引缓冲对象EBO:相当于opengl中的顶点数组的概念,是为了解决同一个顶点多次重复调用的问题,可以减少内存浪费,提高执行效率。当需要使用重复顶点时,通过顶点的位置索引来调用顶点,而不是对重复的顶点信息重复记录,重复调用。EBO中存储的内容就是顶点为位置的索引indices,EBO跟VBO类似,也是显存中的一块内存缓冲器,只不过EBO保存的是顶点的索引。
创建过程:glGenBuffers(开辟)->glBindBuffer(绑定类型)->glBufferData(输入数据)->glDrawElements(绘制) -
顶点法线和面法线的作用
- 面法线,垂直于平面,位于中央,经常用于flat着色。
- 点的法线是在使用Phone或Gouraud模型时计算光照使用。如果一个面上的所有法线都一样,他们的光照也就一样,就会产生 flatness 效果;而如果把每个顶点的法向设置不同,则更平滑。
-
CPU与GPU之间的调度
- OpenGL主程序由CPU调度运行,图像处理部分通过GLSL交由GPU执行。
- CPU与GPU之间的数据传递分为三个步骤:
- 首先利用 OpenGL函数生成一个ID;
- 根据需要对该ID号码进行内存类型的绑定;
- 经过以上步骤,GPU中用于接收系统内存中数据的标识符就准备好了。然后对这部分内存进行初始化,初始化的内容来自于系统内存中,这一部分功能利用glBufferData函数完成。
- 数据提交到GPU专用的内存中后,需要根据应用场景对这些数据进行适当的分配。比如,哪些数据当作顶点、当作颜色、用于控制光照。
-
OpenGL中的几种缓冲
- 帧缓冲:下面几种缓冲的集合,通过帧缓冲将场景渲染到一个不同的帧缓冲中,存放显示用的数据。像素数据必须通过一系列测试才能写进帧缓存。video controller负责将帧缓冲输出到显示器上。
- 颜色缓冲:存储所有片段的颜色,即视觉输出的效果。
- 深度缓冲:是在三维图形中处理深度坐标的过程,是可见性问题的一个解决方法。根据缓冲的Z值,确定哪些面片被遮挡。由GLFW自动生成。
- 模板缓冲:与深度缓冲类似,模板缓冲可以为屏幕上的每个像素点保存一个无符号整数值。渲染过程中,通过比较模板值和预设值,决定是否更新相应的像素点的颜色值,即决定是否丢弃片段。
- uniform缓冲:可以将大量的需要传递至多个着色器的矩阵、向量数据等存储在uniform buffer中。这是一个公共的缓存,所以当多个着色器需要传递相同的数据时,可以使用uniform buffer,减少代码量。
- 数据在OpenGL中的处理顺序:顶点着色器->片段着色器->模板测试->深度测试
-
mipmap:
- 多级渐远纹理,目前应用最广泛的纹理映射技术之一。就是实现“实物近大远小,近处清晰远处模糊”的效果。简单来说就是一系列的纹理图像,后一个纹理图像是前一个的二分之一。
- 背后的理念:距观察者的距离超过一定的阈值,OpenGL会使用不同的多级渐远纹理,即最适合物体距离的那个。
-
OpenGL为什么不提供窗口操作(没有读取三维模型、图片的接口)
跨平台的特点造成的。因为它可以不依赖硬件和系统,因此就不会包含执行窗口任务的函数,或者处理用户输入等。这些函数是由我们使用的应用或系统来提供。 -
三维数据如何在二维屏幕上显示
- 通过投影将三维坐标转换为二维坐标:
- 透视投影:为了获得接近真实的三维物体效果而在二维平面上绘制、渲染的方法。类似于现实中人对事物的认识(近大远小,远处模糊近期清晰)。
- 正投影:正射投影矩阵定义了一个类似立方体的平截头箱,它定义了一个裁剪空间,在这空间之外的顶点都会被裁剪掉。
- 主要是通过图形渲染管线管理的,被划分为两个过程:
- 把3D坐标转换为2D坐标
- 把2D坐标转换为实际有颜色的像素
- 通过投影将三维坐标转换为二维坐标:
-
GL_LINES、GL_LINE_STRIP 和 GL_LINE_LOOP的区别
- GL_LINES:可以连接每一对相邻点而得到一组直线。如果最后一个端点处于奇数位置,则该点会被忽略。
- GL_LINE_STRIP:会将传入的点依次连接直到最后一个端点。
- GL_LINE_LOOP:在GL_LINE_STRIP的基础上又进行了首尾相连。
-
GL_TRIANGLES、GL_TRIANGLE_STRIP 和 GL_TRIANGLE_FAN的区别
- GL_TRIANGLES:会将矩阵中每三个点取出绘制一个三角形,最后一组不足三个则自动忽略;
- GL_TRIANGLE_STRIP:绘制时满足以下规则:第n(奇数,从1到k)个三角形将会连接n,n+1,n+2三个顶点,对于第n(偶数)个三角形将会连接n+1,n,n+2三个顶点。所以总共会绘制k-2个三角形。
- GL_TRIANGLE_FAN:绘制时满足以下规则:第n(从1到k)个三角形将会连接1,n+1,n+2三个顶点。总共会绘制k-2个三角形。
-
片段和像素的区别
- 片段是渲染一个像素需要的全部信息,所有片段经过测试与混合后渲染成像素。
- 片段是三维定点光栅化后的数据集合, 还没经过深度测试,而像素是片段经过深度测试、模板测试、alpha 混合之后的结果。
- 片段的个数远远多于像素, 因为有的片段会在测试和混合阶段被丢弃, 无法被渲染成像素。
-
OpenGL的四种测试
- 剪裁测试:只有位于指定矩形内部的像素才能通过测试。
- Alpha测试:只有Alpha值与设定值相比较,满足特定关系条件的像素才能通过测试。
- 模板测试:只有像素模板值与设定值相比较,满足特定关系条件的像素才能通过测试。
- 深度测试:只有像素深度值与新的深度值比较,满足特定关系条件的像素才能通过测试。
-
顶点坐标包括哪些数据(位置,像素颜色,索引)
图形学
- 齐次坐标:
- 3D point表示为 [ x , y , z , 1 ] T [x, y, z, 1]^T [x,y,z,1]T;3D vector表示为 [ x , y , z , 0 ] T [x,y,z,0]^T [x,y,z,0]T
- 优点:
- 区分点和向量
- 平移变换不是线性的,无法用矩阵相乘表示。使用齐次坐标可以实现平移操作。
- 支持投影矩阵。
- 仿射变换 = 线性变换 + 平移变化
- 旋转的表示方式
- 欧拉角:通过不同轴的旋转次序的组合来达到旋转的效果
- 四元数
- 旋转矩阵
- 罗德里格旋转公式:一个向量绕旋转轴旋转给定角度以后得到的新向量的计算公式。
- 光照模型的组成
- 环境光:是由光源发出经环境多次散射而无法确定其入射方向的光,即似乎来自所有方向。其特征是入射方向和出射方向均为任意方向。
- 漫反射:来自特定方向,它垂直于物体时比倾斜时更明亮。一旦它照射到物体上,则在各个方向上均匀地发散出去,效果为无论视点在哪里它都一样亮,其特征是入射方向唯一、出射方向为任意方向。与法线与入射光线的方向有关。
- 高光/镜面反射:来自特定方向并沿另一方向反射出去,一个平行激光束在高质量的镜面上产生100%的镜面反射,其特征是入射方向和出射方向均唯一。与反射方向和视线方向(或者是法线与h)有关。
- 光源:点光、定向光、手电筒(聚光灯)
- 光照计算算法
- Blinn-Phong光照模型
- 光线追踪
- 如何渲染半透明物体?BSDF,内表面散射
- PBR(Physically Based Rendering)
使用基于物理原理和微平面理论建模的着色/光照模型,以及使用从现实中测量的表面参数来准确表示真实世界材质的渲染理念。
一个光照模型属于PBR,需满足以下三个条件:- 基于微平面(Microfacet)的表面模型。微表面理论(Microfacet Theory)认为我们看到的表面上的一点是由很多朝向各异且光学平的微小表面组成。
- 能量守恒。
- 应用基于物理的BRDF。
数学问题
- 两个单位矢量叉乘和点乘的几何意义
叉乘还得到三角形的面积。 - 平面上N个点,每两个点都确定一条直线,求出斜率最大的那条直线所通过的两个点。
将所有点按照x坐标进行排序,求相邻两个点的斜率,找最大值。时间复杂度O(NlogN)。 - 点是否在直线上?
直线的两点为AB,判定点是C,只需要计算三角形ABC的面积,面积为0,代表三点在同一条线上。使用叉乘:a×b=|a||b|sinθ。(a,b是AB和AC向量) - 点是否在线段上?
- 首先判断点是否在直线AB上。点C需要在以AB为对角线的矩形内,这限制在AB线段内。【C的每一维坐标必须在AB之间】
- 直接算各坐标的比例
- 点是否在三角形内部?
- 面积法:三角形三个点ABC和点P。计算ABC面积,ABP面积,ACP面积,BCP面积,如果后三个面积相加等于ABC面积,说明在三角形内部。
- 叉乘法:如果点在三角形内部,则按照逆时针,满足P在三条边的左边,可以根据叉乘方向判断,AB和PA叉乘,如果三个叉乘方向都相同,说明在三角形内部。
- 点到直线的距离
- 几何法:给出三个点,A,B和C,求点C到点A、B定出的直线间距离。首先计算向量CB和向量CA的叉乘,除以AB,得到点到直线距离。
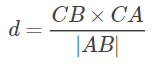
- 解析法:知道AB的直线方程
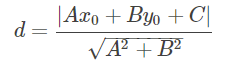
- 几何法:给出三个点,A,B和C,求点C到点A、B定出的直线间距离。首先计算向量CB和向量CA的叉乘,除以AB,得到点到直线距离。
- 直线之间的距离
- 几何法:再一条直线上选取一个点,在另一条直线上选取两个点,转换为计算点到直线的距离。
- 解析法:需要知道直线方程,只有两条直线相互平行(二维空间),才有距离,因此解析方程的AB相同。
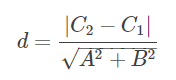
- 三维空间中两条异面直线的最短距离
设两条直线的向量为a和b,将a和b叉乘得到两直线的公共法向量n,在两直线上任意选取A点和B点,得到向量AB,表示为向量c,计算c在公共法向量n上的投影即为两异面直线的最短距离。
d = ∣ n × c ∣ / ∣ n ∣ d = |n × c|/|n| d=∣n×c∣/∣n∣ - 判断两直线是否在一个平面内
在L1上取A,B两点,在L2上取C,D两点,计算AB和AC的叉乘,得到垂直于AB和AC的向量n,若n与CD垂直(点乘为0则垂直),则说明两直线在一个平面内。 - 求空间中两直线的交点O
在直线L2上取一点C,计算出C到L1的距离x,C向L2作垂线交于D,CD长为x。
L1点乘L2得到两直线的夹角θ,由此在三角形OCD中,已知∠COD = θ,∠CDO=90°,CD为x,可计算出OC的距离,由于C坐标已知,OC都位于L2上,可以算出O的坐标。 - 点是否在一个封闭曲线内
点向曲线上一点发射一条射线,判断交点个数 ,若为奇数,则说明点在曲线内部,若为偶数,说明在外部。 - 三维空间中直线是否与三角面片相交?
- 方法一:先计算直线与三角面片所在的平面是否相交,再计算交点是否在三角形内。
- 方法二:直线的解析式是直线上一点+直线向量,将三角面片用重心坐标表示成解析式,计算解析解
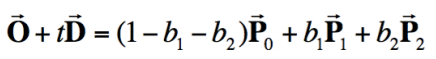
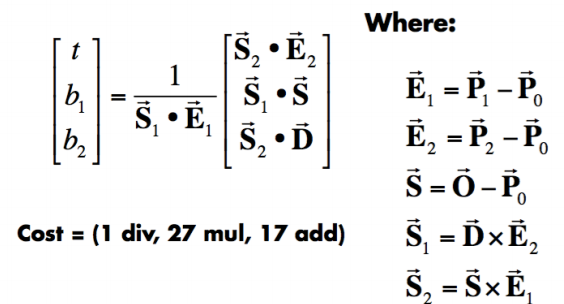
更多一些点线面的关系可看:
《计算机图形学几何工具算法详解》
计算几何算法 http://www.everyinch.net/index.php/computergeometry5/
最后
以上就是狂野外套最近收集整理的关于OpenGL 图形学基础知识汇总OpenGL图形学数学问题的全部内容,更多相关OpenGL内容请搜索靠谱客的其他文章。








发表评论 取消回复