目录
5.5 模型创建
5.5.1 MATLAB中
(1)串/并/反馈
(2)模型互换
5.5.2 Simulink中
(1)直接创建
(2)simulink模型/状态空间模型
5.5 模型创建
5.5.1 MATLAB中
(1)串/并/反馈
| 传递函数的串联*/series |
| ||
| G=G1*G2; | |||
| G=series(G1,G2);%series函数是双目运算 | |||
| [num,den]=series(num1,den1,num2,den2); G=tf(num,den); | |||
| 传递函数的并联+/parallel
|
| ||
| G=G1+G2; | |||
| G= parallel(G1,G2) | |||
| 即:[num,den]=parallel(num1,den1,num2,den2); G=tf(num,den); | |||
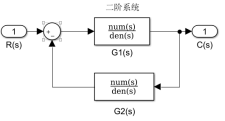
| 闭环联接feedback
|
|
| |
| G= feedback(G1,G2,sign);(最常用) [num,den]=feedback(num1,den1,num2,den2,sign); 将系统G1定义为前向、G2定义为反馈连接成闭环系统; sign=-1或缺省是负反馈,sign=1是正反馈; 特殊的,G= feedback(G1,1,sign);称为单位反馈闭环系统(最常用) | |||
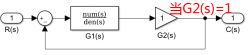
| 单位反馈cloop |
|
| |
| G= cloop (G1,G2, sign); [numc,denc]=cloop(num,den,sign) ; 将系统G1、G2都定义为前向,连接成单位反馈闭环系统; 特殊的,G= feedback(G1,sign);即G2(s)=1时可省略(最常用)
| |||
(2)模型互换

[z,p k]=tf2zp(num,den) 从传递函数模型获取零极点增益
[num,den]=zp2tf(z,p,k) 从零极点模型获取分子分母多项式
5.5.2 Simulink中
(1)直接创建
| 模块名 | 图标 | 功能 |
| Derivative |
| 求输入信号微分(导数) |
| Integrator |
| 求输入信号积分 |
| State Space |
| 线性系统状态空间模型 |
| Transfer Fcn |
| 传递函数模型 |
| Zero pole |
| 零极点模型 |
| PID Controller |
| PID控制 |
| Transport Delay |
| 固定时间传输延迟 |
| Variable Transport Delay |
| 可变时间传输延迟 |
(2)simulink模型/状态空间模型
linmod 从以 Simulink 模型描述的常微分方程组中获取线性模型,通过对模型中的每个模块分别进行线性化,在工作点附近提取连续时间线性状态空间模型。
若simulink模型中含有微分derivative、传输滞后transport delay 模块时,需要先分别利用Simulink Extras-Linearization库下的Switched derivative for linearization、Switched transport delay for linearization模块替换后,才可利用linmod进行线性化转化。
| linmod |
根据指定的状态变量 x 和输入 u 围绕某个工作点(平衡点)获取 sys 的线性化模型,如果您省略 x 和 u,则默认值为零 |
以传递函数形式返回线性化模型。 | |
| |
| delinmod | 获取离散系统模型的线性化模型 |
| ss2tf | [num,den]=ss2tf(A,B,C,D); %将状态空间模型转换为传递函数模型 |
| ‘sys’-需要进行线性化的模型系统的名称,先simulink创建模型保存名为sys; x-状态 (x) ; u-输入(u) 向量; | |
例子:

- 步骤1:建立simulink动态结构图
按照系统结构图,在simulink模块库中,选择相应模块,得到系统的动态模型,并将模型存为“samples1”文件
- 步骤2:求取系统的线性状态空间模型
在MATLAB命令窗口中运行以下命令,得到一个线性状态空间模型(A,B,C,D)
[A,B,C,D]=linmod(‘samples1’); %提取simulink模型的线性状态空间模型
- 步骤3:求系统的传递函数模型
[num,den]=ss2tf(A,B,C,D); %将状态空间模型转换为传递函数模型
printsys(num,den,’s;) %以传递函数形式显示出来
最后
以上就是着急冷风最近收集整理的关于MATLAB/simulink控制系统之各种模型创建/总结(0基础)5.5 模型创建的全部内容,更多相关MATLAB/simulink控制系统之各种模型创建/总结(0基础)5.5内容请搜索靠谱客的其他文章。


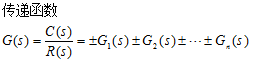
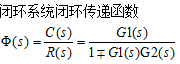














发表评论 取消回复