用Matlab处理信号从入门到入土1

送给哈里森小可爱。

/wwww/

Matlab是分析信号、模拟信号传输过程的重要工具，它的本质就是矩阵运算。对信号的分析过程也就是对表示该信号的矩阵的运算过程。

本文将介绍一些最基础的用matlab进行信号处理的方法，来帮助读者快速入门。

0. matlab安装

csdn上就有很多教程，可以挑一篇自己看得懂的安装。

https://blog.csdn.net/u011344545/article/details/84971945?ops_request_misc=%25257B%252522request%25255Fid%252522%25253A%252522161225219216780274191609%252522%25252C%252522scm%252522%25253A%25252220140713.130102334..%252522%25257D&request_id=161225219216780274191609&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_click~default-1-84971945.pc_search_result_no_baidu_js&utm_term=matlab%25E5%25AE%2589%25E8%25A3%2585

1. 怎么开始写matlab文件

我用matlab一般会写两种文件：脚本文件与函数。

函数：顾名思义，由输入输出与执行部分组成，可以没有输出，但一般有输入。函数的内容可以放在脚本里，但为了更加清晰便于调用或修改，一般单独拆除。

脚本文件：在命令行输入的语句的总和，不存在输入输出。如果要求比较简单，也可以直接在脚本中进行数据处理。

使用[主页]->[新建]->[脚本]/[函数] 新建新的文件

下文将以简单的脚本文件为例，构造并分析一个简单的低频信号。

2. 写matlab脚本最好培养的好习惯，及时清掉历史数据

常见的有一下五个：

clc：清除命令窗口的内容，对工作环境中的全部变量无任何影响 

close：关闭当前的Figure窗口 

close all:关闭所有的Figure窗口 

clear：清除工作空间的所有变量 

clear all：清除工作空间的所有变量，函数，和MEX文件

其中，figure窗口即为输出图像窗口，后文给出如何绘制对应图像；工作空间即为工作区，默认位于matlab右侧边栏处，也可以通过调整布局将它放在自己喜欢的位置。

因此，我写的脚本文件的开头为：

%% 清除历史信息
clc;
clear all;
close all;

%为Matlab中的注释符号，不参与运算； %% 可以将文章分割得更加清晰

另外，matlab中注释的快捷键为ctr+R；去掉注释的快捷键为ctr+T。

3. 构建一个简单的低频信号

matlab中数组的不需要定义，假设我们需要分析一个sinc函数（https://baike.baidu.com/item/sinc函数/5952485?fr=aladdin）

直接在自己构建的脚本文件中写入如下部分即可：

y1=sinc(t*200);

sinc为matlab中自带的函数，200为任意指定系数。

常用的函数还有sin, cos（更多参见：https://ww2.mathworks.cn/help/matlab/elementary-math.html?s_tid=CRUX_lftnav ）

但此时，t没有赋值，是不可以直接使用的，因此我们还需要在sinc函数前定义一下t的范围。

代码如下：

t=-2:0.0001:2;

这一语句表示t是范围由-2到2，间隔为0.001的一围数组，想要看t的具体数值可以在命令行中输入上述语句，然后在工具区查看。这也是在使用matlab解决实际问题时常用的一个方法，当不确定哪里有问题的时候，点开工作区的数组看看就明白了。

4.画出该低频信号

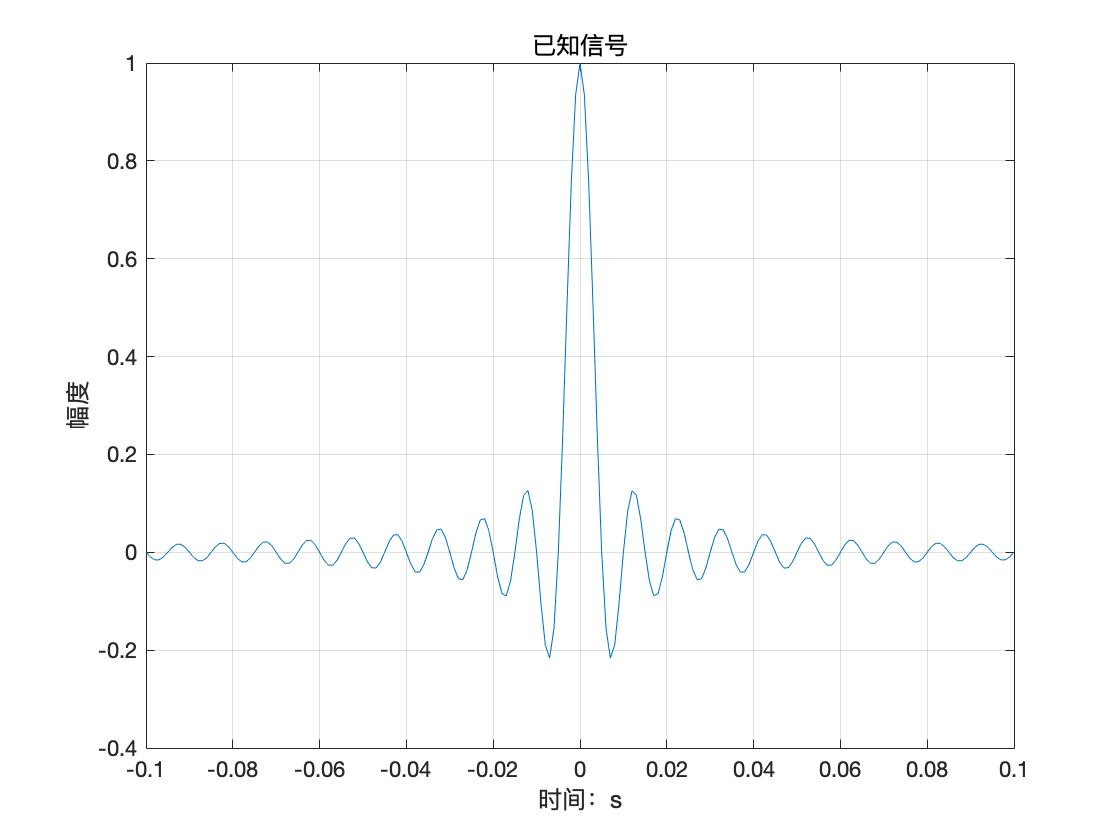
根据上述两句构建的信号为时域信号，我们可以画出对应的信号时域图像。用到的语句如下：

figure;
plot(t,y1)
title('已知信号')
xlabel('时间：s')
ylabel('幅度')
grid
xlim([-0.1,0.1])

其中，

figure：新建一个图像；

plot：画线图，在处理一维信号，如声音信号中常用，示例为最常见用法，更多用法见链接： https://ww2.mathworks.cn/help/matlab/ref/plot.html

title：图像标题

xlabel: 横坐标

ylabel: 纵坐标

grid：画出网格

xlim：x轴范围

结果如下：

5. 对信号进行频域分析

matlab设有专门的进行傅里叶变换的函数fft，由于matlab为矩阵运算，也就是说，傅里叶变换的过程也是在计算离散傅立叶变换（https://baike.baidu.com/item/离散傅里叶变换/6379901?fr=aladdin）。

离散傅里叶变换区别于连续傅里叶变换比较重要的性质有：

在长度为N的离散信号中，针对k=(0,1,2...)，分别找出在长度N内振动k个周期的三角波分量的权值；

也就是说，在Matlab中的DFT依旧是在做有限长度矩阵的运算。

而fft和dft的区别主要在于应用了蝶形运算，处理起来更快一些，本质上就是在做dft运算。更多说明与用例可以参考：https://ww2.mathworks.cn/help/matlab/ref/fft.html?searchHighlight=fft&s_tid=srchtitle

代码如下：

y2 = fft(y1,50000);                 %对信号做傅立叶变换

此时即可得到未经处理的信号频域形式；

此外，可以使用fftshift信号把零频域信号搬至频谱中央，这样做的目的是便于构造低通滤波器，在本科的图像信号处理课程中常有用到。

为了输出频域信号的功率谱，根据功率的定义还应该求解信号的绝对值，并将结果用角度制表示。

abs：matlab中求解绝对值的函数

pi：matlab中圆周率常数的表示方法

因此求解频域信号幅频响应的代码为：

fs = 3000;
y2 = fft(y1,50000);
y3 = 2*pi/40000*abs(fftshift(y2));
f3 = [-25000:24999]/50000*fs;

figure;
plot(f3,y3);
title('已知信号的频谱')
xlabel('频率：hz')
ylabel('幅度')
grid
xlim([-30,30])

需要注意的是，fs为抽样频率，单位为赫兹，表示每秒采样数，采样点为50000，因此横坐标单位为赫兹。在我本科学习信号处理的过程中，经常因为搞不清横坐标而头疼，其实觉得迷糊的时候画一下就很清楚了。

输出结果为：

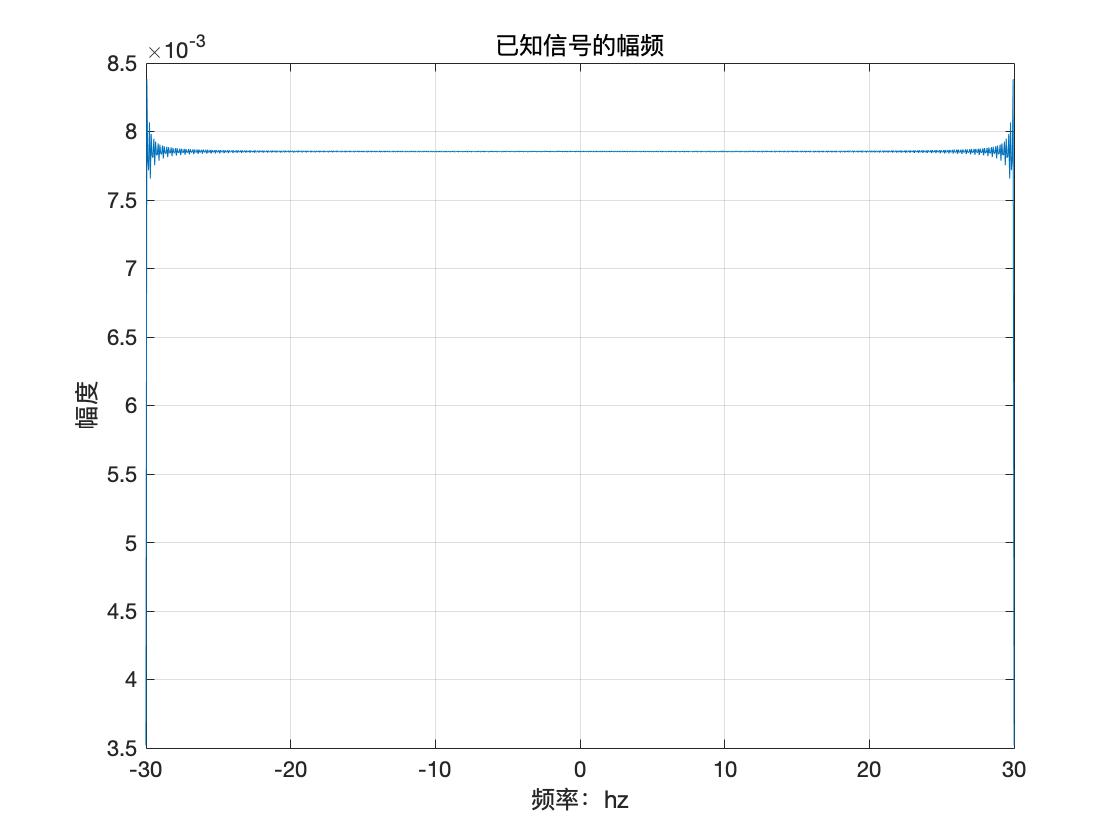
在这部分输出图像中可以看出，sinc函数的幅频响应为近似的矩形窗口，与sinc和矩形窗的傅里叶变换相符合，又因为matlab只能进行有限维的运算，相当于sinc函数是离散且有边界的，所以矩形窗口的形状并不是纯粹的直线，数据越丰富，输出结果就与理论值越相近。

接下来，分析相频信号：

y4 = angle(y3);
figure;
plot(f3,y4);
title('已知信号的相频')
xlabel('频率：hz')
ylabel('幅度')
grid
xlim([-30,30])

其中，angle为求相频的公式，可以直接调用。

结果为：

此时的相频响应其实作用并不大，但在PM调制或QAM调制中，相频响应对理解调制的效果很有帮助。

以上内容为对某一确定信号的最基础的幅频相频分析，可以尝试构造一个由不同频率三角函数构成的信号，并应用fft，abs与angle尝试处理输出该信号，可以更好地理解幅频相频响应，下一期将介绍简单的调制解调过程。

这个内容是为了帮助大家入门matlab处理信号的胎教级别教程，因为是心血来潮写的，所以考虑或许会不周全，结构也不严谨，也可能会有说得不准确的地方，如果有什么问题，欢迎大家留言指出，不胜感激！

最后

以上就是忧心蜜蜂为你收集整理的用Matlab处理信号从入门到入土1的全部内容，希望文章能够帮你解决用Matlab处理信号从入门到入土1所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。