序列周期延拓

编写周期延拓函数

function[ny,y]=SeqZQYT(nx,x,L,k)
%将x(n)以L为周期延拓，自x(n)起始点给出k个周期
N=length(nx);
ny=min(nx):k*L+min(nx)-1;
y=zeros(1,k*L);
for i=0:k*L-1;
    if L==N
        y(i+1)=x(mod(i,L)+1);
    end
    if L>N
        x1=[x zeros(1,L-N)];
        y(i+1)=x1mod((i,L)+1)
    end
    if (L<N)&(L>N/2)
        x2=[x(1:N-L)+x(L+1:N)x(N-L+1:L)];
        y(i+1)=x2(mod(i,L)+1);
    end
    if L<N/2
        if mod(N,2)==1
            xb=[x zeros(1,fix(N/2)-1)];
        else
            xb=[x zeros(1,N/2)];
        end
        x3=xb(1:L);
        if mod(N,L)==0
            for t=1:fix(N/L)
                x3=x3+xb(1+t*L:(t+1)*L);
            end
        end
        y(i+1)=x3(mod(i,L)+1);
    end
end

%周期延拓 调用已编写函数
close all;
nx=-4:4;
x=[1 2 3 4 5 6 7 8 9];
L1=3;L2=4;L3=7;L4=9;L5=12;k=3;
[ny1,y1]=SeqZQYT(nx,x,L1,k);
[ny2,y2]=SeqZQYT(nx,x,L2,k);
[ny3,y3]=SeqZQYT(nx,x,L3,k);
[ny4,y4]=SeqZQYT(nx,x,L4,k);
[ny5,y5]=SeqZQYT(nx,x,L5,k);
subplot(3,2,1)
stem(nx,x,'.');grid on;axis([-5 5 -1 10]);
xlabel('nx');ylabel('x(n)');title('原序列');
subplot(3,2,2)
stem(ny1,y1,'.');grid on;axis([-5 8 -1 25]);
xlabel('ny1');ylabel('y1(n)');title('T=3');
subplot(3,2,3)
stem(ny2,y2,'.');grid on;axis([-5 10 -1 20]);
xlabel('ny2');ylabel('y2(n)');title('T=4');
subplot(3,2,4)
stem(ny3,y3,'.');grid on;axis([-5 18 -1 15]);
xlabel('ny3');ylabel('y3(n)');title('T=7');
subplot(3,2,5)
stem(ny4,y4,'.');grid on;axis([-5 25 -1 12]);
xlabel('ny4');ylabel('y4(n)');title('T=9');
subplot(3,2,6)
stem(ny5,y5,'.');grid on;axis([-5 32 -1 12]);
xlabel('ny5');ylabel('y5(n)');title('T=12');

序列对称分解

函数

function [ny,y,n,xe,xo] = SeqDCFJ(nx,x,M)
%y-翻转移位后的序列
%  ne-偶对称 no-奇对称
ny=-fliplr(nx)+M;y=fliplr(x);
n=min(min(nx),min(ny)):max(max(nx),max(ny));
xx=zeros(1,length(n));yy=xx;
xx((n>=min(nx))&(n<=max(nx)))=x;
yy((n>=min(ny))&(n<=max(ny)))=y;
xe=(xx+yy)/2;xo=(xx-yy)/2;
end

调用

%序列对称分解
clear;
nx=-2:5;x=[1 2 3 4 5 5 5 5];M=2;
[ny,y,n,xe,xo]=SeqDCFJ(nx,x,M);
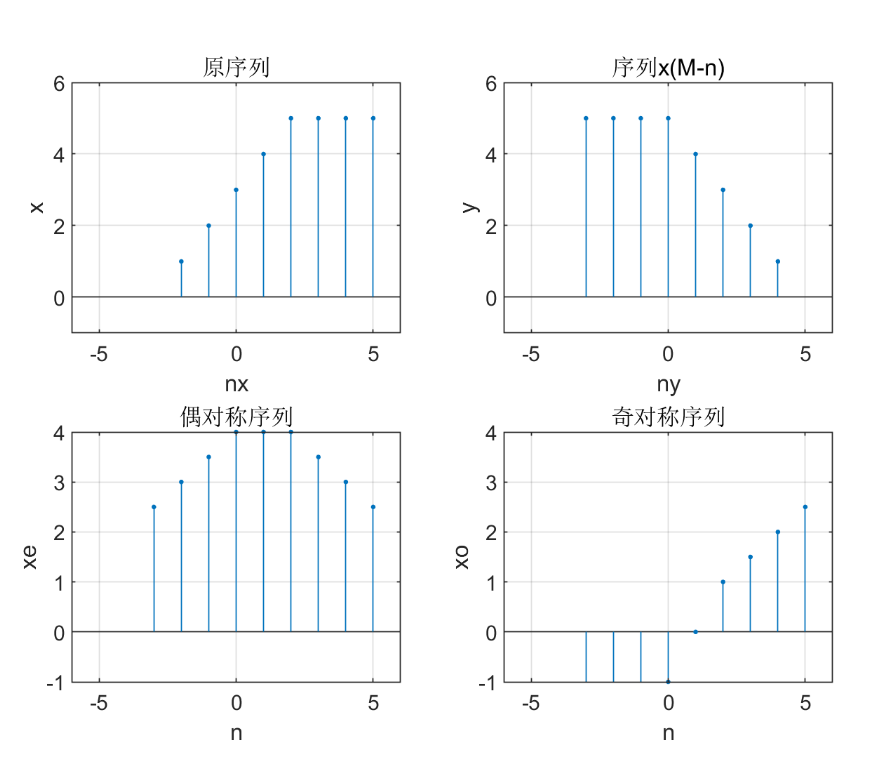
subplot(2,2,1)
stem(nx,x,'.');axis([-6 6 -1 6]);grid on;
xlabel('nx');ylabel('x');title('原序列')
subplot(2,2,2)
stem(ny,y,'.');axis([-6 6 -1 6]);grid on;
xlabel('ny');ylabel('y');title('序列x(M-n)')
subplot(2,2,3)
stem(n,xe,'.');axis([-6 6 -1 4]);grid on;
xlabel('n');ylabel('xe');title('偶对称序列')
subplot(2,2,4)
stem(n,xo,'.');axis([-6 6 -1 4]);grid on;
xlabel('n');ylabel('xo');title('奇对称序列')

最后

以上就是舒服钻石为你收集整理的3.离散序列的表示与基本运算（二）序列周期延拓序列对称分解的全部内容，希望文章能够帮你解决3.离散序列的表示与基本运算（二）序列周期延拓序列对称分解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。