本章内容

主要介绍了离散/连续的基本信号，基本运算，基本分解。

基本信号：如正弦信号，实指数序列

基本运算：如反转，微分/差分。积分/求和

基本分解：直流/交流分量，奇偶分量，实部/虚部分量。

信号可以表示为δ信号是时域分析的要点。

连续时间信号是 δ信号的线性组合；离散时间信号是delte[K]的线性组合

连续时间基本信号

普通信号：直流，正弦，指数类，抽样 信号

奇异信号：阶跃，冲激，胁迫，冲激偶 信号

直流：

y=c

正弦

A w 相位

实指数

x(t)=Ae^at

比如 电容充放电

虚指数

x(t)=e^jwt=coswt+jsinwt

虚指数和正余弦信号可以互相线性表示，统称为正弦类信号

复指数信号

x(t)=Ae^st, s=o+jw

它的实部和虚部都是一个幅值按指数变化的正弦函数。

弹簧带阻尼的振动就是复指数信号

抽样

Sa(t)=sin(t)/t

性质：

Sa(0)=1

Sa(kpi)=0

从负无穷到正无穷的积分= pi

奇异信号

函数本身或其导数或高阶导数具有不连续点（跳变点）。（不光滑）

1. 阶跃响应

u(t)
比如开关电路

2. 单位冲激

狄拉克
特点：
积分为1
f(x)和单位冲击函数相乘再积分，结果是f(0)

特性：

利用这些特性可以求解一些积分问题
推论：
偶函数

3. 单位斜坡

r(t)

4. 单位冲激偶信号

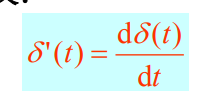
关系：

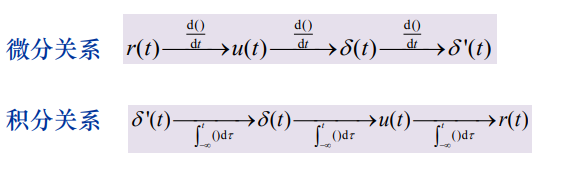
信号处理

1. 反转

关于y轴反转
x(t)->x(-t)

2. 尺度变换

包括压缩和展开
x(t)->x(at)
如音量的快进，慢速播放

3. 时移

x(t)->x(t±t0)
向左向右移动

上述3种，端点函数值不变，端点还是端点

4. 相加

对应点相加
x(t) = x1(t)+x2(t)

5. 相乘

对应点函数值相乘
如信号的调制
如把440Hz正弦波，乘以4Hz正弦波，就得到振音（把4Hz看成整幅，就是一个幅值是正弦波的正弦波）

6. 微分

求导

7. 积分

如果原函数不含冲激函数，积分连续

离散时间基本信号

指数序列，单位脉冲序列，单位阶跃序列，矩形序列，斜坡序列

1. 实指数序列

X[k]=Ar^k
如人口的增长，电池电量
r<0时，是一个正负变化

2. 虚指数序列&正弦序列

虚指数序列&正弦序列 统称为正弦类信号
x[k] = e^jΩ0k x[k] = Acos(Ω0k+o/）
如果Ω0满足 e^jΩ0N=1，即Ω0N = m2Π，那么信号时周期信号，周期为N。
判断方法，看2Π/Ω是不是有理数

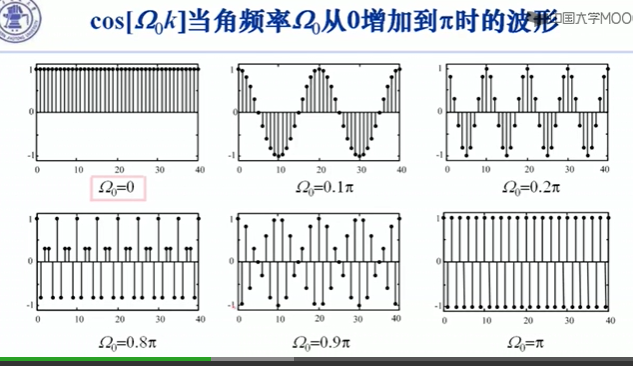
一个周期里面有这么多个点：2Π/Ω

3. 复指数序列

它的实部和虚部都是一个幅值按指数变化的正弦函数。

4. 单位脉冲序列

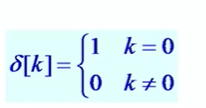
可以用来表示任意离散时间序列

5. 单位阶跃序列

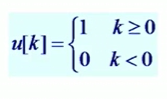
单位脉冲式单位阶跃的差分，单位阶跃是单位脉冲的求和

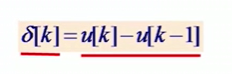
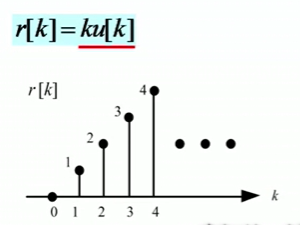
6. 单位斜坡序列

离散时间信号的基本运算

翻转，位移,

1. 翻转，

x[k]->x[-k]

2.位移

x[k]->x[k±n]

3. 抽取和内插

抽取：如音频文件压缩，会损失信息
x[k]->x[Mk]

内插：差的是零，不是中间值

4. 序列相加

对应点相加

5. 序列相乘

对应点相乘

6. 差分

7. 求和

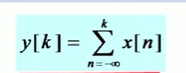
信号时域分解

基本分解：直流/交流分量，奇偶分量，实部/虚部分量。δ信号的组合

直流/交流分量

直流分量怎么求
连续：xDC = 1/(a-b)*a到b上的积分
离散：xDC[k] = 1/(N2-N1+1) * Σx[k]

奇偶分量

连续时间信号的奇信号怎么求
xo(t) = 1/2 * [x(t)-x(-t)]
偶信号怎么求
xc(t) = 1/2 * [x(t)+x(-t)]
离散的：
奇：xo[k] =1/2(x[k]-x[-k])
偶：xc[k] =1/2(x[k]+x[-k])

实部/虚部分量

对于一个复信号，可以这样分解
怎么求：利用共轭信号，相加除以2就是实部

表达为δ信号

连续：x(t) = ∫x(T)δ(t-T)dT
或者：x(t) = Δ趋于零，k从-∞到+∞, Σx(kΔ)δ(t-kΔ)Δ

意义：不同连续信号都可以表示为冲激信号及其时移的线性组合。不同信号只是他们的系数不同。
应用：求解输入信号通过线性时不变系统时的响应时，只需要求解冲激函数的响应，然后利用系统的特性（叠加原理），就可以求出零状态响应

离散：x[k] = n从-∞到+∞，Σx[n]δ[k-n]

最后

以上就是苹果盼望为你收集整理的信号与系统笔记连续时间基本信号离散时间基本信号离散时间信号的基本运算信号时域分解的全部内容，希望文章能够帮你解决信号与系统笔记连续时间基本信号离散时间基本信号离散时间信号的基本运算信号时域分解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。