一、Introduction

1. Signals and Systems信号与系统

(1) Signal信号

A signal is formally defined as a function of one or more variables that conveys information on the
nature of a physical phenomenon.

(2) System系统

A system is formally defined as an entity that manipulates one or more signals to accomplish a function, thereby yielding new signals.

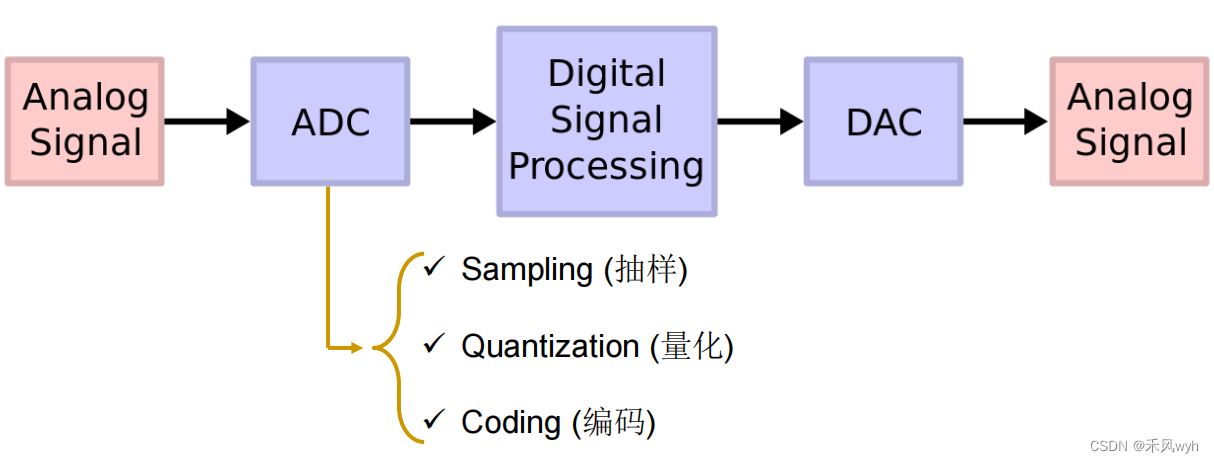
2. Classification of Signals信号的分类

(1) Continuous-time & discrete-time

1) Continuous-Time signal连续时间信号

A continuous-time signal is defined for all time t, except at some discontinuous point.

2) Discrete-Time signal离散时间信号

A continuous-time signal is defined only at discrete instants of time.

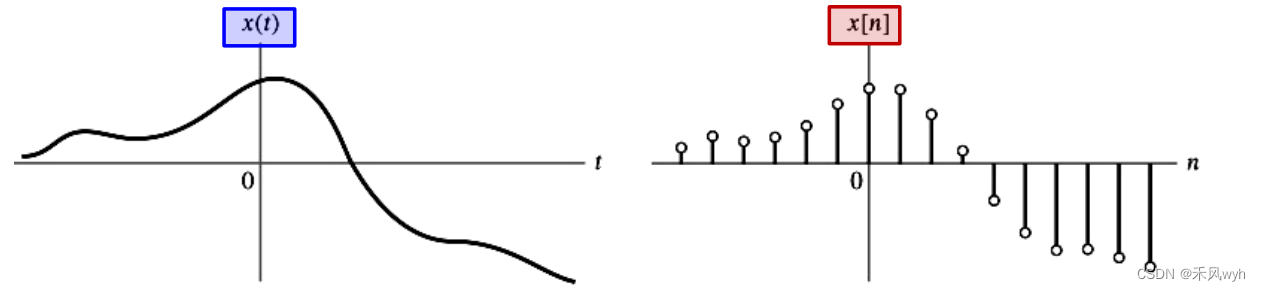
3) Relationship关系

· A discrete-time signal is often derived from a continuous-time signal by sampling (抽样) it at a uniform rate (nT)

x[n]= $x(t){|}_{t=nT}$=x(nT)
T: sampling period, n: an integer
Continuous-time signals: x(t)
Discrete-time signals: x[n]=x(n$T_s$), n=0, $\pm$ 1, $\pm$ 2, $\dots$

(2) Even and odd signals偶奇信号

1) Even signals (偶信号)

Symmetric about vertical axis: x (-t) = x (t), x [-n] = x [n] for all t

2) Odd signals (奇信号)

Antisymmetric about origin: x (-t) = - x (t), x [-n] = x [n] for all t

3) Even-odd decomposition of x(t)奇偶分量

x (t)=$x_e$(t)+$x_o$(t) where $x_e$(-t) = $x_e$(t), $x_o$(-t) = -$x_o$(t)
$\to$ $x_e$(t)=$\frac{1}{2}$[x(t)+x(-t)]
$\to$ $x_o$(t)=$\frac{1}{2}$[x(t)-x(-t)]

4) PRODUCT Rule

ODD $\times$ ODD $\to$ EVEN
EVEN $\times$ EVEN $\to$ EVEN
EVEN $\times$ ODD $\to$ ODD
ODD $\times$ EVEN $\to$ ODD

${\int }_{-T}^{T}x(t)dt$=0 always of x(t) is ODD
=0 sometimes if x(t) is EVEN
${\int }_{-T}^{T}x(t)dt$=2${\int }_0^{T}x(t)dt$ for x(t) EVEN

3. Operation on Signals信号运算

(1) In Time Domain时域

1) Time Scaling时间展缩

y(t) = x (at) $\to$ a>1, compressed; 0<a<1, expanded
y[n] =x [kn] , k>0, k is an integer$\to$some values lost

2) Time Reflection时间反转

y(t)=x(-t)$\to$The signal y(t) represents a reflected version of x(t) about t=0

3) Time Shifting时移

y(t)=x(t-$t_0$) $\to$ $t_0$>0, 右移(shift towards right) ；$t_0$<0, 左移(shift towards left)
y[n]=x[n-m] $\to$ m>0, 右移(shift towards right) ；m<0, 左移(shift towards left)

(2) In Amplitude幅度

1) Amplitude scaling幅度缩放

x(t) $\to$ y(t)=cx(t)
x[n] $\to$ y[n]=cx[n]

2) Addition加

y(t) = $x_1$(t) + $x_2$(t)
y[n] = $x_1$[n] + $x_2$[n]

3) Multiplication乘

y(t) = $x_1$(t) $x_2$(t)
y[n] = $x_1$[n] $x_2$[n]

4) Differentiation 微分

y(t) = $\frac{d}{dt}$x(t)

5) Integration 积分

y(t) =${\int }_{-\infty }^{t}x(\tau )d\tau$

(3) Precedence Rule步骤

1）f(t)$\to$f($\alpha$t+$\beta$)

f(t)$\to$f(t+$\beta$)$\to$f($\alpha$t+$\beta$) $\to$ f(-$\alpha$t+$\beta$)
平移 $\to$ 展缩 $\to$ 反转

2）f($\alpha$t+$\beta$)$\to$f(t)

f(- $\alpha$t +$\beta$) $\to$ f($\alpha$t+$\beta$) $\to$ f(t+$\beta$) $\to$ f(t)
反转 $\to$ 展缩 $\to$ 平移

二、Basic Time Signals基本时间信号

1. Exponential Signals指数信号

(1) Continuous-time

x(t) = Be^αt, B and a are real parameters
a. Decaying exponential, for which α < 0
b. Growing exponential, for which α > 0

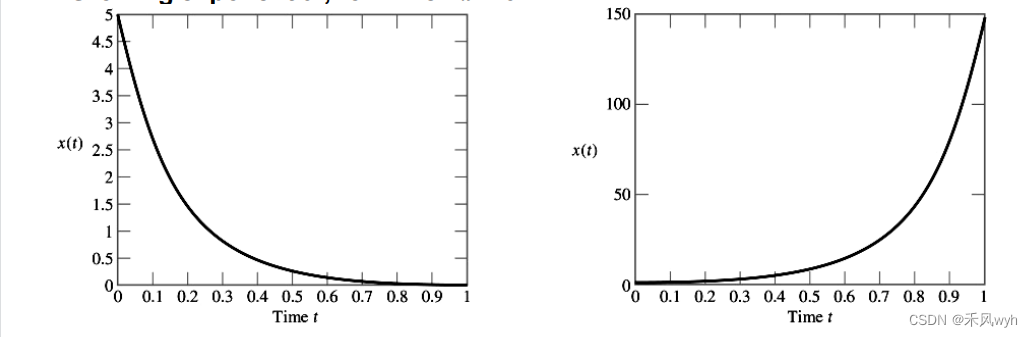
(2) Discrete-time

x[n]=Brⁿ , r=e ^α
a. Decaying exponential, for which α < 0
b. Growing exponential, for which α > 0

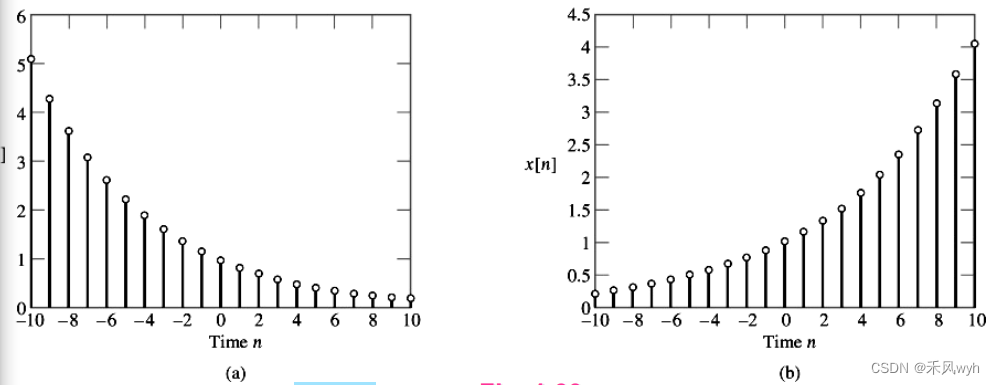
2. Sinusoidal Signals正弦信号

(1) Continuous-time

x (t)=A cos (ωt+φ), T=$\frac{2\Pi }{\omega }$
x (t +T) = x(t)

(2) Discrete-time

x [n] =A cos (Ωn+φ)
Periodic condition: x [n + N] =A cos (Ωn+ΩN+φ)
$\to$ ΩN=2Πm or Ω=$\frac{2\Pi m}{\omega }$

(3) Relation Between Sinusoidal and Complex Exponential Signals

1) Complex exponential signal

Euler’s identity：e^jθ=cosθ+jsinθ
Complex exponential signal: Be^jωt= A e^jφe^jωt=A cos (ωt+φ)+j Asin (ωt+φ)
A cos (ωt+φ)= Re {Be^jωt}
A sin (ωt+φ) = Im {Be^jωt}

2) Discrete-time case

A cos (Ωn+φ) = Re {Be^jΩn}
A sin (Ωn+φ) = Im {Be^jΩn}

3) Two-dimensional representation of the complex exponential e^jΩn for Ω = Π/4 and n = 0, 1…

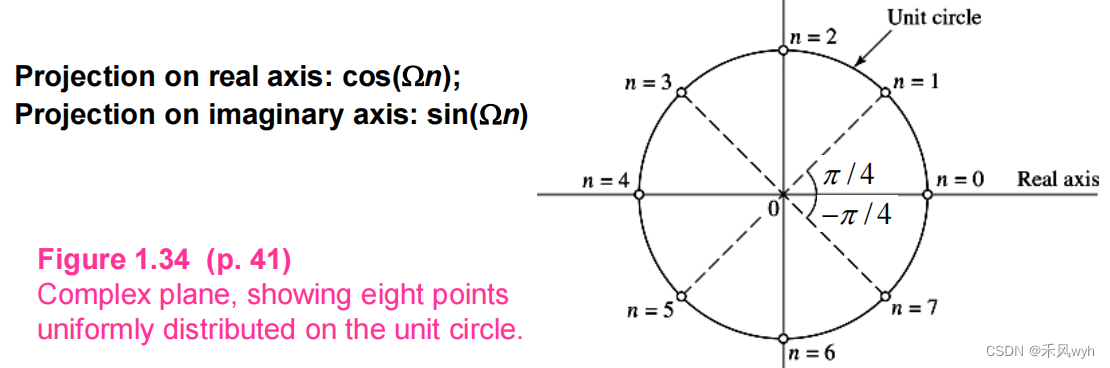
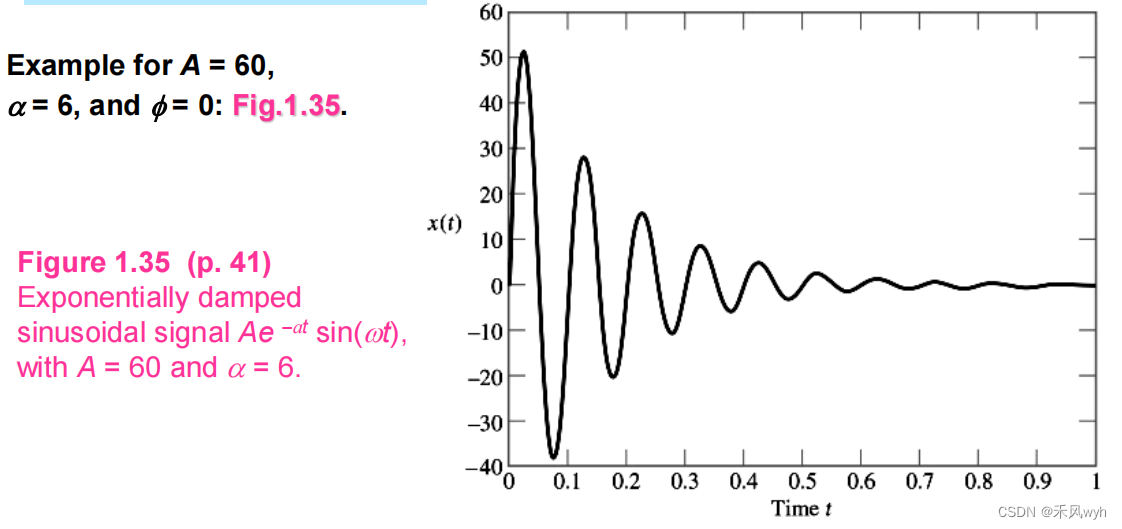
(4) Exponential Damped (衰减) Sinusoidal Signals

x(t)= A e^-αt sin (ωt+φ), α>0

3. Step Functions阶跃信号

(1) Continuous-time

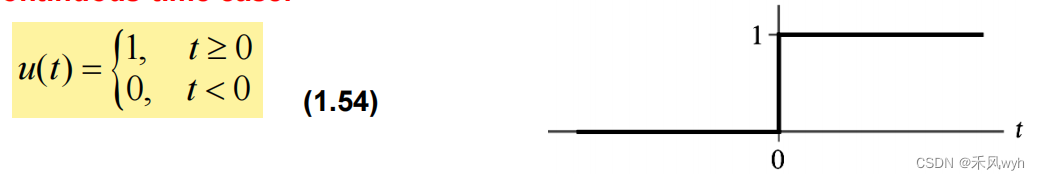
(2) Discrete-time

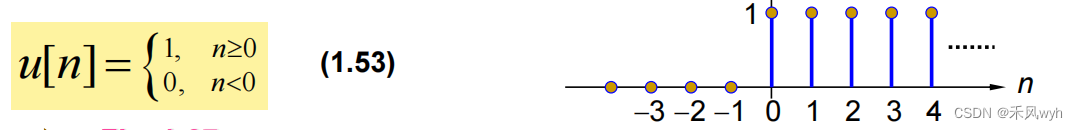
(3) Properties

1) 相乘特性（单边特性）

x(t)u(t)= { x(t) ,t>0
  		    0,t<0

2) 表示作用区间

a. f(t)[u(t-$t_1$)-u(t-$t_2$)]

Rectangular pulse脉冲信号:p(t)=u(t+$\frac{1}{2}$)-u(t-$\frac{1}{2}$)

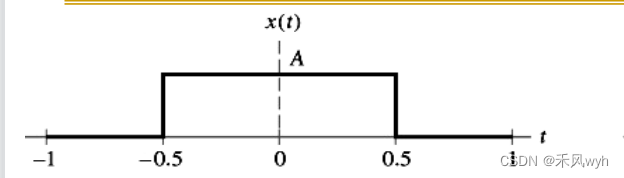
b. 加减

sgn(t) function符号函数
sgn(t)={1,t>0
       -1, t<0
       =u(t)-u(-t)

3) 积分

y(t) =${\int }_{-\infty }^{t}u(\tau )d\tau$=tu（t）=r（t）$\to$ 斜坡信号

4. Impulse Functions冲激信号

(1) Discrete-time

(2) Continuous-time

$\delta$(t)=0 for t ≠0
${\int }_{-\infty }^{\infty }\delta (t)dt$=1

(3) Properties of impulse function

1) Even function偶函数

$\delta$(-t)=$\delta$(t)

2) Sifting property时移特性

$\delta$(t-$t_0$) = 0, t ≠ $t_0$
${\int }_{-\infty }^{\infty }\delta (t-to)dt$=1

3) Time-scaling property展缩特性

$\delta$(at+b)=$\frac{1}{a}$$\delta$(t+$\frac{b}{a}$)

4) Sampling property取样特性

${\int }_{-\infty }^{\infty }x(\tau )\delta (t)dt$=x(0)

x(t)*$\delta$(t-$t_0$)=${\int }_{-\infty }^{\infty }x(t)\delta (t-to)dt$=x($t_0$)

$x(t)\delta (t-to)$=x($t_0$)$\delta$(t-$t_0$)

${\sum }_{i=-\infty }^{\infty }$x(t) $\delta$(k)= x (0)

5) 相乘特性

$x(t)\delta (t)$=$x(0)\delta (t)$
$x(t)\delta (t-to)$=$x(to)\delta (t-to)$

6) Derivatives

7) 与u（t）的关系

δ(t) is the derivative of u(t): δ(t)=$\frac{d}{dt}u(t)$

u(t) is the integral of δ(t): u(t) =${\int }_{-\infty }^t\delta (\tau )d\tau$

u[n] = δ[n]+δ[n-1]+…=${\sum }_{i=0}^{\infty }$ $\delta$[n-k]=${\sum }_{i=-\infty }^n$ $\delta$[m]

δ[n]=u[n]-u[n-1]

三、Systems Classification and Properties系统分类和性质

1. System Representation

2. Continuous-time and Discrete-time Systems

(1) Continuous-time

y(t)=H{x(t)}

(2) Discrete-time

y[n]=H{x[n]}

(3) Moving-average system

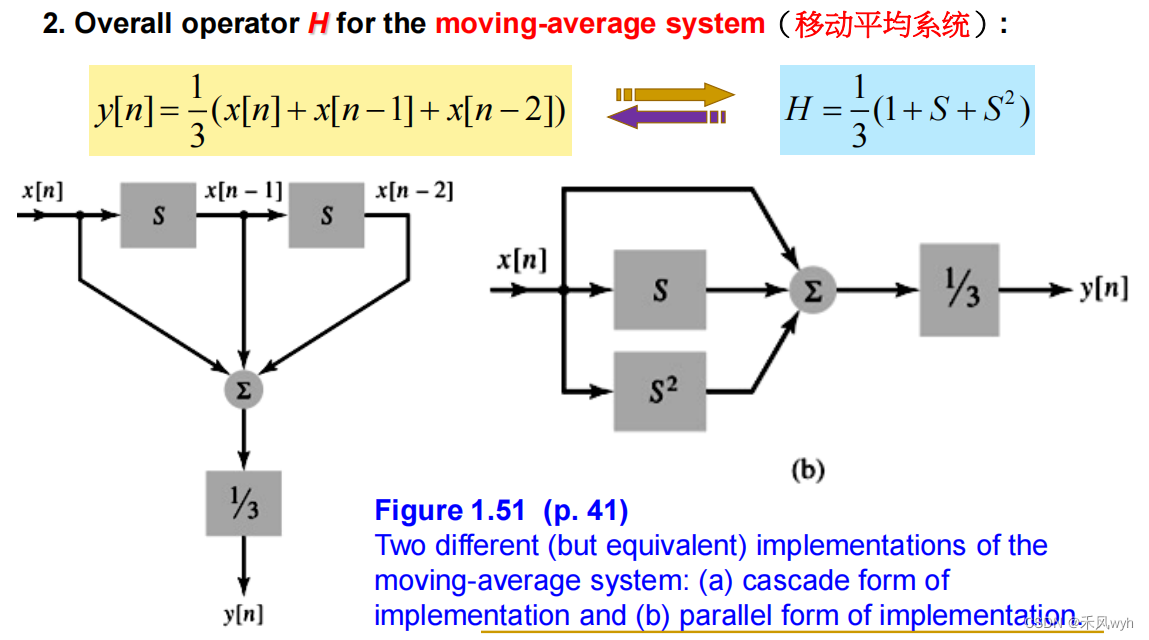
(4) Representation of discrete-time operations

3. Systems with and without memory

(1) without memory

A system is said to be memoryless if the output at any time depends on only the input at that same time.

(2) with memory

A system is said to be memory if the output at any time depends on only the input at past or in the future.

4. Causal and Non-causal systems

(1) Causal

A system is said to be causal if its present value of the output signal depends only on the present or past values of the input signal.

(2) Non-causal

A system is said to be noncausal if its output signal depends on one or more future values of the input signal.

5. Linear and Nonlinear systems

(1) Linear

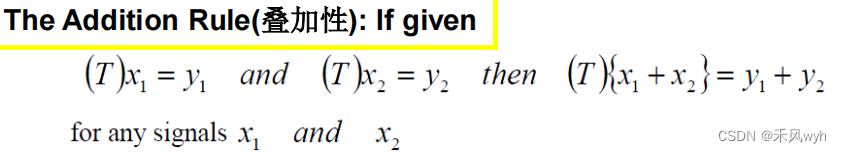
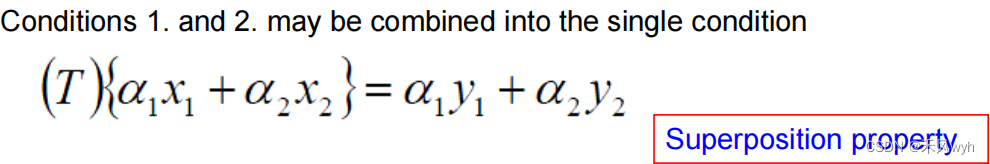
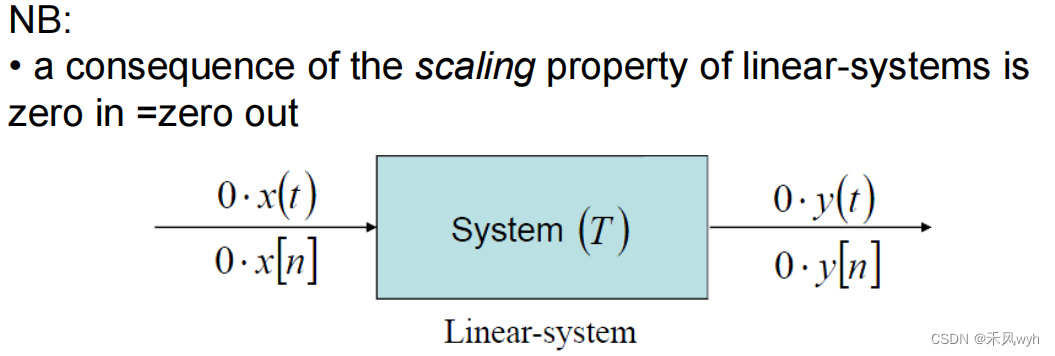
(2) Nonlinear

6. Time-variant and Time-invariant Systems

(1) Time-invariant

(2) Condition for time-invariant system

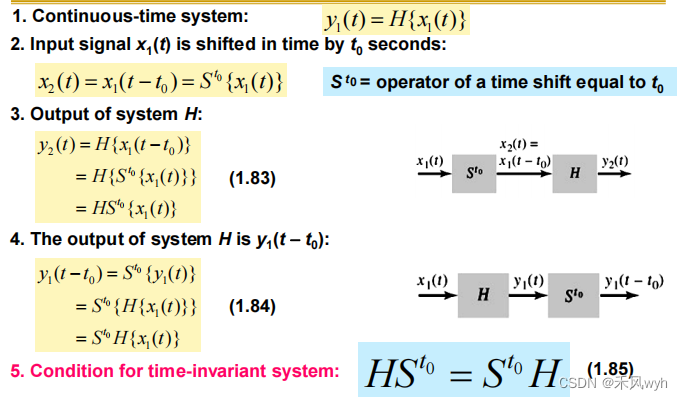
7. Stable systems

A system is bounded-input/bounded-output (BIBO，有界输入有界输出) stable if for any bounded input x defined by |x|≤ $k_1$
The corresponding output y is also bounded defined by |y|≤ $k_2$ where $k_1$ and $k_2$ are finite real constants

8. Feedback systems

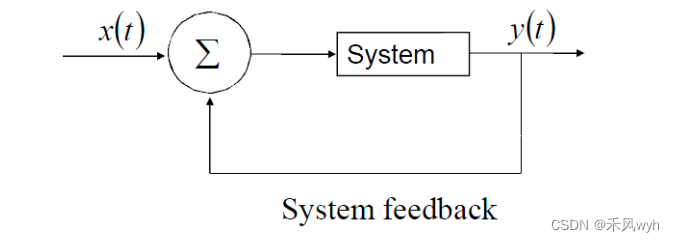
9. Invertibility(可逆性) systems

(1) Continuous-time system

x(t) = input; y(t) = output
H = first system operator; H ${}_{inv}$ = second system operator

(2) Output of the second system

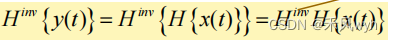
H ${}_{inv}$=inverse operator

(3) Condition for invertible system

H ${}_{inv}$ H= I
I = identity operator （单位算符）

最后

以上就是独特招牌为你收集整理的信号与系统1——Signals and Systems一、Introduction二、Basic Time Signals基本时间信号三、Systems Classification and Properties系统分类和性质的全部内容，希望文章能够帮你解决信号与系统1——Signals and Systems一、Introduction二、Basic Time Signals基本时间信号三、Systems Classification and Properties系统分类和性质所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。