《MATLAB信号处理超级学习手册》——2.3 信号在MATLAB中的运算

本节书摘来自异步社区《MATLAB信号处理超级学习手册》一书中的第2章，第2.3节，作者：MATLAB技术联盟 , 史洁玉著，更多章节内容可以访问云栖社区“异步社区”公众号查看

2.3 信号在MATLAB中的运算

MATLAB信号处理超级学习手册
本节利用MATLAB进行离散时间序列的基本运算，掌握基本的MATLAB函数的编写和调试方法，同时了解对连续时间信号的时域运算，加深对信号的时域运算的理解。

2.3.1 信号的时移、反折和尺度变换
描离散序列的时域运算包括信号的相加、相乘，信号的时域变换包括信号的移位、反折、尺度变换等。在MATLAB中，离散序列的相加、相乘等运算是两个向量之间的运算，因此参加运算的两个序列向量必须具有相同的维数，否则应进行相应的处理。

离散序列的时移、反折、尺度变换与连续时间信号相似，在此举例来说明MATLAB实现过程。

【例2-17】离散序列的时移、反折、尺度变换的实现。运行程序如下：

clear;
k=-12:12;
k1=2.*k+4;
f=-[stepfun(k,-3)-stepfun(k,-1)]+...
    4.*[stepfun(k,-1)-stepfun(k,0)]+...
    0.5*k.*[stepfun(k,0)-stepfun(k,11)];
f1=-[stepfun(k1,-3)-stepfun(k1,-1)]+...
    4.*[stepfun(k1,-1)-stepfun(k1,0)]+...
    0.5*k1.*[stepfun(k1,0)-stepfun(k1,11)];
subplot 221;
stem(k,f);
axis([-12 12 -1 6]);
grid on;
xlabel('n');
ylabel('h(n)');
text(-8,3,'f[k]')
subplot 222;
stem(k+1,f);
axis([-12 12 -1 6]);
grid on;
xlabel('n');
ylabel('h(n)');
text(-9.5,3,'f[k-1]')
subplot 223;
stem(k,f1);
axis([-12 12 -1 6]);
grid on;
xlabel('n');
ylabel('h(n)');
text(-8,3,'f[2k+4]')
subplot 224;
stem(2-k,f);
axis([-12 12 -1 6]);
grid on;
xlabel('n');
ylabel('h(n)');
text(5.5,3,'f[2-k]')

运行程序结果如图2-17所示。

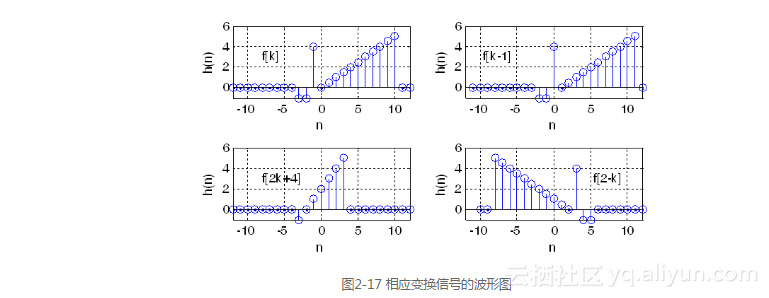
2.3.2 信号的加法和乘法运算
信号的相加和相乘是指同一时刻信号取值的相加与相乘。

对于离散序列来说，序列相加是将信号对应时间序号的值逐项相加，在这里不能象连续时间信号那样用符号运算来实现，而必须用向量表示的方法，即在MATLAB中离散序列的相加需表示成两个向量的相加，因而参加运算的两序列向量必须具有相同的维数。

实现离散序列相加的MATLAB实用子程序如下：

function [f,k]=lsxj(f1,f2,k1,k2)
%实现f(k)=f1(k)+f2(k)，f1，f2，k1，k2是参加运算的二离散序列及其对应的时间序列向量，f和k为返回的和序列及其对应的时间序列向量
k=min(min(k1),min(k2)):max(max(k1),max(k2));
%构造和序列长度
s1=zeros(1,length(k));s2=s1;
%初始化新向量
s1(find((k>=min(k1))&(k<=max(k1))==1))=f1;
%将f1中在和序列范围内但又无定义的点赋值为零
s2(find((k>=min(k2))&(k<=max(k2))==1))=f2;
%将f2中在和序列范围内但又无定义的点赋值为零
f=s1+s2;
 %两长度相等序列求和
stem(k,f,'filled')
axis([(min(min(k1),min(k2))-1),(max(max(k1),max(k2))+1),(min(f)-0.5),(max(f)+0.5)])
%坐标轴显示范围

【例2-18】已知两离散序列分别为：

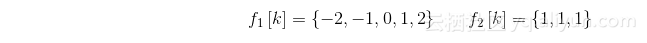
试用MATLAB绘出它们的波形及f 1[k]+ f 2[k]的波形。

运行程序如下：

clear
f1=-2:2;k1=-2:2;
f2=[1 1 1];k2=-1:1;
subplot 221;
stem(k1,f1);
grid on;
xlabel('n');
ylabel('h(n)');
axis([-3 3 -2.5 2.5]);
title('f1[k]');
subplot 222;
stem(k2,f2)
grid on;
xlabel('n');
ylabel('h(n)');
axis([-3 3 -2.5 2.5]);
title('f2[k]');
subplot 223;
[f,k]=lsxj(f1,f2,k1,k2);
grid on;
xlabel('n');
ylabel('h(n)');
title('f[k]=f1[k]+f2(k)');

运行结果如图2-18所示。

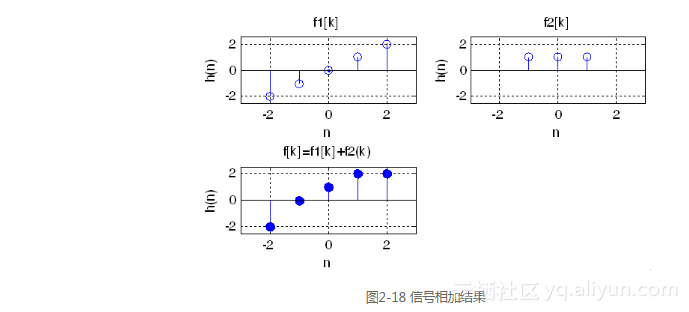
与离散序列加法相似，这里参加运算的两序列向量必须具有相同的维数。实现离散时间信号相乘的MATLAB实用子程序代码如下：

function [f,k]=lsxc(f1,f2,k1,k2)
%实现f(k)=f1(k)+f2(k)，f1，f2，k1，k2是参加运算的二离散序列及其对应的时间序列向量，f和k为返回的和序列及其对应的时间序列向量
k=min(min(k1),min(k2)):max(max(k1),max(k2));
%构造和序列长度
s1=zeros(1,length(k));s2=s1;
%初始化新向量
s1(find((k>=min(k1))&(k<=max(k1))==1))=f1;
%将f1中在和序列范围内但又无定义的点赋值为零
s2(find((k>=min(k2))&(k<=max(k2))==1))=f2;
%将f2中在和序列范围内但又无定义的点赋值为零
f=s1.*s2;
%两长度相等序列求和
stem(k,f,'filled')
axis([(min(min(k1),min(k2))-1),(max(max(k1),max(k2))+1),(min(f)-0.5),(max(f)+0.5)])
%坐标轴显示范围

【例2-19】试用MATLAB绘出上例中两离散序列乘法f 1[k]×f 2[k]的波形。运行程序如下：

f1=-2:2;k1=-2:2;
f2=[1 1 1];k2=-1:1;
subplot 221;
stem(k1,f1);
grid on;
xlabel('n');
ylabel('h(n)');
axis([-3 3 -2.5 2.5]);
title('f1[k]');
subplot 222;
stem(k2,f2);
grid on;
xlabel('n');
ylabel('h(n)');
axis([-3 3 -2.5 2.5]);
title('f2[k]');
subplot 223;
[f,k]=lsxc(f1,f2,k1,k2);
grid on;
xlabel('n');
ylabel('h(n)');
title('f[k]=f1[k]*f2(k)');

运行结果如图2-19所示。

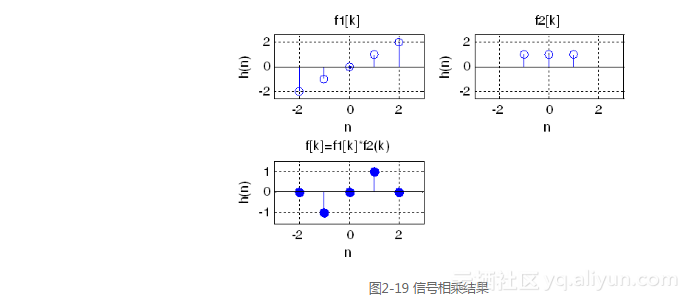
2.3.3 信号的奇偶分解
用户可以利用MATLAB编写的函数sigevenodd()将序列分解成偶序列和奇序列两部分，源程序为：

function****[xe,xo,m]=evenodd(x,n)
if (imag(x)~=0)
        error(‘x is not a real sequence’)；
    end
m=-fliplr(n);m1=min([m,n]);m2=max([m,n]);m=m1:m2;
nm=n(1)-m(1);n1=1:length(n);
x1=zeros(1,length(m));
x1(n1+nm)=x;x=x1;
xe=0.5*(x+fliplr(x)); xo=0.5*(x-fliplr(x));

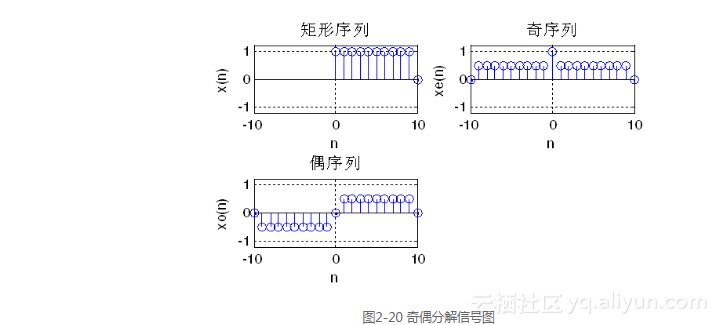
【例2-20】已知x(n)=u(n)-u(n-10)，要求将序列分解为奇偶序列。运行程序如下：

n=[0:10];
x=stepseq(0,0,10)- stepseq(10,0,10);
[xe,xo,m]=evenodd(x,n);
subplot(2,2,1);stem(n,x);
ylabel('x(n)'); xlabel('n');
grid on;
title('矩形序列');axis([-10,10,-1.2,1.2])
subplot(2,2,2);stem(m,xe);
ylabel('xe(n)'); xlabel('n');
grid on;
title('奇序列');axis([-10,10,-1.2,1.2])
subplot(2,2,3);stem(m,xo);
ylabel('xo(n)'); xlabel('n');
grid on;
title('偶序列');axis([-10,10,-1.2,1.2])

运行结果如图2-20所示。

程序运行过程中用到的位阶跃序列的生成函数子程序为：

function [x,n]=stepseq(n0,ns,nf)
n=[ns:nf];x=[(n-n0)>=0];

2.3.4 信号的积分和微分
对于连续时间信号，其微分运算是用diff函数来完成的，其语句格式为：diff(function,'variable',n)

其中，function表示需要进行求导运算的信号，或者被赋值的符号表达式；variable为求导运算的独立变量；n为求导的阶数，默认值为求一阶导数。

连续信号的积分运算用int函数来完成，语句格式为：

int(function,'variable',a,b)

其中，function表示需要进行被积信号，或者被赋值的符号表达式；variable为求导运算的独立变量；a，b为积分上、下限，a和b省略时为求不定积分。

【例2-21】积分运算的实现。运行程序如下：

syms t f2;
f2=t*(heaviside(t)-heaviside(t-1))+heaviside(t-1); 
t=-1:0.01:2;
subplot(121);
ezplot(f2,t);
title('原函数')
grid on;
ylabel('x(t)');
f=diff(f2,'t',1); 
subplot(122)
ezplot(f,t);
title('积分函数 ')
grid on;
ylabel('x(t)')

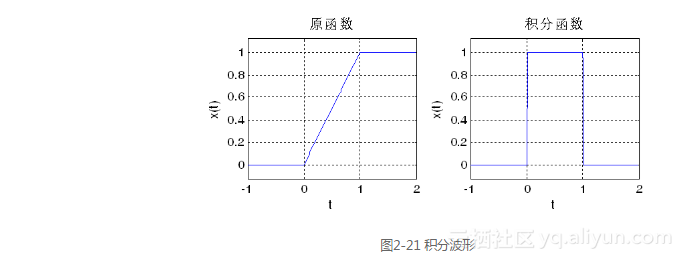
运行结果如图2-21所示。

【例2-22】微分运算的实现。运行程序如下：

syms t f1;
f1=heaviside(t)-heaviside(t-1); 
t=-1:0.01:2; 
subplot(121);
ezplot(f1,t);
title('原函数')
grid on;
f=int(f1,'t'); 
subplot(122);
ezplot(f,t)
grid on
title('微分函数')
ylabel('x(t)');

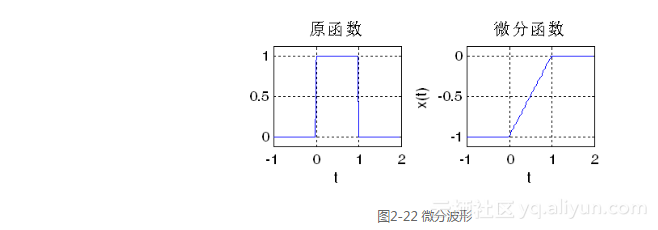
运行结果如图2-22所示。