从频域幅频曲线看系统性能

前边的文章介绍过在时域上系统的特征根对系统特性的影响：
二阶系统欠阻尼状态极点位置对阶跃响应的影响
这里简单回顾下：
典型二阶系统的传递函数如下：
$$H(s)=\frac{\omega n^2}{s^2+2\xi \ast \omega n\ast s+\omega n^2}$$
特征方程为：
$$s^2+2\xi \ast \omega n\ast s+\omega n^2=0$$
欠阻尼状态下的特征根为：
$$s_{1,2}=-\xi \ast \omega n\pm jwn\ast \sqrt{1-{\xi }^2}(0<\xi <1)$$

特征根的实部决定了系统的稳定时间ts，阻尼系数决定了系统的超调量。
$$\begin{gathered} \sigma =e^{\frac{-\pi \ast \xi }{\sqrt{1-{\xi }^2}}} \\ ts=\frac{3.5}{\xi \ast \omega n}（包络线正负百分5） \end{gathered}$$

本文主要包含以下内容：
一、三段法简介
二、低频段对特性的影响
三、中频段对特性的影响
四、高频段对特性的影响

一、三段法简介
三段法即将系统幅频特性区域分为低频段，中频段，高频段三段，其中，低频段主要看系统的开环增益，决定系统的稳态误差；中频段主要看系统的相位余量以及穿越频率，决定系统的稳定时间以及超调量；高频段要求系统看系统的开环增益，决定系统的高频抗干扰能力。

二、低频段
通常指第一个转折频率左侧的频段，这一段的特性由积分环节和开环增益决定，设低频段对应的传递函数为：
$$Gd(s)=\frac{K}{s^v}$$
从《控制系统稳态误差（静态误差）分析》文章介绍
v决定系统的型别，K决定不同型别下不同响应的稳态误差：

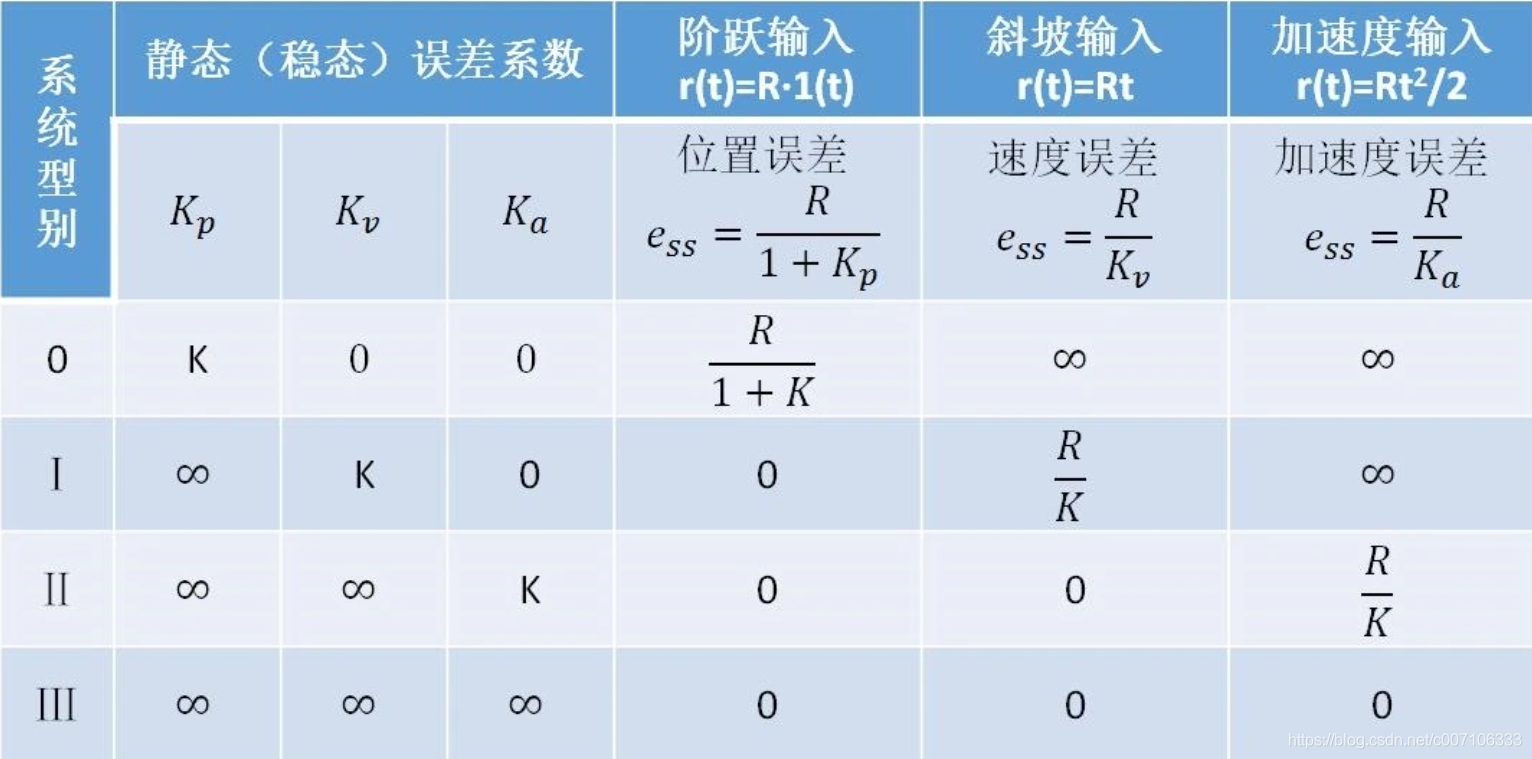
因此在设计系统时，我们需要根据稳态误差要求来确定最小需要的开环增益k.

三、中频段
通常中频段指截止频率附近的频段，相位裕度γ与阻尼系数ξ相关，确定相位余量后，系统的开环截止频率ωc决定了系统的稳定时间ts。
具体而言：
$$\gamma =arctan\frac{2\xi }{\sqrt{\sqrt{4{\xi }^4+1}-2{\xi }^2}}$$
由此可知ξ越大 γ 越大σ%越小。
$$ts\omega c=\frac{7}{tan\gamma }$$
当确下γ和ts要求时候，可以求出ωc。从公式可以看出，γ一定时候ωc 越大，越小。

四、高频段
高频段原理系统截止频率，对系统动态性能影响很小，但从系统扛干扰能力上来说，高频段增益越低，下降斜率越大，系统抗高频干扰能力越强。

五，高阶系统
从以上分析来看，二阶系统通过幅频特性曲线来分析系统动态性能，没有时域分析来的简单直观，但高阶是系统即使用时域法降阶分析也挺麻烦，当然三阶以上的系统要求出频域的γ和ωc也不容易。因此我们的前人总结了如下经验近似公式，方便估算系统特性：
$$\begin{gathered} \sigma =[0.16+0.4(\frac{1}{sin\gamma }-1)](35°\le \gamma \le 90°) \\ ts=\frac{pi}{\omega c}[2+1.5(\frac{1}{sin\gamma }-1)+2.5(\frac{1}{sin\gamma }-1{)}^2]（35°\le \gamma \le 90°） \end{gathered}$$
当系统ωc一定时，γ增加， σ和ts都会下降。

最后

以上就是明理电源为你收集整理的从频域幅频曲线看系统性能的全部内容，希望文章能够帮你解决从频域幅频曲线看系统性能所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。