自动控制原理(一)

一阶系统

1.数学模型

系统闭环传递函数入下图:

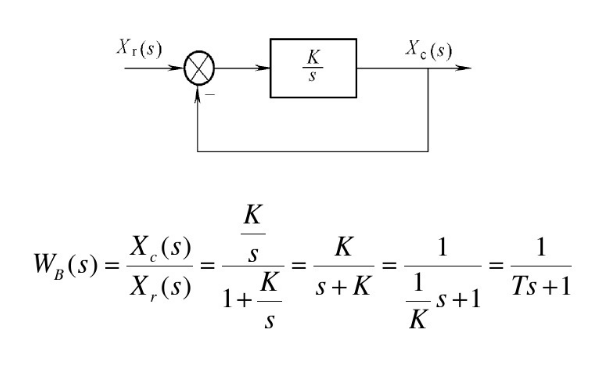
开环传函：积分环节
闭环传函：惯性环节

2.单位阶跃响应

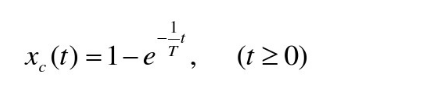
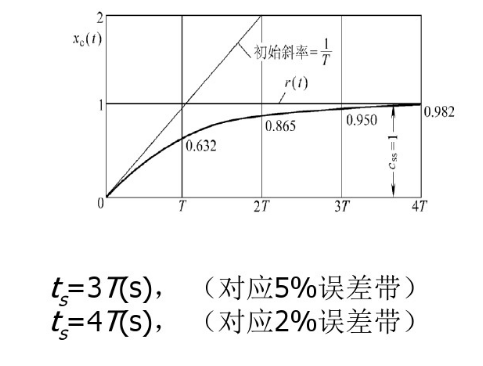
3.特性分析

• 1.一阶系统是稳定的，不会超调和震荡
• 2.一阶系统的稳态误差为0
• 3.一阶系统暂态特性也很好，系统响应速度正比于时间常数T的倒数，T越小响应越快

4.典型实例

位置闭环系统：

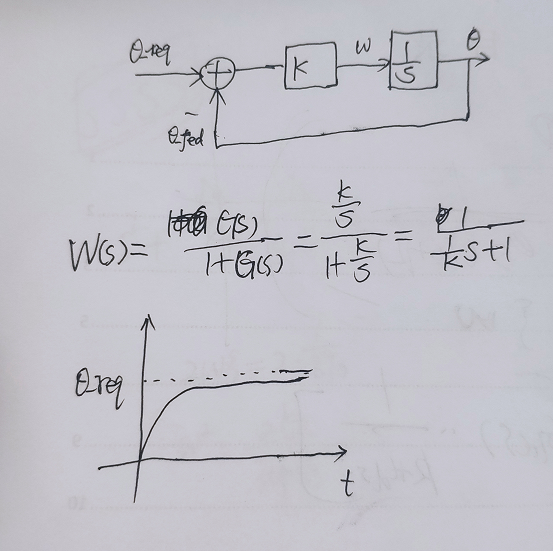
理论上k越大响应越快，但是k的上限还要收到执行机构的灵敏度的限制

二阶系统

1.数学模型

典型二阶系统:

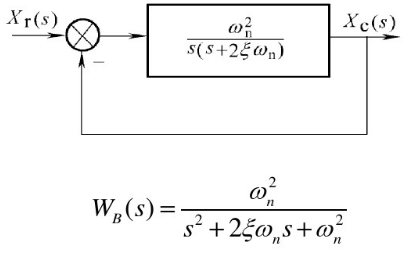
自然角频率: ${\omega }_n$
阻尼比:$\xi$
闭环传函：震荡环节

2.单位阶跃响应

• 1.过阻尼$\xi >1$
  阶跃响应的时域函数
  
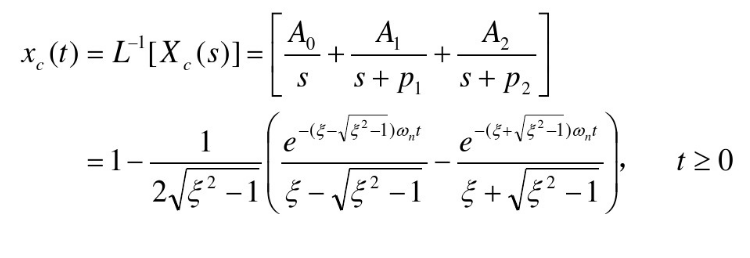
  结论：过阻尼时特征方程存在两个不同负实根，暂态响应类似于一阶系统的响应。

• 2.临界阻尼$\xi =1$
  阶跃响应的时域函数：
  
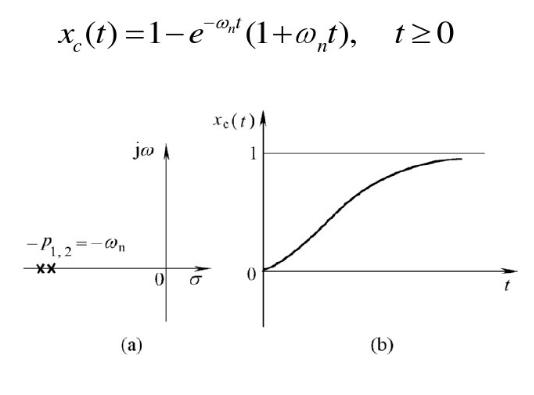
  结论：特征方程存在两个相同的负实根，系统不存在震荡，系统调节时间较长

• 3.欠阻尼$0<\xi <1$
  
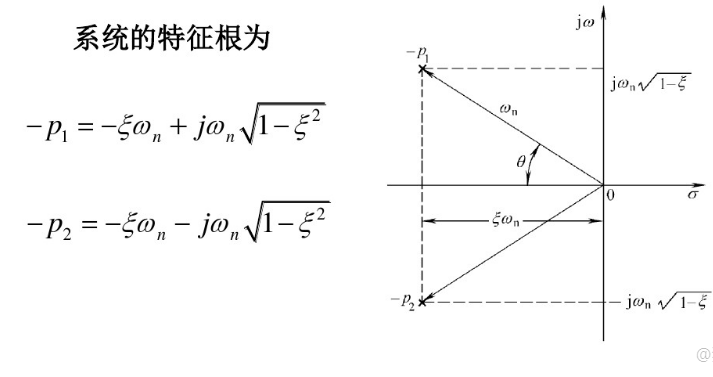
  时域函数：
  
  

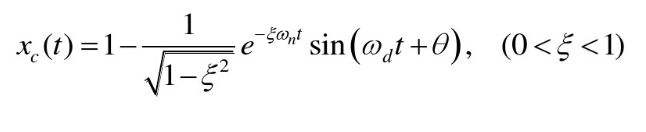
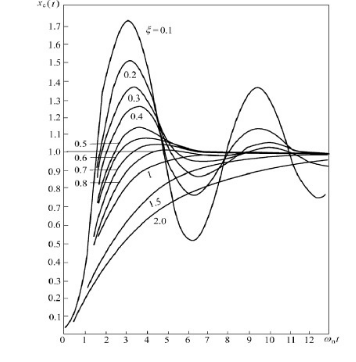
结论:欠阻尼时阶跃响应为指数衰减的简谐振动时间函数，$\xi$越小震荡越激烈

• 无阻尼$\xi =0$
  
  综上：对二阶系统来说，欠阻尼情况最具有实际意义。

3.暂态响应的定量分析指标

• 1.上升时间$t_r$:当${\omega }_n$一定时，$\xi$越小，上升越快；$\xi$一定时，${\omega }_n$越大，上升越快
• 2.调节时间$t_s$:近似与$\xi {\omega }_n$成反比关系，因此当$\xi$一定时，增大${\omega }_n$可以加快系统调节时间
• 3.最大超调量$\delta$%:只与阻尼比有关，$\xi$越小，超调量越大，通常根据允许的超调量来确定$\xi$
• 4.震荡次数$\mu$
• 5.二阶系统的工程最佳参数：$\xi =1/sqrt(2)$
  

以上只写出了最终结论，具体推算过程见参考资料。

高阶系统

1.首先极点要分布在虚轴左侧
2.高阶系统可以分解为若干个暂态分量的和，经过适当的舍去可将高阶系统近似降阶位一或二阶系统
3.选择主导极点，距离虚轴近，附近无零点，并且它的实部小于其他极点实部的1/5.如果这个极点是一对共轭极点，那么系统就可以近似的当作二阶系统来分析，并可以用二阶系统的性质来设计系统参数优化系统指标

自动控制系统稳定性

1.绝对稳定性：系统稳定的充要条件<=>闭环特征方程的极点全部在虚轴左侧
2.稳态误差：是系统控制精度的度量既与系统结构参数有关还和输入信号的形式大小和输入点有关
3.稳态误差和动态精度是互相矛盾的，可以通过1.增加校正 2.前馈补偿的方法来提高系统稳定精度

参考资料

自控原理教材

最后

以上就是坚强鞋子为你收集整理的自动控制原理(一)的全部内容，希望文章能够帮你解决自动控制原理(一)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。