一阶低通滤波器_一阶系统数学模型

叙述：   

所谓数学模型，就是根据系统运动过程规律，描述系统规律和特性，输入和输出关系的表达式。实际的系统比较复杂，甚至不清楚其内部机理。写出实际工程系统的数学模型是很困难的。下面介绍些简单系统，基于系统机理分析建立数学模型的基本方法。

系统稳定性，时域分析法：

稳定性是讨论系统没有输入和输入作用下的状态，故用零状态响应和阶跃响应的时域分析法来分析系统稳定性。

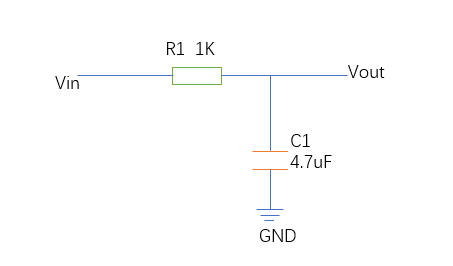
如图典型的RC电路直流，交流，信号都可以用，这就是个一阶系统。系统中含有一个动态元件C，这种电路(系统)用线性常系数一阶常微分方程来描述，所以称为一阶电路。

根据KVL建立动态方程：

电容电流：

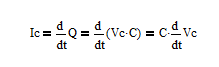
系统动态方程：  

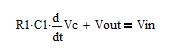令R1C1=Trc为电路时间常数解得：

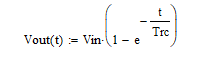
电压零状态响应：

在t=0时，Vout等于0，符合了电容电压不能突变的原理。

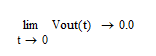
电压单位阶跃响应：

在t=∞时，Vout等于Vin(电源电压)

电压单位阶跃响应函数图像：

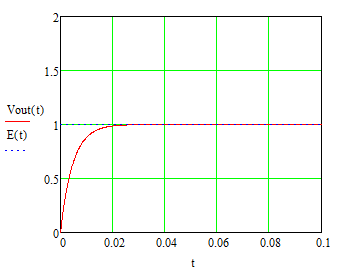
    电压阶跃响应函数图像：

从电压阶跃响应函数图像可以看出发生了变化，RC电路(系统)有突出恒定量，压低变化量的作用。

另一个角度和领域考虑：

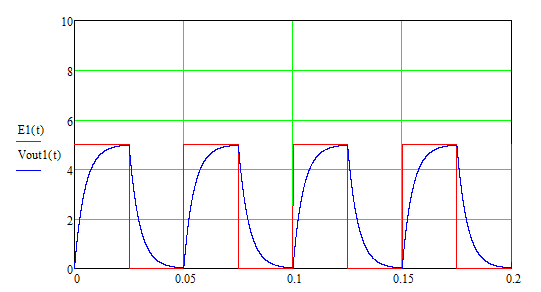
方波函数表达式和傅里叶展开式：

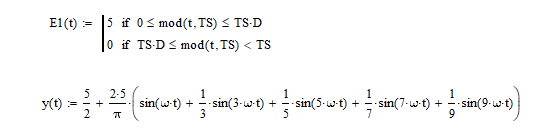
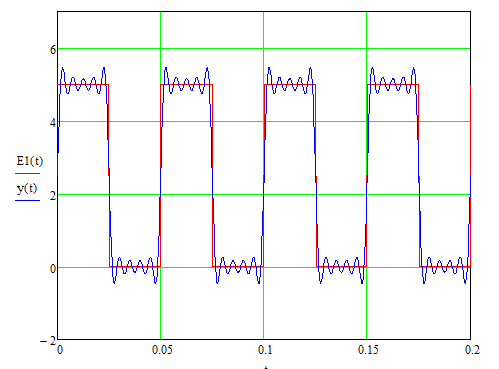
方波信号在时域中看起来是一个单纯周期信号，但是它的频谱分量却很丰富，实际上包括了许多高频信号，所以在经过RC后高频谐波分量被滤除，波形发生了变化。被称为一阶低通滤波器(LPF)。

系统稳定性，频域分析法：

时域分析法通过动态方程分析系统有很多不足，比如高阶系统微分方程求解困难。时间响应没有明确反映系统响应过程中结构，参数(谐波分量)之间的关系。频域分析一定程度上克服了时域分析的不足。

以电容电压为输出RC电路的传递函数，由于傅氏变换和拉氏变换是等价的频率特性与传递函数存在如下关系：

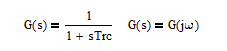
将传递函数的S替换jω得到频率特性：

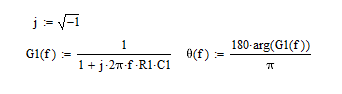频率特性一般为复变函数，所以表示为指数形式。G1(f)的模值称为幅频特性，φ(f)的幅角称为相频特性。

这里说明一般用对数表示增益G，电子技术做如下规定：

取对数的功率增益单位是B贝尔，B单位较大，常用分贝dB表示，故功率增益，电压增益，电流增益如下：

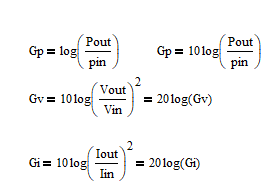
一阶低通滤波器(LPF)截止频率定义

当保持输入信号的幅值不变，通过改变输入信号频率，当出现输出信号降至输入信号幅值的0.707倍(-3dB)时，此时对应的频率称为这个滤波器的截止频率。

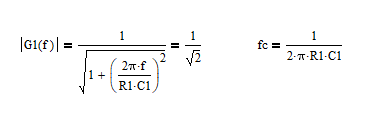
求值可以得到截止频率fc。

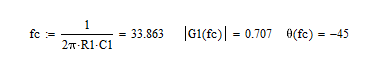
以频率和截止频率的比值参考绘制幅频特性，相频特性曲线也可以查到相关参数值。

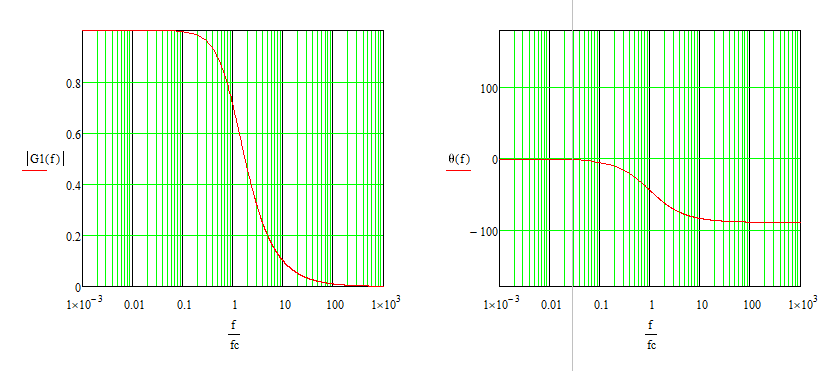
频率分析法得知：

f幅值相位是平行与横坐标的直线，基本没有衰减，滞后。

f=fc时，幅值衰减0.707倍，即-3dB。相位滞后45°。对于滤波器该频率称为截止频率。

f>>fc时, 幅值是斜率-20dB/十倍频成比例的一条直线衰减。相位随频率增加最终滞后90°。

频率特性的几何表示：

频率分析法是一种图解法，.主要有奈氏图，伯德图， 尼氏图。

伯德图是由对数幅频特性和对数相频特性组成：

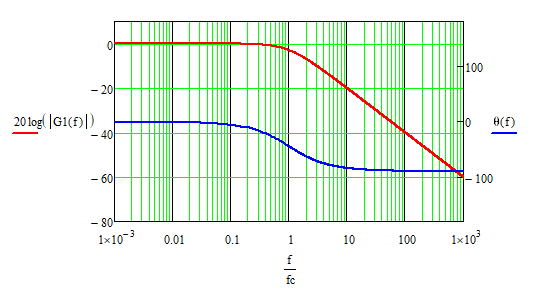
伯德图和传递函数得到RC 积分滤波电路的分母为零是极点电路,极点频率:fc=1/(2*π*R*C);频率低于极点频 率的信号保持与输入信号同样大小从输出端输出,即增益为 0dB,而频率高于极 点频率的信号则以-20dB/倍频下降,斜率-1。