matlab 最小二乘法拟合_模型参数预估 & 最小二乘法

160 阅读 0 评论 106 点赞

我是靠谱客的博主年轻悟空，这篇文章主要介绍matlab 最小二乘法拟合_模型参数预估 & 最小二乘法，现在分享给大家，希望可以做个参考。

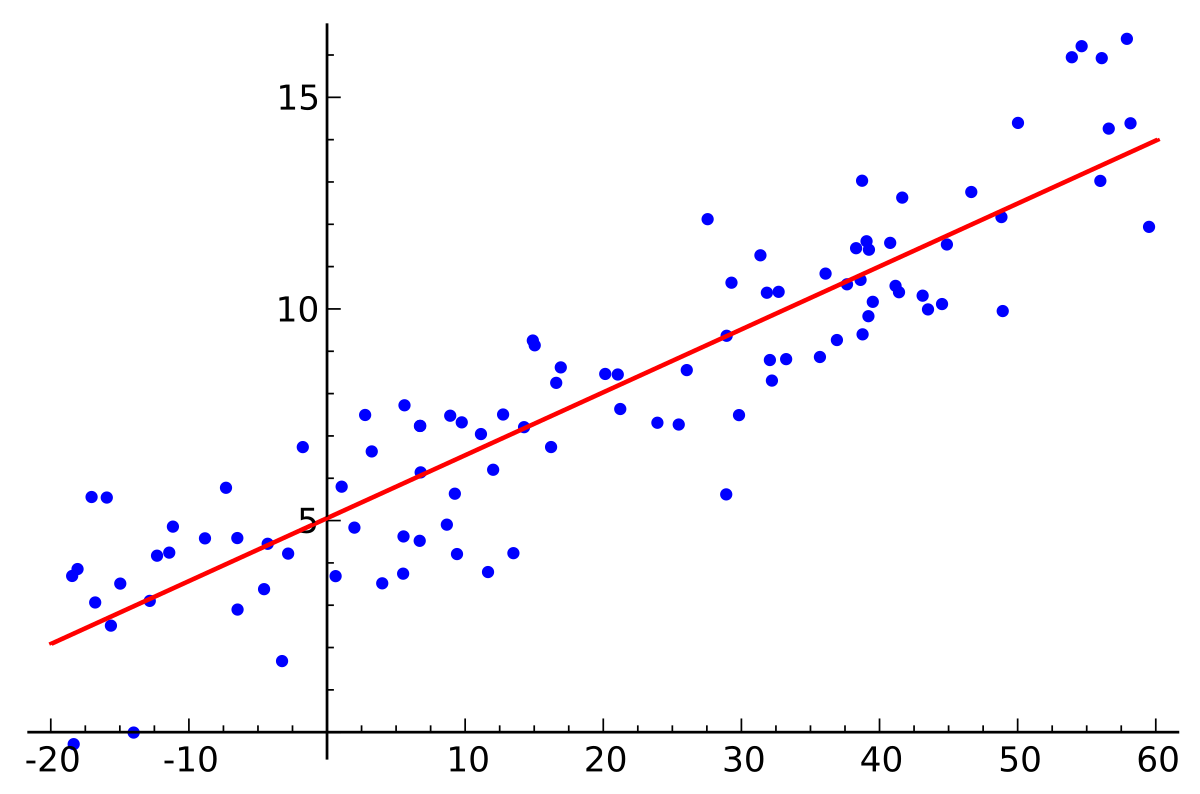
最小二乘法可以说是线性回归或者机器学习中最重要一个工具了。维基百科云：它通过最小化误差的平方和寻找数据的最佳函数匹配。这学期在上导师的新课 Estimation in Control。从预估的角度，我们来看看通过最小二乘法我们能做些什么用于模型的参数预估。

文章结构如下：

问题描述

假设我们有系统输入

，以及系统输出

。其中，输入和输出之间通过

来连接，其中

为我们要预估的模型参数。

如果我们假设我们的模型参数与输入为线性关系：

我们可以定义：

那么我们就有：

上面的这个模型不仅仅适用于线性时不变系统（LTI），还可以推广用来表示其他系统，例如：

线性时变系统：

这里我们可以定义：

非线性系统：

我们可以对应地定义：

只要我们的要预估的参数于系统输入成线性关系，都可以用式（1）来表示。

假设我们可以测量

组输入输出数据，即我们有

。我们的目标就是要找到最佳的系统模型参数

使得系统模型能够很好的匹配测得的数据。这里我们就可以用最小二乘法来解决参数预估的问题。

最小二乘法应用

预估模型参数可以通过最小二乘法来实现，首先我们可以定义用于评判模型参数优劣指标：残差（residual）—— 实际观察值与估计值之间的差：

最小二乘法通过最小化下面的目标函数来找到最优的模型参数：

上面的最优问题可以通过对

求导并令其一阶导数为0来得到最优解

如果我们定义：

我们可以得到：

如果

是一个满秩矩阵（即可逆），我们可以得到：

以上就是年轻悟空最近收集整理的关于matlab 最小二乘法拟合_模型参数预估 & 最小二乘法的全部内容，更多相关matlab内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。