基于Matalab的连续信号分析与离散信号分析

最近正在学习数字信号处理，由于后期可能会用到Matalab进行信号分析，所以将Matalab中一些重要的信号分析函数进行记录。

绘图函数：

进行线性绘图：plot(x,y,‘option’) or plot(x1,y1,‘option1’,x2,y2,‘option2’)
进行符号函数绘图：ezplot
进行离散序列绘图：stem
进行阶梯图绘图：stairs

数学运算：

微分运算：diff(function,‘variable’,n) 其中function是需要进行求导运算的函数，或是被赋值的符号表达式；variable为求导运算的独立变量；n为求导阶数。
积分运算：int(function,‘variable’,a,b) 其中function表示被积函数，或是被赋值的符号表达式；variable为积分变量；a为积分下限，b为积分上限

连续时间信号与系统时域分析：

常系数微分方程的符号求解：desolve(‘eq1,eq2,……’，‘cond1,cond2’，‘v’) 其中，参数eq1，eq2，……表示各微分方程，微分或导数的输入Dy，D2y，D3y来表示y的一阶导数，二阶导数，三阶导数，参数cond1,cond2表示各初始条件，参数v表示自变量，默认为变量t
零初始条件下微分方程的数值解：lsim（）函数
信号的冲击响应求解：impulse() 该函数将绘出由向量a，b表示的连续系统在指定时间范围内的冲激响应h(t)的时域波形图。
信号的阶跃响应求解：step()函数
信号卷积：conv(f1,f2)函数
傅里叶变换和傅里叶逆变换：fourier（）和 Ifourier（）函数

连续时间信号与系统复频域分析

拉式正反变化：laplace() 与ilaplace() 函数
复杂有理分式F(s)的部分分式展开式：[r,p,k]=residue(b,a)，其中，b，a分别表示F(s)的分子和分母多项式的系数向量；r为部分分式的系数；p为极点；k为F(s)中整式部分的系数，若F(s)为有理真分式，则k为0
计算分子和分母多项式根的函数：roots（）函数，可用于求解系统的零极点

离散系统的时域分析与Z域分析

求解离散系统的单位序列响应：h=impz（b，a，k） 其中b和a是由描述系统的差分方程的系数决定的表示离散系统的两个行向量，k表示输出序列的取值范围，h就是系统的单位序列响应。
求解离散系统时域响应：y=filter（b，a，f）用于计算系统在输入f作用下的零状态响应y
说明：离散系统的时域响应有两种求法：1.直接利用filter函数。2.利用impz函数求出差分方程的单位序列响应后利用conv函数与输入信号进行卷积。
Z变换和Z反变换：ztrans()和iztrans()函数
零极点分布图的绘制：zplane()函数，可在roots()函数后利用zplane()函数进行零极点分布图的绘制。
分析离散系统的频率特性：【H，w】=freqz(b,a,N)或freqz(b,a,N,‘whole’)函数 其中b和a分别是待分析的离散系统的系统函数分子和分母多项式的系数，N为正整数，返回向量H则包含了离散系统频率响应N个频率等分点的值，向量w则包含N个频率等分点。
说明：如果已知系统函数H（z），可以利用freaqz函数求出频率响应。
离散傅里叶快速算法FFT与FFT反变换：y=fft(x,n)和y=ifft(x,n)函数

实例

1.进行给定长度的连续信号傅里叶变换的数值计算
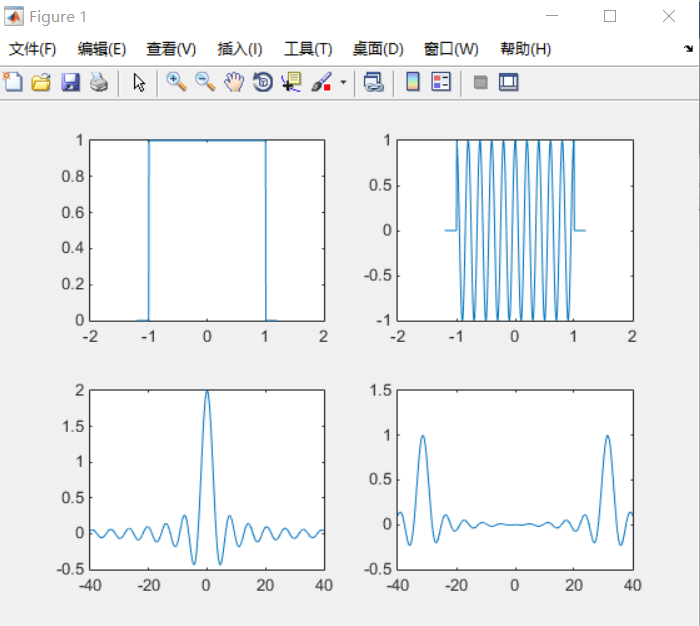
题目:进行f(t)和f1(t)的时域波形绘制和频谱绘制，并观察变换的频移特性

R=0.005;
t=-1.2:R:1.2;
f=Heaviside(t+1)-Heaviside(t-1);
f1=f.*cos(10*pi*t);
subplot(2,2,1)
plot(t,f)
subplot(2,2,2)
plot(t,f1)
W1=40;
N=1000;
k=-N:N;
W=k*W1/N;
F=f*exp(-j*t'*W)*R;
F=real(F);
F1=f1*exp(-j*t'*W)*R;
F1=real(F1);
subplot(2,2,3)
plot(W,F);
subplot(2,2,4);
plot(W,F1)

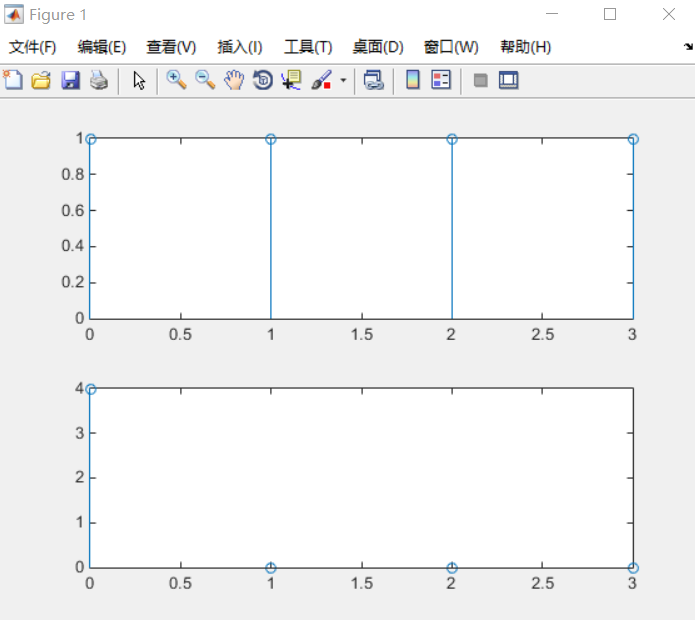
2.离散傅里叶变换
求解f(k)=G4(k)的DFT

N=4;
n=0:N-1;
Fn=[1 1 1 1];
k=0:N-1
WN=exp(-j*2*pi/N)
nk=n'*k;
WNnk=WN.^nk;
fk=Fn*WNnk
subplot(2,1,1)
stem(n,Fn)
subplot(2,1,2)
stem(k,abs(fk))

后期可能会补充一些内容

最后

以上就是缥缈银耳汤为你收集整理的基于Matalab的连续信号分析与离散信号分析的全部内容，希望文章能够帮你解决基于Matalab的连续信号分析与离散信号分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。