动态规划-避障道走法计算(AvoidRoads)

动态规划-避障道走法计算(AvoidRoads):

从右下坐标（0,0）出发，走到右上角的坐标。其中黑色粗体道路表示道路无法通行。只可以往右或上走，求走法可能。

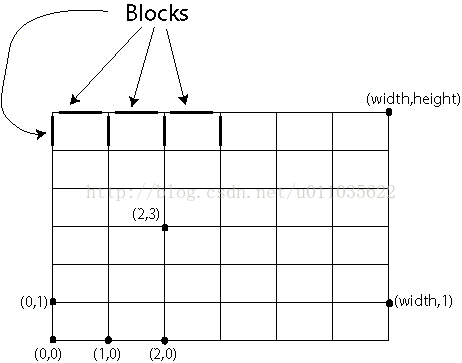
输入

width 

height

n

x1 y1 x2 y2

其中前两个数分别表示宽度和高度。

n表示不可通道路的数量。

x1 y1 x2 y2 表示从(x1,y1)到(x2,y2)的道路不可通。

示例：

width  = 6
length = 6
n = 2
0 0 0 1

6 6 5 6

Return ：252

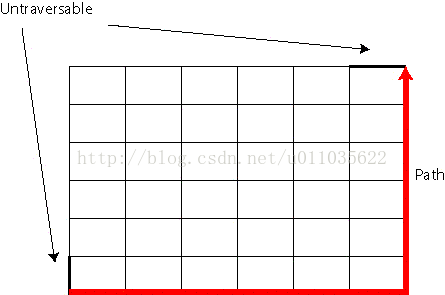
更多示例：

35
31

0
Returns: 6406484391866534976



2
2

3
{"0 0 1 0", "1 2 2 2", "1 1 2 1"}
Returns: 0

开始是用暴力搜索的方法，通过递归遍历全部，代码如下：

import java.util.Scanner;
import java.util.Arrays;
public class Main {
	static long count = 0;
	public static void findback(int x ,int y ,int mark[][]){
		System.out.println(count);
		if (x == mark.length-1 &&y == mark.length-1) {//已到达右上角终点的情况。
			count++;
			return;
		}
		if (mark[x][y] == 0) {	//两条路都可以走。
			if (x != mark.length-1) {//判断是否到达右边界
				findback(x+1,y,mark);
			}
			if (y != mark.length-1) {//判断是否到达上边界
				findback(x,y+1,mark);
			}
		}
		if (mark[x][y] == 5 && y != mark.length-1) {//右路封了，只能往上走，同时判断是否为上边界。
			findback(x,y+1,mark);
		}
		if (mark[x][y] == 3 && x != mark.length-1) {//上路封了，只能往右走，同时判断是否为右边界。
			findback(x+1,y,mark);
		}
	}
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int X = sc.nextInt()+1;
		int Y = sc.nextInt()+1;
		int side = Math.max(X, Y);
		int[][] mark = new int[side][side];
		int N = sc.nextInt();
		for (int i = 0; i < N; i++) {
			int x1 =sc.nextInt();
			int y1 =sc.nextInt();
			int x2 =sc.nextInt();
			int y2 =sc.nextInt();
			if (Math.abs(x2-x1) == 1) {
				int min = Math.min(x1, x2);
				mark[min][y1] = 5;//代表只能向上
			}
			if (Math.abs(y2-y1) == 1) {
				int min = Math.min(y1, y2);
				mark[x1][min] = 3;//代表只能向右
			}
		}
		for (int j = 0; j < mark.length; j++) {
			System.out.println(Arrays.toString(mark[j]));
		}
		findback(0,0,mark);
		System.out.println(count);
	}
}

后来发现这样的方法不行，因为数据较大时完全不行。（其实应该早点看出来的。。）

问了个比较懂算法的同学，理解了一下编写规律和方法。记录如下：

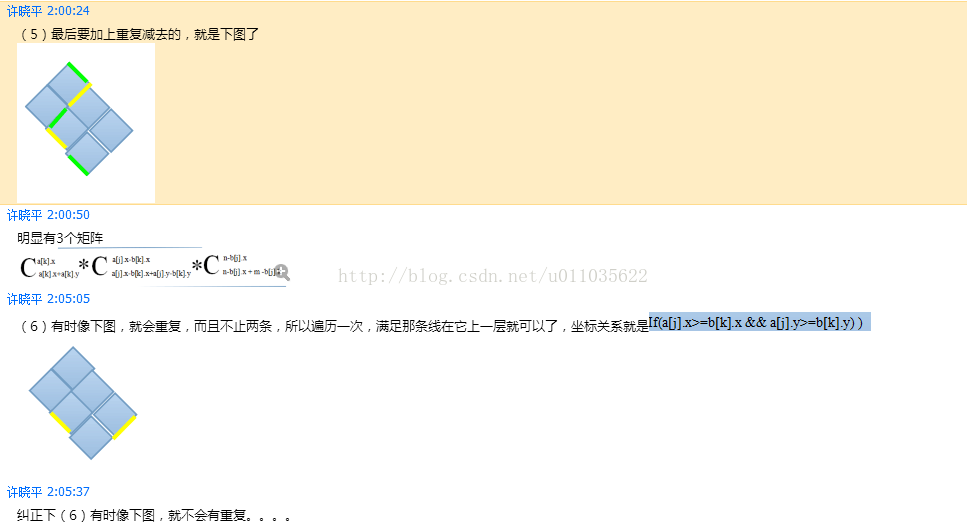
最后那几句话没怎么懂他在说什么，但是理解规律就大概知道该怎么编了~

代码如下：

import java.util.Scanner;

public class Main {
	//排列组合算法。十分容易溢出。
	public static Long C(Long X, Long Y) {
		Long output = 1l;
		for (Long i = X + Y; i > Y; i--) {
			output *= i;
			// System.out.println("1 parpered:"+output);
		}
		for (Long j = 1l; j <= X; j++) {
			output /= j;
			// System.out.println("2 parpered:"+output);
		}
		return output;
	}
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		Long X = sc.nextLong();
		Long Y = sc.nextLong();
		int N = sc.nextInt();
		Long[][] a = new Long[2][N];
		Long[][] b = new Long[2][N];
		for (int i = 0; i < N; i++) {
			Long x1 = sc.nextLong();
			Long y1 = sc.nextLong();
			Long x2 = sc.nextLong();
			Long y2 = sc.nextLong();
			a[0][i] = Math.min(x1, x2);//
			a[1][i] = Math.min(y1, y2);//
			b[0][i] = Math.max(x1, x2);//
			b[1][i] = Math.max(y1, y2);//
		}
		//从左下到右上的通路的走法总数（无阻碍通道的情况）。
		Long output = C(X, Y);
		System.out.println("first:" + output);
		
		//减去每条障碍通道所占有的通路可能 （相互之间会有重叠部分，所以后面要加回来。）
		for (int i = 0; i < N; i++) {
			output -= C(a[0][i], a[1][i]) * C(X - b[0][i], Y - b[1][i]);
		}
		System.out.println("second:" + output);
		
		//多减去的通路重叠那部分加回来（也就是交集的部分。）
		for (int i = 0; i < N; i++) {
			for (int j = i + 1; j < N; j++) {
				//类似冒泡的方法，让每两个阻碍道都有机会判断一次
				
				//因为输入的大小顺序没有确定，所以要分下面两种情况，其他情况不会产生交集。
				//目的是让右上的点减左下的点。
				
				// i点在j点右上方
				if ((a[0][i] >= b[0][j] && a[1][i] >= b[1][j])) {	
					output += C(Math.min(a[0][i], a[0][j]),
							Math.min(a[1][i], a[1][j]))
							* C(Math.abs(a[0][i] - b[0][j]),
									Math.abs(a[1][i] - b[1][j]))//<<==事实上两种情况只有这里不同（为了区分这个因数的情况）。
							* C(X - Math.max(b[0][j], b[0][i]),
									Y - Math.max(b[0][j], b[1][i]));
				}
				// j点在i点右上方
				if (((a[0][j] >= b[0][i] && a[1][j] >= b[1][i]))) {
					output += C(Math.min(a[0][i], a[0][j]),
							Math.min(a[1][i], a[1][j]))
							* C(Math.abs(a[0][j] - b[0][i]),
									Math.abs(a[1][j] - b[1][i]))//<<==事实上两种情况只有这里不同。
							* C(X - Math.max(b[0][j], b[0][i]),
									Y - Math.max(b[0][j], b[1][i]));
				}
				System.out.println("last parpered:" + output);
			}
		}
		System.out.println("last:" + output);
	}
}

最后

以上就是慈祥蜜蜂为你收集整理的动态规划-避障道走法计算(AvoidRoads)的全部内容，希望文章能够帮你解决动态规划-避障道走法计算(AvoidRoads)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。