matlab求系统根轨迹和系统增益,控制系统的根轨迹分析

一、根轨迹分析方法的概念

所谓根轨迹是指，当开环系统某一参数从零变到无穷大时，闭环系统特征方程的根在s平面上的轨迹。一般来说，这一参数选作开环系统的增益K，而在无零极点对消时，闭环系统特征方程的根就是闭环传递函数的极点。

根轨迹分析方法是分析和设计线性定常控制系统的图解方法，使用十分简便。利用它可以对系统进行各种性能分析，

１．稳定性

当开环增益K从零到无穷大变化时，图中的根轨迹不会越过虚轴进入右半s平面，因此这个系统对所有的K值都是稳定的。如果根轨迹越过虚轴进入右半s平面，则其交点的K值就是临界稳定开环增益。

２．稳态性能

开环系统在坐标原点有一个极点，因此根轨迹上的K值就是静态速度误差系数，如果给定系统的稳态误差要求，则可由根轨迹确定闭环极点容许的范围。

３．动态性能

当00.5时，闭环极点为复数极点，系统为欠阻尼系统，单位阶跃响应为阻尼振荡过程，且超调量与K成正比。

例exp4_18．m

%exp4_18．m

%对根轨迹进行分析

%二阶开环系统为H(s)=K/(s*(0.5s+1))

clear

closeall

clc

num=1;

den=[0.510];

rlocus(num,den);

text(0.1,0.1,'k=0');

text(-0.9,0.1,'k=0.5');

二、根轨迹分析函数

通常来说，绘制系统的根轨迹是很繁琐的事情，因此在教科书中介绍的是一种按照一定规则进行绘制的概略根轨迹。在MATLAB中，专门提供了绘制根轨迹的有关函数。

pzmap：绘制线性系统的零极点图

rlocus：求系统根轨迹。

rlocfind：计算给定一组根的根轨迹增益。

sgrid：在连续系统根轨迹图和零极点图中绘制出阻尼系数和自然频率栅格。

(一)零极点图绘制

MATLAB提供了函数pzmap()来绘制系统的零极点图，其用法如下：

[p,z]=pzmap(a,b,c,d)：返回状态空间描述系统的极点矢量和零点矢量，而不在屏幕上绘制出零极点图。

[p,z]=pzmap(num,den)：返回传递函数描述系统的极点矢量和零点矢量，而不在屏幕上绘制出零极点图。

pzmap(a,b,c,d)或pzmap(num,den)：不带输出参数项，则直接在s复平面上绘制出系统对应的零极点位置，极点用×表示，零点用o表示。

pzmap(p,z)：根据系统已知的零极点列向量或行向量直接在s复平面上绘制出对应的零极点位置，极点用×表示，零点用o表示。

exp4_19．m

%零极点图的绘制

clc

clear

closeall

%已知系统的状态空间描述模型

a=[03;-3-1];

b=[01]';

c=[13];d=2;

[p1,z1]=pzmap(a,b,c,d)

subplot(221)

pzmap(p1,z1)

subplot(222)

pzmap(a,b,c,d)

%已知系统传递函数模型

num=[2255110];

den=[11577840];

[p2,z2]=pzmap(num,den)

subplot(223)

pzmap(p2,z2)

subplot(224)

num1=[24];

den1=[8831];

pzmap(num1,den1)

moreoff

(二)根轨迹图绘制

MATLAB提供了函数rlocus()来绘制系统的根轨迹图，其用法如下：

rlocus(a,b,c,d)或者rlocus(num,den)：根据SISO开环系统的状态空间描述模型和传递函数模型，直接在屏幕上绘制出系统的根轨迹图。开环增益的值从零到无穷大变化。

rlocus(a,b,c,d,k)或rlocus(num,den,k)：通过指定开环增益k的变化范围来绘制系统的根轨迹图。

r=rlocus(num,den,k)或者[r,k]=rlocus(num,den)：不在屏幕上直接绘出系统的根轨迹图，而根据开环增益变化矢量k，返回闭环系统特征方程1＋k*num(s)/den(s)=0的根r，它有length(k)行，length(den)-1列，每行对应某个k值时的所有闭环极点。或者同时返回k与r。

若给出传递函数描述系统的分子项num为负，则利用rlocus函数绘制的是系统的零度根轨迹。(正反馈系统或非最小相位系统)

exp4_20．m

%根轨迹图的绘制

clc

clear

closeall

%已知系统的状态空间描述模型

a=[03;-3-1];

b=[01]';

c=[13];d=2;

subplot(211)

rlocus(a,b,c,d)

%已知系统传递函数模型

num=[24];

den=[8310];

subplot(212)

rlocus(num,den)

[r,k]=rlocus(num,den);

disp('r的维数')

size(r)

(三)rlocfind()函数

MATLAB提供了函数rlocfind()来找出给定的一组根(闭环极点)对应的根轨迹增益。其用法如下：

[k,p]=rlocfind(a,b,c,d)或者[k,p]=rlocfind(num,den)

它要求在屏幕上先已经绘制好有关的根轨迹图。然后，此命令将产生一个光标以用来选择希望的闭环极点。命令执行结果：k为对应选择点处根轨迹开环增益；p为此点处的系统闭环特征根。

不带输出参数项[k,p]时，同样可以执行，只是此时只将k的值返回到缺省变量ans中。

(四)sgrid()函数

sgrid：在现存的屏幕根轨迹或零极点图上绘制出自然振荡频率wn阻尼比矢量z对应的格线。

sgrid(‘new’)：是先清屏，再画格线。

sgrid(z,wn)：则绘制由用户指定的阻尼比矢量z自然振荡频率wn的格线。

三、根轨迹分析应用实例

例exp4_21．m　　已知某单位反馈系统的开环传递函数为：

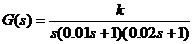
要求：绘制系统的闭环根轨迹，并确定使系统产生重实根和纯虚根的开环增益k。

%根轨迹图的绘制

clc

clear

closeall

%已知系统开环传递函数模型

num=1;

den=conv([0．0110],[0．021]);

rlocus(num,den)

[k1,p]=rlocfind(num,den)

[k2,p]=rlocfind(num,den)

title('rootlocus')

例exp4_22．m某开环系统传递函数如下所示：要求绘制系统的闭环根轨迹，分析其稳定性，并绘制出当k=55和k=56时系统的闭环冲激响应。

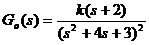
%根轨迹图的绘制与分析

clc

clear

closeall

%已知系统传递函数模型

numo=[12];

den=[143];

deno=conv(den,den);

figure(1)

k=0:0.1:150;

rlocus(numo,deno,k)

title('rootlocus')

[p,z]=pzmap(numo,deno);

%求出系统临界稳定增益

[k,p1]=rlocfind(numo,deno);

k

%验证系统的稳定性

figure(2)

subplot(211)

k=55;

num2=k*[12];

den=[143];

den2=conv(den,den);

[numc,denc]=cloop(num2,den2,-1);

impulse(numc,denc)

title('impulseresponsek=55');

subplot(212)

k=56;

num3=k*[12];

den=[143];

den3=conv(den,den);

[numcc,dencc]=cloop(num3,den3,-1);

impulse(numcc,dencc)

title('impulseresponsek=56');