Matlab: 传递函数的级联合成和分解1. 如何求级联系统的传递函数？2. 如何分解一个高阶传递函数为多个低阶传递函数？

74 阅读 0 评论 49 点赞

我是靠谱客的博主单身白猫，最近开发中收集的这篇文章主要介绍Matlab: 传递函数的级联合成和分解1. 如何求级联系统的传递函数？2. 如何分解一个高阶传递函数为多个低阶传递函数？，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1. 如何求级联系统的传递函数？

2. 如何分解一个高阶传递函数为多个低阶传递函数？

1. 如何求级联系统的传递函数？

已知一个级联系统的各级的传递函数，如何求整个级联系统的传递函数呢？

利用Matlab的tf()函数可以很简单地得到一个级联系统的传递函数，以下以一个简单的两级系统为例，直接看代码：

close all; clear; clc

b1 = [1.0000   -1.9981  0.9983];
a1 = [1.0000   -1.      0.9];

b2 = [1.0000   -0.9981  0.99];
a2 = [1.0000   -0.5     0.9];

% b12 = conv(b0(1,:), b0(2,:))
% a12 = conv(a0(1,:), b0(2,:))

tf1  = tf(b1, a1)
tf2  = tf(b2, a2)
tf12 = tf1 * tf2
b12  = tf12.Numerator{1};
a12  = tf12.Denominator{1};


[H1 , W1 ] = freqz(b1 , a1 , 512); hold on;
[H2 , W2 ] = freqz(b2 , a2 , 512);
[H12, W12] = freqz(b12, a12, 512);
figure; 
plot(W1 , abs(H1 ),'b-'); hold on;
plot(W2 , abs(H2 ),'k-'); 
plot(W12, abs(H12),'r-'); 
legend('filter#1 frequence response', 'filter#2 frequence response', 'combined filter frequence response');

运行以上脚本可以得到如下结果，Matlab给出的分式表达式非常nice, user-friendly：

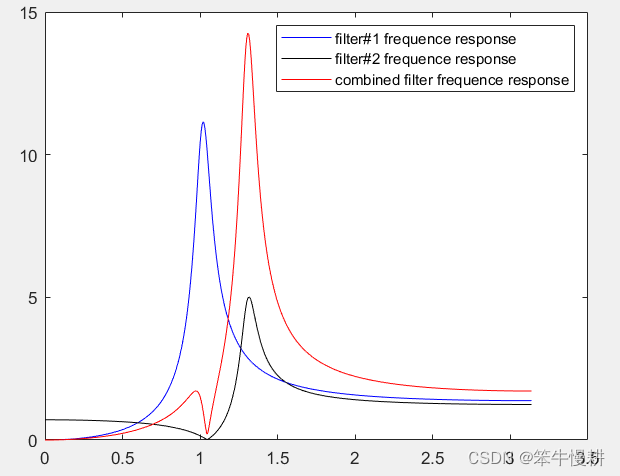
当然，以上是比较秀的写法，其实如上所示，级联系统的传递函数就是各级子系统的传递函数的乘积。因此级联系统的传递函数的分子和分母也可以分别以如下方式（土一点但是更加直观易懂）求得：

b12_2 = conv(b1, b2)
a12_2 = conv(a1, a2)

其中用到了conv()函数来计算两个多项式的乘积，更多的Matlab的多项式运算相关可以参考Matlab: 多项式表示及其基本运算。

如何更直观地验证以上合成系统和级联系统的等价性呢？可以做一个针对随机数序列的仿真。如下所示：

% Test the equivalence of the cascaded system and the combined system
N   = 1000;
x   = wgn(1000,1,1);    % 生成高斯白噪声
y1  = filter(b1,a1,x);  % 第一级滤波
y2  = filter(b2,a2,y1); % 第二级滤波

y12 = filter(b12,a12,x); % 合成系统滤波

fprintf(1,'The maximum absolute difference = %gn',max(abs(y2-y12)));

figure;
plot(y2); hold on;
plot(y12);
plot(y2-y12,'ko-');
legend('cascaded system output', 'combined filter output', 'difference');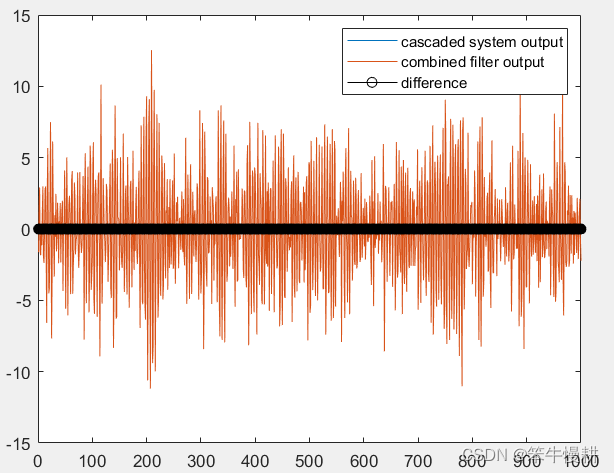

The maximum absolute difference = 6.81677e-14

忽略数值计算的误差的话，可以认为两个系统是完全等价的了。

2. 如何分解一个高阶传递函数为多个低阶传递函数？

由于级联系统的传递函数就是各级传递函数的乘积，将一个高阶传递函数分解为多个低阶传递函数的过程其实很直观。

step1：对传递函数的分子和分母分别进行因式分解，等价地来说就是求零点和极点。求得了各零点也就得到传递函数分子的各1阶因式。同理求得了各极点也就得到传递函数分母的各1阶因式。
step2：将分子的各1阶因式和分母的各1阶因式分别进行自由组合（当然每个因式只能用一次）可以得到组成级联系统的中的各级1阶子系统。
step3：如果需要更高阶的子系统（常用的是2阶子系统）的话，将两个1阶子系统按照第一节所述方法合成即可。

关于如何求零点和极点，可以使用matlab中的roots函数。也可以参考：Matlab/Simulink：动态系统模型的表示及仿真分析基础

当然，有Matlab提供的工具函数，就省掉了自己去分解并进行组合的麻烦了。最常见的IIR滤波器的实现是二阶IIR滤波器，通常称为bi-quadratic iir。Matlab提供了tf2sos()将高阶的iir滤波器分解为二阶IIR滤波器的级联实现，称为SOS IIR滤波器。

以下示例代码先用butter()函数生成了一个8阶巴特沃斯滤波器，然后利用tf2sos将其分解为4级SOS实现形式。最后将分解后的各级传递函数再合成，确认它与原滤波器的传递函数的确是相等的。

close all; clear; clc

[nm,dn] = butter(8,0.5)
[sos_matrix,gn] = tf2sos(nm,dn)

combined_num = conv(conv(sos_matrix(1,1:3),sos_matrix(2,1:3)),conv(sos_matrix(3,1:3),sos_matrix(4,1:3)));
combined_num = combined_num * gn
combined_den = conv(conv(sos_matrix(1,4:6),sos_matrix(2,4:6)),conv(sos_matrix(3,4:6),sos_matrix(4,4:6)))

运行结果如下：

nm = 0.0093 0.0741 0.2595 0.5190 0.6487 0.5190 0.2595 0.0741 0.0093

dn = 1.0000 -0.0000 1.0609 -0.0000 0.2909 -0.0000 0.0204 -0.0000 0.0002

sos_matrix =

1.0000 2.0003 0.9999 1.0000 -0.0000 0.0097
1.0000 2.0305 1.0309 1.0000 -0.0000 0.0920
1.0000 1.9997 1.0001 1.0000 -0.0000 0.2857
1.0000 1.9695 0.9700 1.0000 0.0000 0.6735

gn = 0.0093

combined_num = 0.0093 0.0741 0.2595 0.5190 0.6487 0.5190 0.2595 0.0741 0.0093

combined_den = 1.0000 -0.0000 1.0609 -0.0000 0.2909 -0.0000 0.0204 -0.0000 0.0002