matlab 最小二乘法拟合_最小二乘法辨识1阶离散传递函数

95 阅读 0 评论 63 点赞

我是靠谱客的博主敏感诺言，这篇文章主要介绍matlab 最小二乘法拟合_最小二乘法辨识1阶离散传递函数，现在分享给大家，希望可以做个参考。

一、摘要

本文使用最小二乘法，辨识传递函数的基本参数。

二、基本概念

1.最小二乘法

关键：计算出拟合点和实际点的距离的平方和，找到理想拟合曲线的参数。

应用：对于控制系统的辨识中，方便我们使用差分方程离散化传递函数，进行各参数的辨识。

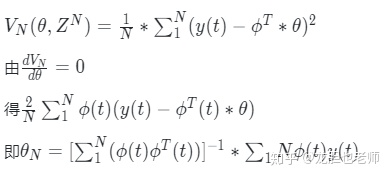
2.传递函数离散化

关键：使用一阶向后法，使得传递函数从s域转换到z域上。

公式：

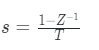
例子：

在matlab创建一个连续传递函数 Gs = tf([1],[2 1]) 离散化，用Gz = c2d(Gs,0.01)。其中0.01为离散采样时间

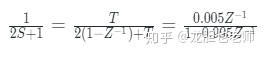
三、代码及结果验证

%尝试手写最小二乘法

%生成伪随机二值信号
Range = [-2,2];
Band = [0 1];
u1 = idinput([63,1,3],'prbs',Band,Range);
u1(:,1) = 1;
title('Periodic Signal')
%搭建一阶系统
sys = tf([1],[5 2]);
sysdiscrete = c2d(sys,0.01);
t = 0:0.01:1.88;
%获取输入输出数据
y1 = lsim(sys,u1,t);
%A
A=zeros(2);%2*2矩阵
for i = 1:188
    A(1,1) = A(1,1) + y1(i,1)^2;
    A(2,2) = A(2,2) + u1(i,1)^2;
    A(1,2) = A(1,2) - y1(i,1) * u1(i,1);
end
A(2,1) = A(1,2);
%B
B = [0;0];%2*1矩阵
for i = 1 : 188
    B(1,1) = B(1,1) -y1(i,1) * y1(i+1,1);
    B(2,1) = B(2,1) + u1(i,1) * y1(i+1,1);
end
%合并
C = inv(A) * B;