光伏-储能并网系统仿真(MATLAB/SIMULINK)-part1
如果不想看原理,可以直接点击文件下载连接
本文介绍如何利用MATLAB/SIMULINK完成一个光伏-储能并网系统的搭建。
一篇文章就能读懂光伏并网系统的控制,以及PI控制器的设计方法。
本文将会介绍四个部分:
- 整体系统控制逻辑
- 光伏并网逆变器的控制理论(dq解耦控制)
- 光伏MPPT控制以及恒功率控制
- 电池的功率控制
每个部分都会包括:
- 控制器原理
- PI控制器参数理论计算
1. 整体系统控制逻辑
1.1 系统要求
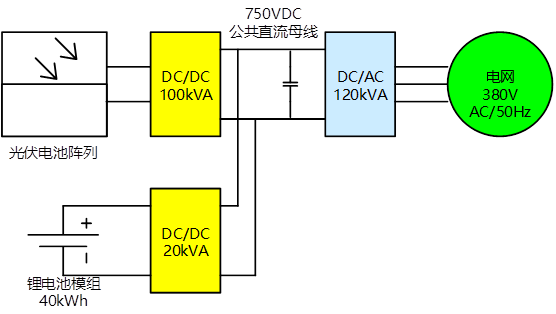
- 储能DC/DC变换器与光伏DC/DC变换器共直流母线(母线电压750V)运行,母线电压纹波需要小于5%。
- 储能电池系统双向功率控制,达到平滑系统功率输出的目的
1.2 系统控制方法
该系统需要考虑了两种场景分别是:
- 场景一:电池SOC较为健康(40%-90%),此时可以帮助平抑光伏的功率波动
- 场景二:电池SOC过低或者过高,此时电池需要恒功率的充电或者放电,以保护电池
针对这两种场景,系统需要采取不同的控制方式。
对于场景一,按照表1所示的控制方式可以实现系统有功输出和无功输出都保持恒定,从而可以满足系统的要求。
对于场景二,按照表1所示的控制方式,进行光伏弃光(即恒功率控制),同时对电池进行恒功率充电或者放电以保持系统总功率输出不变。
| 场景 | 光伏模块 | 电池 | 逆变器 |
|---|---|---|---|
| 场景一(电池SOC健康) | MPPT | 输出系统有功输出和光伏功率输出的差值 | 控制母线电压+控制无功输出 |
| 场景二 | 恒功率控制 | SOC过低(高):恒功率充(放)电 | 控制母线电压+控制无功输出 |
1.3 系统控制原理解释
控制的基本原理是:维持母线电容电压的稳定等价于光伏输出功率加上电池输出功率(充电记为负功率)与逆变器输出功率平衡。
如果记光伏出力为
P
1
P_1
P1,电池出力为
P
2
P_2
P2,逆变器出力为
P
3
P_3
P3。母线电压稳定就意味着电容的能量保持稳定,因此有如下关系:
P
1
+
P
2
=
P
3
P_1+P_2=P_3
P1+P2=P3
为了更清晰地解释,我们假设系统运行在场景一下。此时,光伏采用MPPT控制,因此光照和温度的变化都会引起光伏出力(
P
1
P_1
P1)的变化。假设系统要求出力为
P
∗
P^*
P∗,那么应该控制电池输出功率为
P
2
P_2
P2(
P
2
=
P
∗
−
P
1
P_2=P^*-P_1
P2=P∗−P1)。又因为逆变器控制了母线电压稳定,因此整个系统的输出就是
P
3
P_3
P3(
P
3
=
P
1
+
P
2
=
P
∗
P_3=P_1+P_2=P^*
P3=P1+P2=P∗)。因此也就满足了系统处理要求。
2. 光伏并网逆变器的控制理论(dq解耦控制)
2.1 逆变器有功无功控制
逆变器与电网的连接可以用如下公式近似表示:
U
a
b
c
=
i
a
b
c
R
+
L
d
i
a
b
c
d
t
+
e
a
b
c
(
1
)
U_{abc}=i_{abc}R+Lfrac{di_{abc}}{dt}+e_{abc} (1)
Uabc=iabcR+Ldtdiabc+eabc(1)
其中,下表abc表示abc三相所对应量所构成的列向量;
U
a
b
c
U_{abc}
Uabc表示逆变器的电压;
i
a
b
c
i_{abc}
iabc表示三相电流;
e
a
b
c
e_{abc}
eabc表示网侧的三相电压。
对公式(1)进行park变换,可以得到如下的公式:
{
v
d
=
R
i
d
+
L
d
i
d
d
t
−
ω
L
i
q
+
e
d
v
q
=
R
i
q
+
L
d
i
q
d
t
+
ω
L
i
d
+
e
q
(
2
)
left{ begin{array}{c} v_d=Ri_d+Lfrac{di_d}{dt}-omega Li_q +e_d \ v_q=Ri_q+Lfrac{di_q}{dt}+omega Li_d +e_q end{array} right. (2)
{vd=Rid+Ldtdid−ωLiq+edvq=Riq+Ldtdiq+ωLid+eq(2)
其中,
ω
omega
ω为park变化中dq坐标系的旋转角速度(一般选取为电网的频率)。(park变换的相关知识见文章park变换是什么?)
经过变换后,输出给电网的有功功率和无功功率可以表示为如下公式:
{
P
=
3
2
(
e
d
i
d
+
e
q
i
q
)
Q
=
3
2
(
e
q
i
d
−
e
d
i
q
)
(
3
)
left{begin{array}{c} P = frac{3}{2}(e_di_d+e_qi_q) \ Q=frac{3}{2}(e_qi_d-e_di_q) end{array}right. (3)
{P=23(edid+eqiq)Q=23(eqid−ediq)(3)
其中,P,Q分别代表输出给电网的有功和无功功率。
更进一步,在进行park变换时可以定义电网侧的电压矢量与d轴平行。(所谓的电压矢量与d轴平行其实就是在进行park变换时,通过调整变换矩阵的相位使得
e
q
=
0
e_q=0
eq=0)。因此,我们可以看到当
e
q
=
0
e_q=0
eq=0时,上面的功率的公式变成了更加简单的形式:
{
P
=
3
2
(
e
d
i
d
)
Q
=
3
2
(
−
e
d
i
q
)
(
4
)
left{begin{array}{c} P = frac{3}{2}(e_di_d) \ Q=frac{3}{2}(-e_di_q) end{array}right. (4)
{P=23(edid)Q=23(−ediq)(4)
上面的公式也就是常说的q轴电流控制无功,d轴电流控制有功。(但其实如果令电压矢量与q轴平行,不就是q轴电流控制有功了? ???? )
那么该如何控制dq轴电流呢?下面介绍电流环的设计思路和流程。
假设id和iq的参考值(
i
d
∗
,
i
q
∗
i_d^*,i_q^*
id∗,iq∗)已知,那么我们可以通过控制逆变器的电压输出使得
i
d
=
i
d
∗
,
i
q
=
i
q
∗
i_d=i_d^*,i_q=i_q^*
id=id∗,iq=iq∗。
首先,对公式(2)进行laplace变换:
{
i
d
=
V
d
+
ω
L
i
q
−
e
d
R
+
L
s
i
q
=
V
q
−
ω
L
i
d
−
e
q
R
+
L
s
(
5
)
left{ begin{array}{c} i_d=dfrac{V_d+omega Li_q-e_d}{R+Ls} \ i_q=dfrac{V_q-omega Li_d-e_q}{R+Ls} end{array} right. (5)
⎩⎪⎨⎪⎧id=R+LsVd+ωLiq−ediq=R+LsVq−ωLid−eq(5)其中,s为Laplace算子。
V
d
V_d
Vd和
V
q
V_q
Vq是逆变器的dq电压,因此这两个量是我们可以控制的。如果我们采取的是PI控制器,那么我们可以令这两个控制量为如下形式:
{
V
d
=
e
d
−
ω
L
i
q
+
(
K
p
+
K
i
/
s
)
(
i
d
∗
−
i
d
)
V
q
=
e
q
+
ω
L
i
d
+
(
K
p
+
K
i
/
s
)
(
i
q
∗
−
i
q
)
(
6
)
left{ begin{array}{c} V_d=e_d-omega Li_q+(K_p+K_i/s)(i_d^*-i_d) \ V_q=e_q+omega Li_d+(K_p+K_i/s)(i_q^*-i_q) end{array} right. (6)
{Vd=ed−ωLiq+(Kp+Ki/s)(id∗−id)Vq=eq+ωLid+(Kp+Ki/s)(iq∗−iq)(6)
将(6)带入(5),我们就可以整理得到如下的等式:
{
i
d
=
K
p
L
s
+
K
i
L
s
2
+
(
R
+
K
p
L
)
s
+
K
i
L
i
d
∗
i
q
=
K
p
L
s
+
K
i
L
s
2
+
(
R
+
K
p
L
)
s
+
K
i
L
i
q
∗
(
7
)
left{ begin{array}{c} i_d = dfrac{dfrac{K_p}{L}s+dfrac{K_i}{L}}{s^2+(dfrac{R+K_p}{L})s+dfrac{K_i}{L}}i_d^*\ i_q = dfrac{dfrac{K_p}{L}s+dfrac{K_i}{L}}{s^2+(dfrac{R+K_p}{L})s+dfrac{K_i}{L}}i_q^* end{array} right. (7)
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧id=s2+(LR+Kp)s+LKiLKps+LKiid∗iq=s2+(LR+Kp)s+LKiLKps+LKiiq∗(7)
式(7)表明如果我们确实可以让控制变量满足式(6)所示的关系,那么整个系统就可以表示为式(7)所示的一个二阶系统。并且我们可以看到如果
i
d
∗
i_d^*
id∗是一个阶跃信号,那么利用Laplace的终值定理可以得到如下关系:
lim
t
→
∞
i
d
(
t
)
=
lim
s
→
0
K
p
L
s
+
K
i
L
s
2
+
(
R
+
K
p
L
)
s
+
K
i
L
i
d
∗
s
∗
s
=
i
d
∗
(
8
)
lim_{trightarrow infty} i_d(t) = lim_{srightarrow 0}dfrac{dfrac{K_p}{L}s+dfrac{K_i}{L}}{s^2+(dfrac{R+K_p}{L})s+dfrac{K_i}{L}}dfrac{i_d^*}{s}*s=i_d^*(8)
t→∞limid(t)=s→0lims2+(LR+Kp)s+LKiLKps+LKisid∗∗s=id∗(8)
这也就意味着随着时间的推移,
i
d
i_d
id就会趋向于我们设定的
i
d
∗
i_d^*
id∗。
可是,我们往往不希望需要等到海枯石烂才能趋向于我们设定的值,因此我们还需要对PI控制器参数进行合理的配置,才能让式(7)所示的二阶系统具有足够好的动态要求。(合理的超调量和满足要求的收敛时间)
配置的方式有很多,这里介绍一种。
我们可以写出二阶系统所对应的阻尼系数和自由振荡频率,并且我们可以规定我们所期望的系统收敛时间
t
r
t_r
tr:
{
ξ
=
R
+
K
p
2
K
i
L
=
0.8
ω
n
=
K
i
L
=
3
ξ
t
r
t
r
=
0.01
(
9
)
left{ begin{array}{c} xi = frac{R+K_p}{2sqrt{K_iL}}=0.8\ omega_n=sqrt{frac{K_i}{L}}=frac{3}{xi t_r}\ t_r = 0.01 end{array} right. (9)
⎩⎪⎨⎪⎧ξ=2KiLR+Kp=0.8ωn=LKi=ξtr3tr=0.01(9)上面我们设定了系统的收敛时间为
t
r
=
0.01
s
t_r=0.01s
tr=0.01s,阻尼系数为0.8。两个方程以及两个未知数(
K
p
,
K
i
K_p,K_i
Kp,Ki),我们利用式(9)不难求得合适的PI参数值。
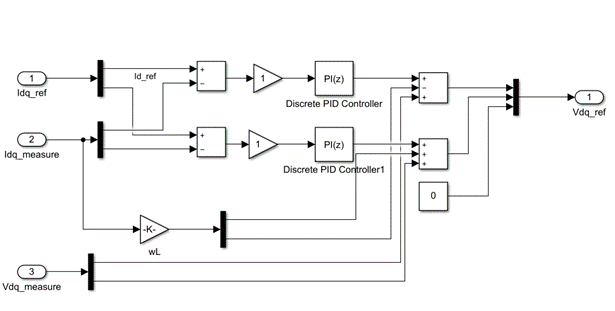
以上内容解决了电流环的设计问题,那么剩下的问题便是:我们如何给出合适的dq电流参考值(
i
d
∗
,
i
q
∗
i_d^*,i_q^*
id∗,iq∗)从而控制有功功率和无功功率呢?
下面介绍母线电压控制和无功控制环的思路
根据式(4),我们知道,如果
i
d
i_d
id影响着逆变器的有功输出大小,因此如果母线电压较低时,我们就需要减小
i
d
i_d
id,这样逆变器的功率输出(
P
3
P_3
P3)就会减小,导致光伏和电池输出的能量之和大于逆变器的功率输出(
P
3
P_3
P3),进而可以对电容进行充电也就提高了电容的电压。相反,母线电压低于参考值时,我们就应该提高
i
d
i_d
id。
母线电压
U
U
U的变化可以用如下公式近似表示:
d
d
t
(
1
2
C
U
2
)
=
C
U
d
U
d
t
=
3
2
e
d
i
d
−
P
∗
(
10
)
frac{d}{dt}(frac{1}{2}CU^2)=CUfrac{dU}{dt}=frac{3}{2}e_di_d-P^*(10)
dtd(21CU2)=CUdtdU=23edid−P∗(10)其中,
P
∗
P^*
P∗表示系统所要求的有功处理。显然,这里做了一个假设:光伏的有功输出和电池的有功输出之和已经接近系统所要求的有功出力要求。我们进一步假设
U
U
U已经接近设定的母线电压值
U
b
u
s
U_{bus}
Ubus。式(10)可以近似线性化为:
C
U
b
u
s
d
U
d
t
=
3
2
e
d
i
d
−
P
∗
(
11
)
CU_{bus}frac{dU}{dt}=frac{3}{2}e_di_d-P^*(11)
CUbusdtdU=23edid−P∗(11)其中,
C
C
C为母线电容容值。
对线性化的式(11)进行Laplace变换,我们可以得到:
s
U
=
3
2
C
U
e
d
(
i
d
−
2
3
e
d
P
r
e
f
)
(
12
)
sU=frac{3}{2CU}e_d(i_d-frac{2}{3e_d}P_{ref}) (12)
sU=2CU3ed(id−3ed2Pref)(12)
此时,
i
d
i_d
id是我们的控制变量(请注意,借助电流环,我们可以控制
i
d
i_d
id为我们的设定值,因此可以将它看作控制变量,也就是电流环是内环)。令
i
d
i_d
id为如下形式:
i
d
=
(
K
p
+
K
i
/
s
)
(
U
−
U
r
e
f
)
+
2
3
e
d
P
r
e
f
(
13
)
i_d=(K_p+K_i/s)(U-U_{ref})+frac{2}{3e_d}P_{ref}(13)
id=(Kp+Ki/s)(U−Uref)+3ed2Pref(13)
将(13)代入(12),我们可以得到如下系统:
U
=
C
0
K
p
s
+
C
0
K
i
s
2
+
C
0
K
p
s
+
C
0
K
i
U
r
e
f
(
14
)
U=frac{C_0K_ps+C_0K_i}{s^2+C_0K_ps+C_0K_i}U_{ref}(14)
U=s2+C0Kps+C0KiC0Kps+C0KiUref(14)其中,
C
0
=
3
e
d
2
U
b
u
s
C
=
3
×
220
2
2
×
750
×
C
C_0=frac{3e_d}{2U_{bus}C}=frac{3times 220sqrt{2}}{2times 750times C}
C0=2UbusC3ed=2×750×C3×2202
类似于电流环的控制分析,我们可以知道式(14)代表,母线电压最终会趋向于
U
r
e
f
U_{ref}
Uref。PI参数的配置方法和电流环的配置是类似的:
{
ξ
=
1
2
C
0
K
i
K
p
=
0.8
ω
n
=
C
0
K
i
=
3
ξ
t
r
t
r
=
0.05
(
15
)
left{ begin{array}{c} xi = frac{1}{2}sqrt{frac{C_0}{K_i}}K_p=0.8\ omega_n=sqrt{C_0K_i}=frac{3}{xi t_r}\ t_r = 0.05 end{array} right. (15)
⎩⎪⎨⎪⎧ξ=21KiC0Kp=0.8ωn=C0Ki=ξtr3tr=0.05(15)
这里我们希望外环的收敛速度更慢。这是因为我们假设了对于外环来说,内环的控制速度是最够快的。
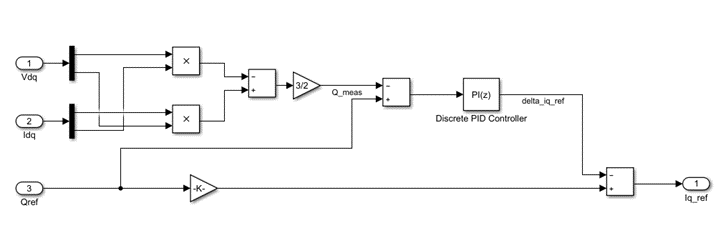
无功控制环,的配置就不再赘述了。这里只给出其控制框图:
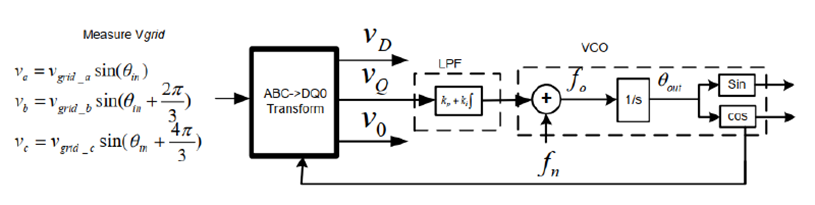
逆变器控制的最后内容!——锁相环
显然,我们上面的分析都用到了dq值。那么我们该怎么得到dq值呢?现实中,我们只能测量得到三相的电流或者电压,因此我们需要一个器件得到dq值。这个器件就是锁相环。
我们希望park变换后,电网侧的电压的q轴电压为零,因此,我们输入的就是电网侧的三相电压。锁相环的具体原理见下图。
剩下的部分见part2。
最后
以上就是包容歌曲最近收集整理的关于光伏-储能并网系统仿真(MATLAB/SIMULINK)-part1光伏-储能并网系统仿真(MATLAB/SIMULINK)-part1的全部内容,更多相关光伏-储能并网系统仿真(MATLAB/SIMULINK)-part1光伏-储能并网系统仿真(MATLAB/SIMULINK)-part1内容请搜索靠谱客的其他文章。








发表评论 取消回复