ezphysics.nchu.edu.tw/prophys/ael/File/Datasheet/Current-feeback2.pdf

Introduction 

Current feedback amplifiers (CFA) have sacrificed the dc precision of voltage feedback amplifiers (VFA) for speed. This tradeoff results in higher bandwidth that is relatively independent of closed loop gain and faster slew rate. Although CFAs do not have the precision of their VFA counterparts, they are precise enough to be dc coupled in video applications without sacrificing much dynamic range. CFAs have eliminated the ac coupling requirement that existed in previous high frequency amplifier designs; they operate in the GHz range while dc coupled. CFAs have much faster slew rates than VFAs, so they have faster rise/fall times and less intermodulation distortion. This application note assumes that the reader is familiar with feedback electronics and VFAs. Refer to Texas Instruments application note SLVA058 for basic feedback analysis tools. Texas Instruments application note SLOA020 covers VFA stability and theory.

The CFA model is shown in Figure 1. The noninverting input of a CFA connects to the input of a buffer (input buffer), so it has a very high impedance similar to a bipolar transistor VFA input. The inverting input connects to the input buffer’s output, so the inverting input impedance is very low. ZB models the input buffer’s output impedance, and it is usually less than 50 ohms. The buffer gain, GB, is as close to one as IC design methods can achieve, so it is neglected in the calculations.

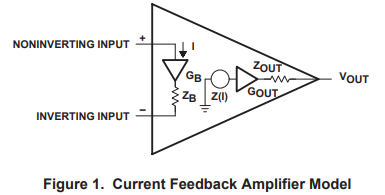
 The output buffer provides a low output impedance for the amplifier. Again, the output buffer gain, GOUT, is very close to one, so it is neglected in this analysis. The output impedance of the output buffer can be ignored except when driving very low impedance or capacitive loads. The input buffer’s output impedance can not be ignored because it affects stability at high frequencies.

The current-controlled current source, Z, is a transimpedance. The transimpedance in a CFA serves the same function as the gain in a VFA. Usually the transimpedance is very high, in the megohm range, so the CFA obtains accuracy by closing a feedback loop in a manner similar to the VFA.

Development of the Stability Equation

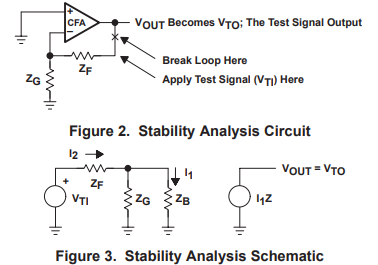
The stability equation is developed with the aid of Figure 2. Remember, stability is independent of the input, and stability depends solely on the loop gain (Aβ). The stability equation is developed by breaking the loop at point X, inserting a test signal (VTI), and calculating the return signal (VTO). The circuit shown in Figure 3 has the model substituted for the CFA symbol. The input buffer gain, the output buffer gain, and output buffer output impedance have been left out of the circuit to simplify calculations. This approximation is valid for almost all applications.

The Noninverting CFA 

 The closed loop gain equation for the noninverting CFA is developed with the aid of Figure 4 where external gain setting resistors have been added. The buffers are shown in Figure 4, but because their gains equal one, they do not enter into the calculations.

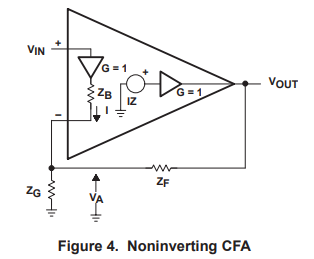
When the transimpedance (Z), is very high the term ZF/Z in equation 10 approaches zero, and equation 10 reduces to equation 11 which is the ideal closed loop gain equation for the CFA. The ideal closed loop gain equations for the noninverting CFA and VFA op amps are identical, and the degree to which they depart from ideal is dependent on the validity of the assumptions. The VFA has one assumption: the direct gain is very high; while the CFA has two assumptions: the transimpedance is very high and the input buffer output impedance is very low. As would be expected, two assumptions are harder to meet than one; thus the CFA departs from the ideal more than the VFA does.

The Inverting CFA 

The inverting CFA configuration is seldom used because the input impedance is very low (ZB||ZF +ZG). When ZG is selected as a high resistance to swamp out the effects of ZB, ZF must also be high to achieve at least unity gain. High values for ZF result in poor bandwidth performance as seen in the next section. If ZG is selected as a low value, ZB, which is frequency sensitive, causes the gain to increase as frequency increases. These limitations restrict the applications of the inverting CFA.

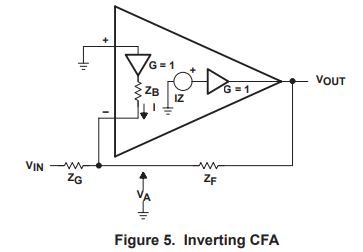
 The current equation for the input node is written as equation 12. Equation 13 defines the dummy variable (VA) and equation 14 is the transfer equation for the CFA. These equations are combined and simplified leading to equation 15, which is the closed loop gain equation for the inverting CFA.

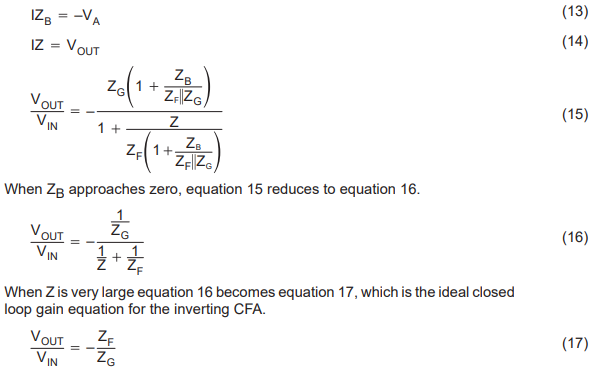
 The ideal closed loop gain equations for the inverting VFA and CFA op amps are identical. Both configurations have lower input impedance than the noninverting configuration has, but the VFA has one assumption while the CFA has two assumptions. Again, as was the case with the noninverting counterparts, the CFA is less ideal than the VFA because of the two assumptions. The zero ZB assumption always breaks down in bipolar-junction transistors, as is shown later. The differential amplifier configuration is almost never used with CFAs because of the gross input impedance mismatch.

Stability Analysis

Comparing equations 9 and 15 to equation 18 shows that the inverting and noninverting CFA op amps have identical stability equations. This confirms the earlier statement that the op amp input has no bearing on stability. The two op amp parameters affecting stability are the transimpedance (Z) and the input buffer’s output impedance (ZB). The external components affecting stability are ZG and ZF. The external impedances are controlled by the designer, although stray capacitance, which is a part of the external impedance, sometimes appears uncontrollable. Z and ZB are CFA op amp parameters, and they cannot be controlled by the circuit designer, so the designer must deal with them. We take the log of equation 18 prior to plotting the logs (equations 19 and 20) in Figure 6. 

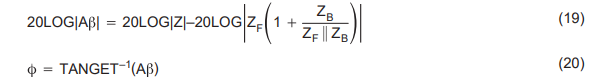
The log plot, called a Bode plot, is named after H. W. Bode, who first developed it in the forties. It enables the designer to add and subtract components of the stability equation graphically. 

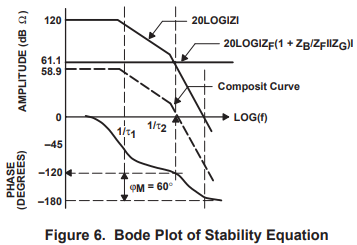
The transimpedance has two poles, and the plot shows that the op amp will be unstable without the addition of external components because 20LOG|Z| crosses the 0 dB axis after the phase shift equals 180°. The external components reduce the loop gain 61.1 dB, so the circuit is stable because it has 60° phase margin. Notice that the parallel combination of ZF and ZG contribute little to the phase margin because ZB is so small.

When ZB = 0 Ω and ZF = RF the loop gain equation is; Aβ = Z/RF. Under these conditions, stability is determined by Z and RF, and a value of RF can always be found to stabilize the circuit. The transimpedance and feedback resistor have a major impact on stability, and the input buffer’s output impedance has a minor effect on stability. Since ZB increases with an increase in frequency, it tends to increase stability at higher frequencies. Equation 18 is rewritten as equation 24, but is has been manipulated so that the ideal closed loop gain is readily apparent.

The closed loop ideal gain equation (inverting and noninverting) shows up in the denominator of equation 24, thus the closed loop gain influences the stability of the op amp. When ZB approaches zero the closed loop gain term also approaches zero, and the op amp becomes independent of the ideal closed loop gain. Under these conditions, RF determines stability, and the bandwidth is independent of the closed loop gain. Many people claim that the CFA bandwidth is independent of the closed loop gain, and that claim’s validity is dependent on the ratio of ZB/ZF being very low. 

ZB is important enough to warrant further investigation, so the equation for ZB is given in equation 25.

At low frequencies hib = 50 Ω and RB/(β0+1) = 25 Ω, so ZB = 75 Ω. ZB varies in accordance with equation 25 at high frequencies. The transistor parameters in equation 25 vary with transistor type, and these parameters are different for NPN and PNP transistors, thus ZB is also dependent on the output polarity. ZB is a small factor in the equation, but it adds a lot of variability to the current feedback op amp.

Stability and Input Capacitance 

When stray capacitance forms on the inverting input node to ground, it causes the impedance ZG to become reactive. The stability equation for this situation is given below.

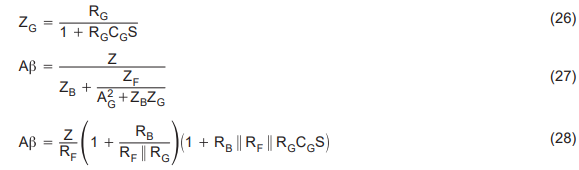
 Equation 28 is the stability equation when ZF is resistive, and there is stray capacitance between the inverting input node and ground. The stray capacitance, CG, remains a fixed value because it is dependent on the circuit layout. The pole created by the stray capacitance is dependent on RB because it dominates RF and RG. In addition, RB fluctuates with manufacturing tolerances. As the RBCG combination becomes larger, the pole moves towards the zero frequency axis. Eventually it interacts with the pole contained in Z, 1/τ2, and instability results.

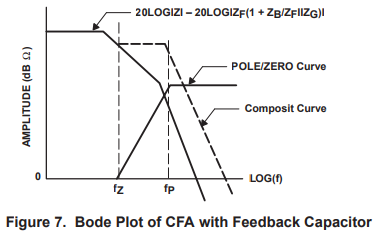
Stability and Feedback Capacitance

 This loop gain transfer function contains a pole and zero, thus, depending on the pole/zero placement, oscillation can result. The Bode plot for this case is shown in Figure 7. The original and composite curves cross the 0 dB axis with a slope of –40 dB/decade, so either curve can indicate instability. The composite curve crosses the 0 dB axis at a higher frequency than the original curve; hence, the stray capacitance has added more phase shift to the system. The composite curve is surely less stable than the original curve. Adding capacitance to the inverting input node or across the feedback resistor usually results in instability.

 Compensation of CF and CG

RB is an IC parameter, so it is dependent on the IC process. RB it is an important IC parameter, but it is not important enough to be monitored as a control variable during the manufacturing process. RB has widely spread, unspecified parameters, thus depending on RB for compensation is risky.

Selection of the Feedback Resistor

 The feedback resistor determines stability and it has an effect on closed loop bandwidth, so it must be selected very carefully. Most CFA IC manufacturers employ applications and product engineers who spend a great deal of time and effort selecting RF. They measure each closed loop gain with several different feedback resistor values to gather data. Then they pick a compromise value of RF that yields stable operation with low peaking, and that value of RF is recommended on the data sheet for that specific gain. Generally this is done for several different gains in anticipation of the various gains their customer applications require (often G=1, 2, or 5).

When the circuit designer strays from the RF value recommended on the data sheet, he gets into stability or low bandwidth problems. Lowering RF decreases stability, and increasing RF decreases bandwidth. What happens when the designer needs to operate at a gain not specified on the data sheet? The designer must select a new value of RF for the new gain. Assume that (Aβ)1 for a gain of one equals (Aβ)N for a gain of N, and that there is a linear relationship between stability and gain.

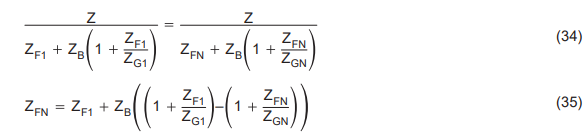
 Equation 35 leads one to believe that a new value for ZF can easily be chosen for each new gain. This is not the case in the real world; the assumptions don’t hold up good enough to rely on them. When you change to a new gain not specified on the data sheet, equation 35 supplies a starting point for RF, but you must test to determine the final value of RF.

CFAs Versus VFAs

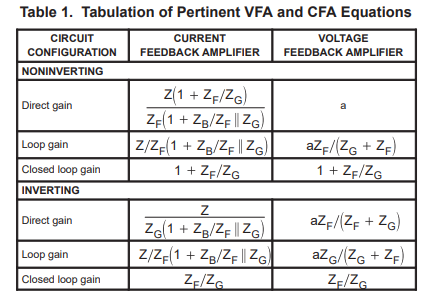
The equations for the CFA and the VFA are given in Table 1. The closed loop gain for both op amps is identical, but the remaining equations are different. This situation leads to the natural conclusion that ideal closed loop performance is identical as long as the approximations remain true. The approximations are true for frequencies much lower than the advertised –3 dB frequency, but they fall apart at the –3 dB frequency. Both types of op amps have particular niche markets.

VFAs dominate the precision and low voltage/low power markets. VFAs dominate the precision market because their differential amplifier input structure enables them to employ matching to eliminate offset voltages and currents. VFAs dominant the low voltage/power market because their circuit configuration enables them to operate in a rail-to-rail mode. VFAs have poor slew rate, and this limits their pulse handling capability.

CFAs have much higher bandwidth because the have much lower impedances in the inverting input circuit and the feedback circuit. The bandwidth stays high longer in CFAs; thus, a 50 MHz CFA is usable at much higher frequencies than a 50 MHz VFA. The CFA circuit topology enables them to supply slew current from the output structure; thus, they have much faster slew rates. The CFAs stability is determined by the value of the feedback resistor.

 Summary

The CFA is not limited by constant gain-bandwidth criteria, so the feedback resistor is adjusted for maximum performance. The stability is dependent on the feedback resistor; as RF is decreased stability is decreased, and when RF goes to zero, the circuit becomes unstable. As RF is increased stability increases, but the bandwidth decreases.

The inverting input impedance is very high, but the noninverting input impedance is very low. This situation precludes CFAs from operation in the differential amplifier configuration. Stray capacitance on the inverting input node or across the feedback resistor always leads to peaking, usually to ringing, and sometimes to oscillations. A prudent circuit designer scans the PC board layout for stray capacitances and eliminates them. Breadboarding and lab testing are necessary with CFAs. The CFA performance can be improved immeasurably with a good layout,  good decoupling capacitors, and low inductance components.

Other reference

 Feedback Amplifiers Theory and Design         by Gaetano Palumbo University of Catania

 feedback.pdf (kmutnb.ac.th)

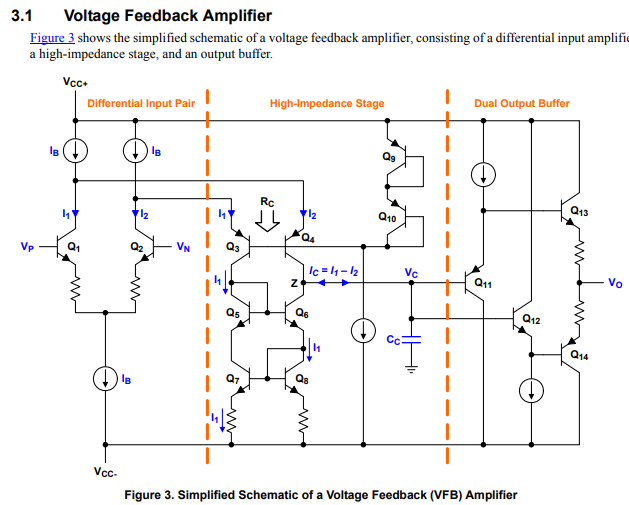
Voltage Feedback versus Current Feedback Operational Amplifiers

https://www.renesas.com/us/en/document/apn/an1993-voltage-feedback-versus-current-feedback-operational-amplifiers?language=en 

To summarize, the major difference between a VFB and a CFB amplifier is the type of input error signal generating the output voltage. A VFB op-amp uses an error voltage while a CFB op-amp uses an error current. 

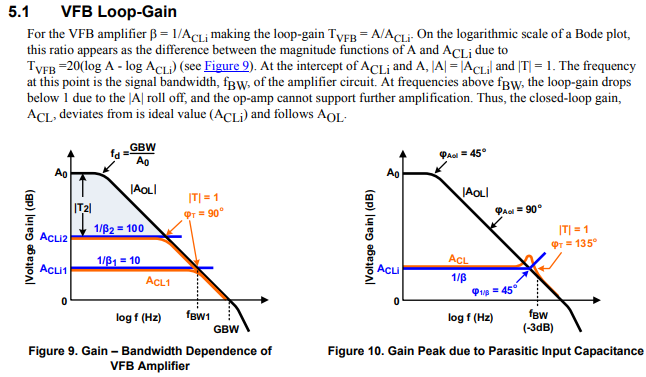
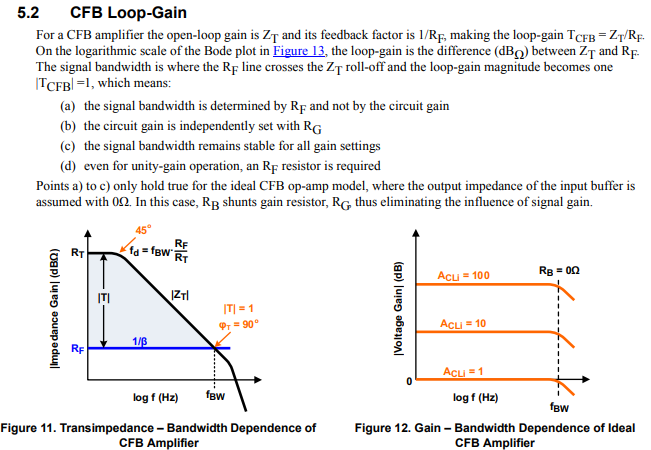
"Feedback Amplifier Analysis Tools"

https://linearaudio.nl/sites/linearaudio.net/files/fb%20amp%20analysis%20tools%20sloa017a_0.pdf

2 Block Diagram Math and Manipulations

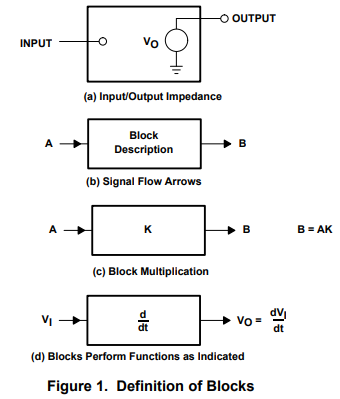
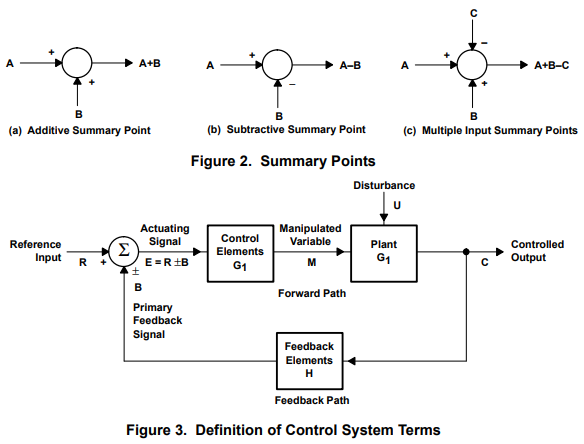
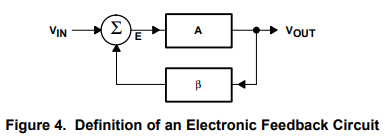
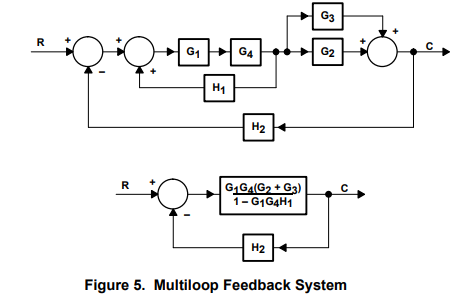
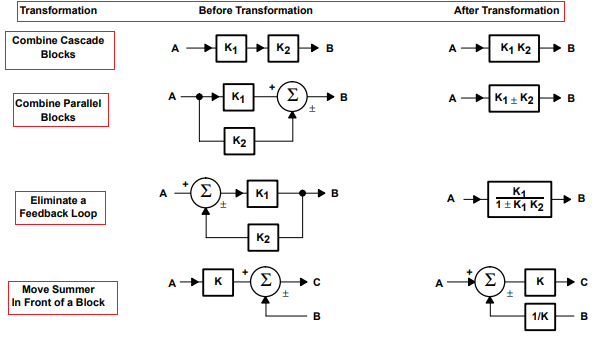
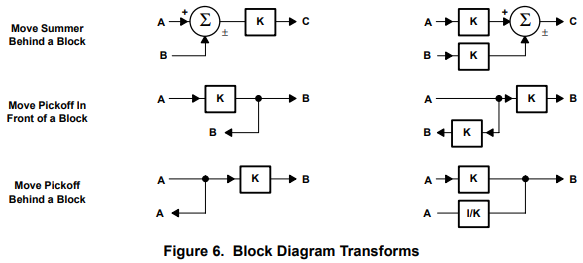
Block diagram reduction rules:

• Combine cascade blocks

• Combine parallel blocks

• Eliminate interior feedback loops

• Shift summing points to the left

• Shift takeoff points to the right

• Repeat until canonical form is obtained 

Figure 6 gives the block diagram transforms. The idea is to reduce the diagram to its canonical form because the canonical-feedback loop is the simplest form of a feedback loop, and its analysis is well documented. All feedback systems can be reduced to the canonical form, so all feedback systems can be analyzed with the same math. A canonical loop exists for each input to a feedback system; although the stability dynamics are independent of the input, the output results are input dependent. The response of each input of a multiple-input feedback system can be analyzed separately and added through superposition.

最后

以上就是爱撒娇凉面为你收集整理的Current Feedback Amplifier Analysis and CompensationIntroduction Development of the Stability EquationThe Noninverting CFA The Inverting CFA Stability AnalysisStability and Input Capacitance Stability and Feedback Capacitance Compensation of CF and C的全部内容，希望文章能够帮你解决Current Feedback Amplifier Analysis and CompensationIntroduction Development of the Stability EquationThe Noninverting CFA The Inverting CFA Stability AnalysisStability and Input Capacitance Stability and Feedback Capacitance Compensation of CF and C所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。