MATLAB中BPSK的星座图仿真

  第一次写博客，肯定写不好，但是希望记录一下自己学习的过程，多多担待。
  学习无线通信，要做BPSK的星座图仿真实验，网上搜了一下，没人发资料，我就记录一下自己的过程。过两天还做16QAM的仿真，有时间再写那个的，如果我会做那个的话。
由于需要插入一些表达式，如果不会的同学，可以参考这里的链接，Markdowm公式指导手册，里面也有简明教程的链接，点过去，可以学习的。
切入正题，标题MATLAB中BPSK的星座图仿真。

一.星座图

  BPSK是怎么扯到了星座图的,来,看公式
$$e_{2psk}(t)=\{\begin{array}{ll}Acos{w}_{c}t,& \text{发送码元“1”}\\ -Acos{w}_{c}t,& \text{发送码元“0”}\end{array}$$
我们知道$sin{w}_{c}t和cos{w}_c$是正交的，可以作为信号空间的两个基，就像X轴和Y轴，可以表示任意的二维信号，这个从傅里叶级数可以看出。
 现在在以$sin(w_{c}t)和cos(w_{c}t)$为基的信号空间中，码元1的坐标为（A，0），码元0的坐标为（-A，0）那么还有噪声呢，它的坐标呢，如果你看过通信原理的书，就会知道经过带通滤波器的噪声信号为
$$\xi (t)={\xi }_c(t)cos{w}_{c}t-{\xi }_c(t)sin{w}_{c}t$$
所以噪声的坐标为${\xi }_c(t)$,它的均值为零，方差为$\sigma$，这个的产生要用函数randn( )产生。
 星座图为我们理解调制解调信号提供了新的角度，仅从坐标图就可看出信号的能量，两个信号的距离，非常好用的。
 现在给matlab的代码，

%运行时间略微有些长，
clc,clear
%比特流的长度，不要太大，容易死机
Maxbit = 1000000;
Eb = 1;
for i=1:15                        % 信噪比从1到15dB
  for cnt=1:10              	  %对于每个信噪比，进行10次实验，最后求平均 
       b = rand(1,Maxbit);         %随机数据
       b_bin = round(b);            % 0 1 比特流      
       b2 = sign(b_bin - 0.5);     %调制后的 -1 和+1 比特流
      SNR = 10 ^( 0.1 * i);           %信噪比
      N0 = Eb/SNR;
      Sigma = sqrt(N0/2);
      % 高斯噪声信号，注意用的函数是randn,而不是rand
      Noise = Sigma*randn(1,Maxbit);
      % snt 调制信号与噪声叠加后的信号
      Snt = b2 + Noise;
      % 解调过程，抽样判决，<0,判为-1，>0,判为+1
      res(Snt<0) = -1;
      res(Snt>=0) = 1;
      % Snt .* b2，解调正确，相乘结果为+1，若发生误码，结果为-1
      St = res .* b2;
      % err为误码的个数
      err(cnt) = length(find(St<0));
  end
  % Pb计算信噪比为 i dB 时的误比特率
  Pb(i) = (mean(err)/Maxbit)*100;
end
%打印误码率,注意这个函数
semilogy(Pb); 
xlabel('信噪比(dB)');
ylabel('误码率Pe')

我想说啥呢，就是最后打印误码率的函数，我开始用的是plot( ),就是下图

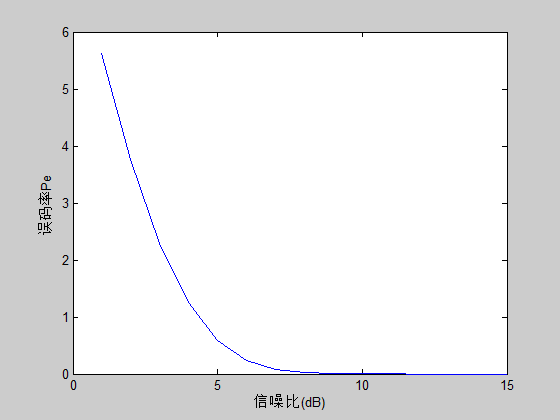
跟书上不一样，后来我发现他们跟书上一样的，用的是semilogy( ) 函数，然后图就是这个了。

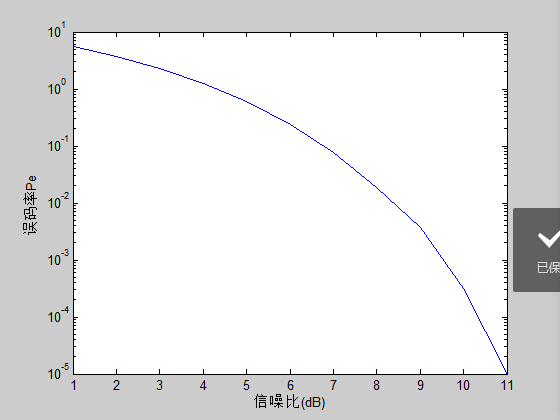
semilogy（）的纵轴坐标是$10^i$,看到了吧，就是这样的。
 到这里，说完了。
 第一次写，用了老长时间呢,顺便学了Markdown的用法，还有呢，matlab也是老长时间没用过了，老多函数都忘了，还有啊，BPSK的星座图也不大会，一切都是昨天下午临时干的，最耗时就是找出semilogy( )这个函数，花了4个小时呢，真实的，浪费时间啊。

最后

以上就是甜蜜战斗机为你收集整理的MATLAB中BPSK的星座图仿真的全部内容，希望文章能够帮你解决MATLAB中BPSK的星座图仿真所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。