串联校正之超前校正

“无源超前校正”和“有源超前校正”的电路构造

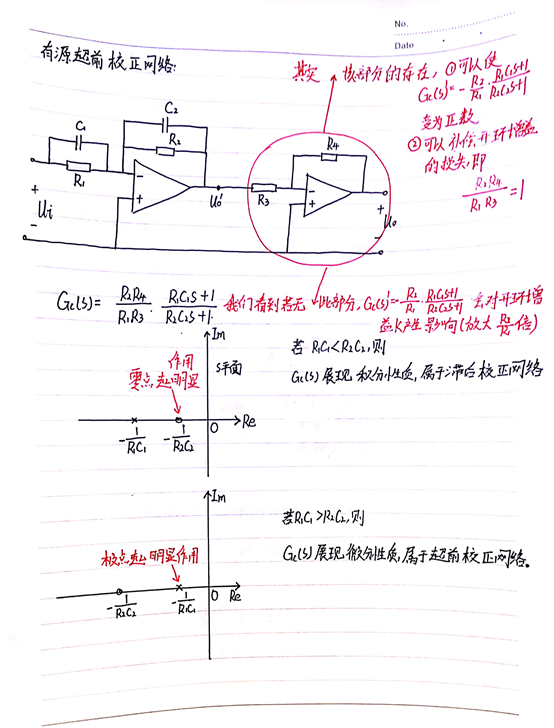
超前校正的实质

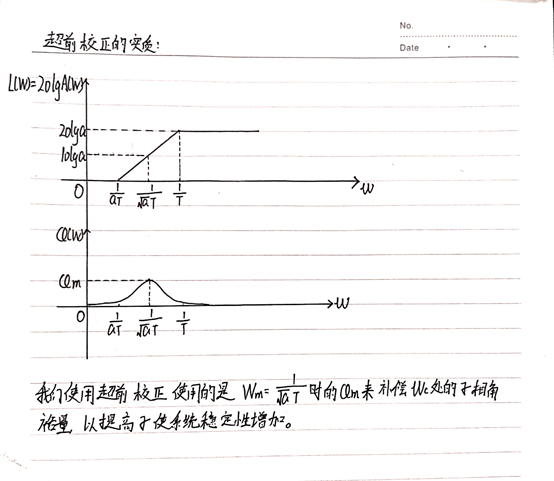
而且，超前校正可以提高截止频率Wc，使得系统的响应速度和超调量得到改善(Wc升高会造成系统响应速度ts缩短，超调量σ%减小，有利于系统的稳定性)。

注意：稳态性能和稳定性不太一样，我们看稳态性能的时候一般看系统的稳态误差ess，而看系统稳定性时，我们一般看系统的超调量σ%和系统的谐振峰值Mr。

超前校正的步骤

例题：

① 根据题目中给出的稳态误差求出开环增益K，进而可以绘制出Bode波特图，求出频率特性，即根据如下表达式进行绘图操作：

② 求出开环截止频率ωc，以及ω=ωc时的幅角和相角裕度γ

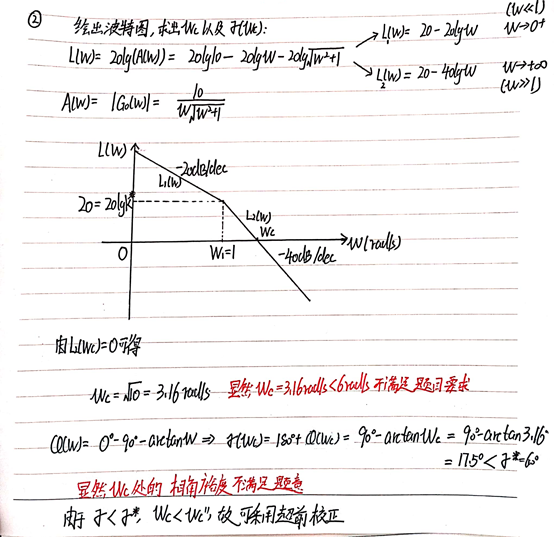
③ 根据题目中要求的相角裕度求出用所需的最大超前量∆∅=∅m，最大超前量都出来了，我们进而可以求解以下式子中的参数：

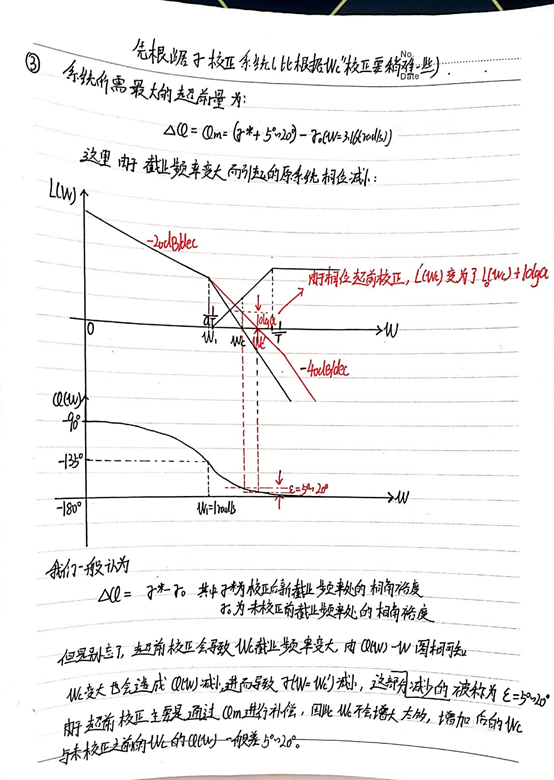
我们要使得补偿后，γ相角裕度满足题意，必须把“因为截止频率变大而造成的相角损失”考虑在内，作为补偿的一部分。

由公式：

得，

其中，Wc附近整体向上抬升10lg(a)，即

④ 根据求出来的α，我们可以求解出新的截止频率：

由上述公式，我们可以求出“按照γ相角裕度校正后得到的截止频率Wc‘“为：

但是，我们发现我们按照γ相角裕度校正后得到的截止频率Wc‘并不符合题意：

⑤ 将求解出来的ωc‘与我们题目中要求的截止频率ωc‘’进行比较，取最终的截止频率为

若，即我们最终求的截止频率不符合要求，那么我们选择题目中的ωc‘’作为我们新的校正后的截止频率；

根据我们按照γ相角裕度校正后得到的截止频率Wc‘与题目中要求的截止频率Wc‘’做对比，我们可以得知：

⑥ 根据新的截止频率求出新的α，以及时间常数Ta；

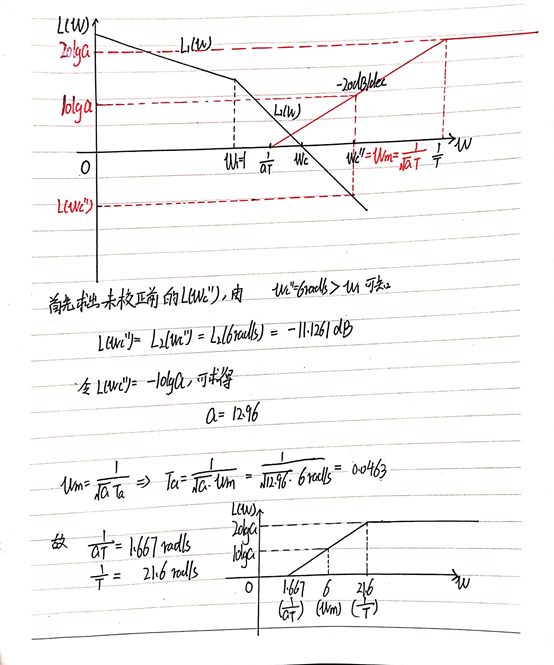
⑦ 根据最终得到的结果计算出截止频率ωc‘’处的相角裕度，看看是否符合题意，若有其他要求的参数，比如“幅值裕度”，一般来说按照如上的7个步骤最终计算出来的结果一般符合题意，若不符合题意，可以适当的加大一点截止频率进行计算。

上述网络校正结果如下：

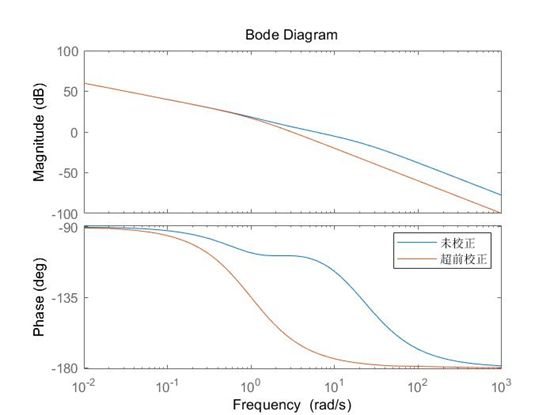
超前校正网络的适用领域

① 首先，我们要明确超前校正网络的实质：充分利用中频段自身相角超前的特性来补偿未校正网络的W=Wc(截止频率)处的相角裕度，同时由于自身在中频段产生的幅频特性为正值，超前校正可以在小范围内提高截止频率，使得校正后网络的截止频率大于未校正前网络的截止频率，举个例子：

在上述题目中，未校正前网络的截止频率为Wc=3.16rad/s，校正后网络截止频率为Wc’’=6rad/s，只是适当的提高了Wc，并没有一下子提高10~20rad/s，这是由于超前校正网络的性质导致的，就相当于超前校正网络的主要功能是“通过自身的超前相角来给系统提供超前量”，辅助功能是“利用自己可以提高Wc截止频率的特性来改善系统的快速性与稳定性”。

② 给系统提供超前量得有个上限，就是当系统的相角在W=Wc附近时，出现断崖式下跌，那超前校正网络显然力不从心，虽然我们有时候小概率可能通过多个矫正网络的串联来使得网络勉强达到题目要求，但是这样的系统极其不稳定，频率稍稍一变，马上就不符合题意了。

③ 当题目中要求提高相角裕度的同时，缩小截止频率，“缩小”显然和超前校正网络的“提高Wc截止频率“的特性相悖，此时超前校正网络不适用。

Matlab查看稳定裕度

未校正前网络参数

未校正前系统的开环传递函数(默认反馈传递函数为1)

幅值裕度Gm,相角裕度Pm,幅值穿越频率Wcg,相角穿越频率Wcp

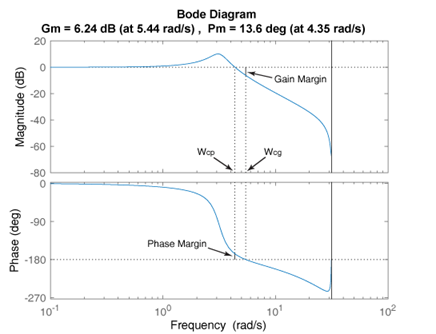
进行超前校正后系统的开环传递函数(默认反馈传递函数为1)

幅值裕度Gm,相角裕度Pm,幅值穿越频率Wcg,相角穿越频率Wcp

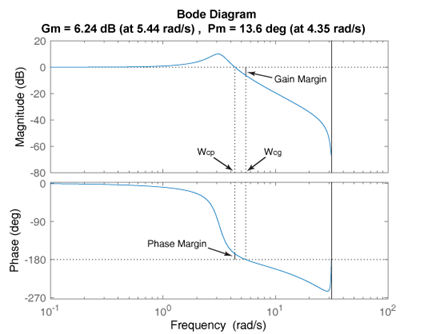
最后

以上就是谦让草丛为你收集整理的线性系统的频域分析与校正之超前校正网络（原理+分析）串联校正之超前校正的全部内容，希望文章能够帮你解决线性系统的频域分析与校正之超前校正网络（原理+分析）串联校正之超前校正所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。